适合普及/提高阶段:代码部落2026年1月月赛Level 2真题解析

31 37 83 4

5

51 12 23 34 45 5

5

109 2537 3810 115 199 2018 2332 416 1511 3335 41

30

#include<bits/stdc++.h>usingnamespace std;structpoint{longlong st, ed, len;}a[500005];int n;longlong f[500005];boolcmp(point x, point y){return x.ed < y.ed;    }intbinary(int l, int r, longlong x){ int ans = 0;while(l <= r)    {int mid = (l + r) >> 1;if(a[mid].ed < x) ans = mid, l = mid + 1;else r = mid - 1;    }return ans;}intmain(){    cin >> n;for(int i = 1; i <= n; i++)    {           cin >> a[i].st >> a[i].ed;        a[i].len = a[i].ed - a[i].st + 1;    }sort(a + 1, a + n + 1, cmp);for(int i = 1; i <= n; i++)    {int k = binary(1, i - 1, a[i].st);        f[i] = max(f[i - 1], f[k] + a[i].len);    }    cout << f[n];}

24N 1E 1S 1W 121W 1N 1W 1N 1W 1N 3E 1N 1E 1S 1E 2N 1E 1S 1E 1S 3W 1S 1W 1S 1W 1

41

15N 2E 1E 1S 2W 2

4

对于样例一 Case #1：

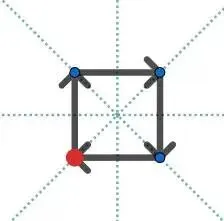
对于样例一 Case #2：

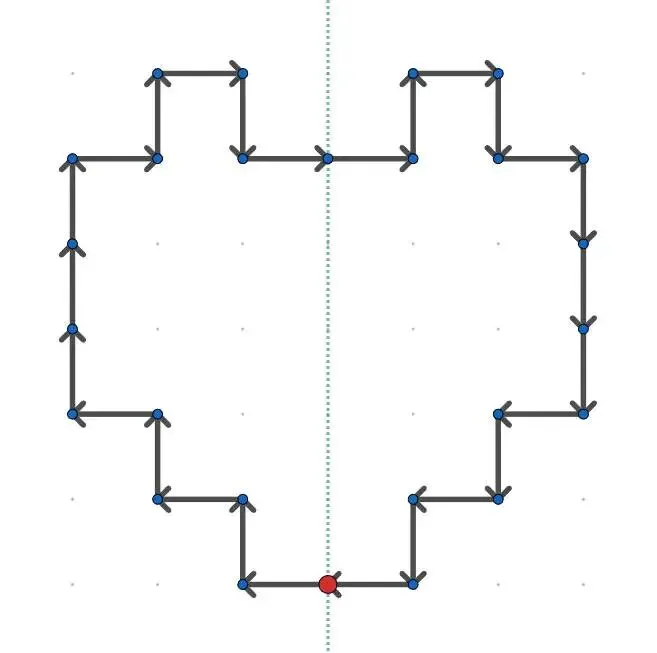
对于样例二：

请注意有可能前后两条指令的方向相同。

对于大样例：

缩放后的形状类似于一个中心对称的菱形结构，共四条对称轴：

 /\/  \\  / \/

题解

图形的轴对称性可转化为「特征序列的回文性」—— 若图形存在某条对称轴，则沿该轴折叠后，两侧的“步数+转向”信息完全对称

1. 预处理指令：合并连续同方向指令，减少冗余，比如N1E1E1S1S1W1W1N1合并为N2E2S2W2（首尾也要考虑合并）
2. 构建特征序列：将“步数+转向”作为基本单元，形成描述图形形状的环状序列；
3. 环转链处理：将环状序列复制为线性序列（），方便用线性方法判断环状回文；
4. 哈希回文判断：用前缀哈希+后缀哈希快速验证序列是否回文，统计有效对称轴数量。

#include<bits/stdc++.h>usingnamespace std;typedefunsignedlonglong ull;unordered_map<char, int> dir = {    {'N', 0},    {'E', 1},    {'S', 2},    {'W', 3}};// 左转 3、直行 0、右转 1、回退 2intturn(char pre, char nxt){return (dir[nxt] - dir[pre] + 4) % 4;}char d[400005]; // 方向int s[400005];  // 步数int arr[1600005], tot;// 自然溢出法，哈希常量const ull chsh = 1e9 + 7;// 前缀哈希、后缀哈希、哈希常量次方值ull hl[1600005], hr[1600005], pw[1600005];// 初始化 pwvoidinit(){    pw[0] = 1;for(int i = 1; i < 1600005; i++)        pw[i] = pw[i - 1] * chsh;}boolcheck(int l, int r){    ull x = hl[r] - hl[l - 1] * pw[r - l + 1];    ull y = hr[l] - hr[r + 1] * pw[r - l + 1];return x == y;}voidsolve(){int m, n = 0;    cin >> m;for(int i = 0; i < m; i++)    {char x;int y;        cin >> x >> y;if(i == 0 || x != d[n - 1])        {            d[n] = x;            s[n] = y;            n++;        }else            s[n - 1] += y; // 合并共线情况    }if(d[0] == d[n - 1]) // 合并首尾共线情况    {        s[0] += s[n - 1];        n--;    }    tot = 0;for(int i = 0; i < n; i++)    {// 步数        arr[++tot] = s[i];// 方向变化（左转、右转、直行）        arr[++tot] = turn(d[i], d[(i + 1) % n]);    }// 化环为链for(int i = 1; i <= 2 * n; i++)        arr[++tot] = arr[i];    hl[0] = hr[tot + 1] = 0;for(int i = 1; i <= tot; i++)        hl[i] = hl[i - 1] * chsh + arr[i];for(int i = tot; i >= 1; i--)        hr[i] = hr[i + 1] * chsh + arr[i];int ans = 0;for(int i = 1; i <= 2 * n; i++)if(check(i, i + 2 * n ))            ans++;    cout << ans / 2 << "\n";}intmain(){init();int T;    cin >> T;while(T--)solve();return0;}

1610842-花开遍地

题目描述(Description)

江桥的花园可以看成是  行  列的网格，从上到下第  行，从左到右第  行的格子为 。每个格子里都有一朵花，有的花开了有的花没开，开了的用 * 表示，没开的用 . 表示。

称一片 花海 为：只包含已经开了的花朵的连通区域。这里的连通指的是四连通，即花海内任意一朵花朵都可以通过上下左右移动且只经过已经开了的花朵就可以到达花海内任意一个其他的开花的位置。

现在江桥可以使用恰好一次 “开花药水”，即选中某个格子  ，使得第  行和第  列的所有花朵开放。

现在有  次询问，每次询问给出 ，表示查询如果在  处使用 “开花药水”，所能形成的最大的花海的面积是多少（花海的面积即为花海所包含的花朵数目）。

输入格式(Format Input)

第一行三个正整数 ，表示花园的行数、列数、询问次数。

接下来  行每行一个长度为  的字符串 ，表示这一行的所有花朵的开花状态。

接下来  行，每行  个整数 x y，表示一组询问。

输出格式(Format Output)

 行每行一个非负整数，表示答案。

输入样例 1(Sample Input 1)

5 5 3......*.*..*.*.......*.*.1 12 24 3

输出样例 1(Sample Output 1)

141015

限制(Restrictions)

时间限制(Time Limit): 1000 ms内存限制(Memory Limit): 131072 KB

说明/提示

大样例分别对应子任务 、。

有合理的子任务依赖。

对于  的数据：保证 。

解析

每次查询指定位置，要求计算恰好将第行+第列所有格子变为开后，网格中最大四连通花海（仅含开的花）的面积。直接暴力模拟每个查询（修改行+列→找最大连通块）的时间复杂度为，而、，暴力会超时

优化：通过预处理将查询复杂度降至，核心是利用差分+前缀和快速计算操作后的花海面积。

操作后最大花海的面积由两部分组成：

1. 原始连通块贡献：所有与第行或第列相交的原始花海（连通块）的大小之和（记为）。

容斥原理求解sum

用BFS遍历所有原始连通块，记录每个块的行范围、列范围、大小。

那么能与这个块联通的行范围为、列范围

用差分数组预处理行/列维度的覆盖和，用前缀和快速计算任意对应的。

比如

表示行的差分数组，那就是

表示行的差分数组，那就是

容斥修正：通过**vc**数组记录列差分的反向更新，避免重复统计“行+列都覆盖”的块。

也就是每遍历一行，要把当前行 相关联的 列 进行 差分方向更新，从而在列的前缀和计算里去掉了行x且列y覆盖的块，见代码84~92行

1. 新增格子贡献：第行+第列中原本未开的格子数（需扣除重复计算的）。

时间复杂度

• BFS遍历连通块：
• 预处理数组：
• 查询：（每个查询）
• 总复杂度：，对于

#include<bits/stdc++.h>#define ll long long#define inf 0x3f3f3f3fusingnamespace std;constint N = 2e3 + 5;int n, m, k, mx;int a[N], belong[N][N], d[2][N];int ans, tmp, cnt;int flag;char s[N][N];int as[N][N];int num[2][N];int bj[4];int pre[N];int dx[] = {0, 1, 0, -1};int dy[] = {1, 0, -1, 0};structnode{int l;int r;int v;};vector<node> vc[N];voidbfs(int x, int y){    queue<pair<int,int> >q;    belong[x][y] = cnt;    bj[0] = bj[1] = x;    bj[2] = bj[3] = y;    q.push({x, y});int tot = 0;while(!q.empty())        {auto nd = q.front();q.pop();            tot++;for(int i = 0; i <= 3; i++)                {int tx = nd.first + dx[i];int ty = nd.second + dy[i];if(tx < 1 || tx > n || ty < 1 || ty > m ) continue;if(s[tx][ty] == '.') continue;if(belong[tx][ty]) continue;                    belong[tx][ty] = cnt;                    bj[0] = min(bj[0], tx);                    bj[1] = max(bj[1], tx);                    bj[2] = min(bj[2], ty);                    bj[3] = max(bj[3], ty);                    q.push({tx, ty});                }        }//维护单块最大值     mx = max(mx, tot);    d[0][bj[0] - 1] += tot;    d[0][bj[1] + 2] -= tot;    d[1][bj[2] - 1] += tot;    d[1][bj[3] + 2] -= tot;    vc[bj[0] - 1].push_back({bj[2] - 1, bj[3] + 2, -tot});    vc[bj[1] + 2].push_back({bj[2] - 1, bj[3] + 2, tot});}voidsolve(){    cin >> n >> m >> k; for(int i = 1; i <= n; i++)        {            cin >> s[i] + 1;for(int j = 1; j <= m; j++)                {if(s[i][j] == '*')                     {                        num[0][i]++;                        num[1][j]++;                    }                }        }for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)if(s[i][j] == '*' && !belong[i][j])                ++cnt, bfs(i, j);for(int i = 0; i <= n; i++)        {if(i) d[0][i] += d[0][i - 1];for(auto t : vc[i])                {                    d[1][t.l] += t.v;                    d[1][t.r] -= t.v;                }            pre[0] = d[1][0];for(int j = 1; j <= m; j++)                {                    pre[j] = pre[j - 1] + d[1][j];                    as[i][j] = d[0][i] + pre[j] + n + m - 1 - num[0][i] - num[1][j];if(i && s[i][j] == '*') as[i][j]++;                    as[i][j] = max(as[i][j],mx);                }        }for(int i = 1; i <= k; i++)        {int x, y;            cin >> x >> y;            cout << as[x][y] << '\n';        }}intmain(){    ios::sync_with_stdio(0);    cin.tie(0);    cout.tie(0); int T = 1, cas=1;while(T--) solve();return0;}

1610843-策略游戏

题目描述(Description)

江桥 和 小明 在玩一个策略游戏。

有一个长度为  的数组  和一个长度为  的数组 ，在此基础上定义一个大小为  的矩阵 ，满足  。所有下标均从  开始。

游戏一共会进行  轮，在每一轮中，会给出三个参数，格式如下：

op x y

如果 ，则这一轮会进行游戏（游戏轮），江桥必须从  中选择一个行号 ，然后小明再选择一个列号 ，那么这一轮中，两人的得分为 。然后， 在后面的游戏中就不能再被选中了（即江桥再选择  时，小明就不能选  了）。如果江桥选的第  行里没有可以选中的位置，则本轮不得分（即得  分）。

如果 ，则这一轮会进行修改（修改轮）， 的值会被修改为 ，对应矩阵的第  行中没有被选过的位置上的数字会随之发生变化。

江桥 的目标是使得分尽可能大，小明 的目标是使得分尽可能小。同时两人都是足够聪明的玩家，每次都会采用最优的策略。但是，两人无法预测后面的修改操作，因此两人每次进行游戏时都只会按照当前的最优策略进行。如果当前有多种选择都能获得同样的分数（包括  分），江桥会优先选择行号小的那个。

简言之：

① 如果江桥选的  行中有元素没选过，小明会优先选择没选过的列里   最小的那个（有多个则任选一个），如果得分为  ，满足”选取行号最小”原则。

② 如果江桥选的  行中已经没有可选元素，则得分为 ,同时与其他得分为  的行满足”选取行号最小”原则。

请问：按照二人的最优策略，每个游戏轮的得分是多少？

输入格式(Format Input)

第一行输入三个正整数 ，分别表示数组 ，数组  的长度和游戏轮数。

第二行： 个整数，表示 ，分别表示数组  的元素。

第三行： 个整数，表示 ，分别表示数组  的元素。

接下来  行，每行三个正整数 ，表示这一轮的信息。

如果 ，则表示游戏轮，江桥需要从  中选择一行。

如果 ，则表示修改轮， 的值会被修改为 。

输入保证至少有一个游戏轮。

输出格式(Format Output)

对于每个游戏轮，另起一行输出一个整数，表示这一轮游戏中，江桥 和 小明 在最优策略下的得分。

输入样例 1(Sample Input 1)

3 2 40 1 23 41 1 31 2 32 3 61 1 3

输出样例 1(Sample Output 1)

683

输入样例 2(Sample Input 2)

3 4 52 5 46 3 4 42 2 11 1 31 2 21 1 21 1 2

输出样例 2(Sample Output 2)

12368

限制(Restrictions)

时间限制(Time Limit): 1000 ms内存限制(Memory Limit): 131072 KB

说明/提示

在第一组样例中，最优的策略为：

 第一个游戏轮，江桥选择 ，小明选择 ，得分为 

 第二个游戏轮，江桥选择 ，小明选择 ，得分为 

 第一个修改轮， 被修改成了 ，但是第  行的所有数字都已经被选过了，故第  行后续再选的话得分只能为 

 第三个游戏轮，江桥选择 ，小明选择 ，得分为 

下发文件对应子任务 。

有合理的子任务依赖。

对于  的数据：保证 。输入保证至少有一个游戏轮。

题解

按  升序排序。

那么第一轮游戏的时候，小明肯定选择  最小的那一列，那么第一轮的得分为 

后面江桥再选这一行的时候，小明就只能选次小值。

因此，相当于每行的得分为  这一行没有被选过的最小的  。

直接开一颗线段树维护即可。注意边界情况。

总复杂度为 。

#include<bits/stdc++.h>#define ll long longusingnamespace std;constint N = 200010;int n, m, q;ll a[N], b[N], c[N];structtree{    ll mx;int pos; //最大值对应的行号 }tre[N << 2];voidupdate(int p){if(tre[p << 1].mx >= tre[p << 1 | 1].mx)        tre[p] = tre[p << 1];else        tre[p] = tre[p << 1 | 1];}voidbuild(int p, int l, int r){if(l == r)    {        tre[p].mx = a[l] * b[1];        tre[p].pos = l;return;    }int mid = (l + r) >> 1;build(p << 1, l, mid);build(p << 1 | 1, mid + 1, r);update(p);}voidupd(int p, int l, int r, int id, ll v){if(l == r)    {if(l == id) tre[p].mx = v, tre[p].pos = l;return;    }int mid = (l + r) >> 1;if(id <= mid)upd(p << 1, l, mid, id, v);elseupd(p << 1 | 1, mid + 1, r, id, v);update(p);}intqry(int p, int l, int r, int tl, int tr){if(l >= tl && r <= tr)return p;int mid = (l + r) >> 1;int p1, p2;    p1 = p2 = 0;if(tl <= mid)        p1 = qry(p << 1, l, mid, tl, tr);if(tr > mid)        p2 = qry(p << 1 | 1, mid + 1, r, tl, tr);if(p1 && !p2) return p1;elseif(!p1 && p2) return p2;else    {if(tre[p1].mx >= tre[p2].mx) return p1;elsereturn p2;    }}intmain(){    cin >> n >> m >> q; for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= m; i++) cin >> b[i];sort(b + 1, b + 1 + m);for(int i = 1; i <= n; i++) c[i] = 1;build(1, 1, n);while(q--)    {int op, x, y;        cin >> op >> x >> y;if(op == 1)        {int p = qry(1, 1, n, x, y);int id = tre[p].pos;            ll ans = tre[p].mx;            c[id]++;if(c[id] <= m) upd(1, 1, n, id, a[id] * b[c[id]]);elseupd(1, 1, n, id, 0);            cout << max(ans, 0ll) << '\n';        }else        {            a[x] = y;if(c[x] <= m) upd(1, 1, n, x, a[x] * b[c[x]]);        }     }return0;}