Python 生成金融数据相关矩阵
- 2026-01-04 19:33:00
在上一篇文章《生成具有真实相关结构的合成股票数据》中,我们探讨了如何构建具有结构化的合成相关矩阵,以生成具有相关性的合成股票数据。这类数据在系统化交易的回测验证和机器学习模型训练中具有多种用途。我们在“后续步骤”一节中提到,将探索开发一个更高级的工具,用于生成更大规模、既合成又高度逼真的金融时间序列数据。
在本文中,我们将构建这一更大型工具的第一个组成部分——一个基于面向对象编程的 Python 框架,用于生成合成资产价格序列。具体而言,我们将设计一个类层次结构,以支持多种数学模型来生成合成相关矩阵,这些模型在复杂度和真实感上逐步提升。所生成的相关矩阵实例将作为基础,用于进一步生成具有相关性的资产价格时间序列,从而模拟金融市场中存在的一些“典型事实”(stylized facts)。
作为先行预览,我们将生成如下所示的相关矩阵:
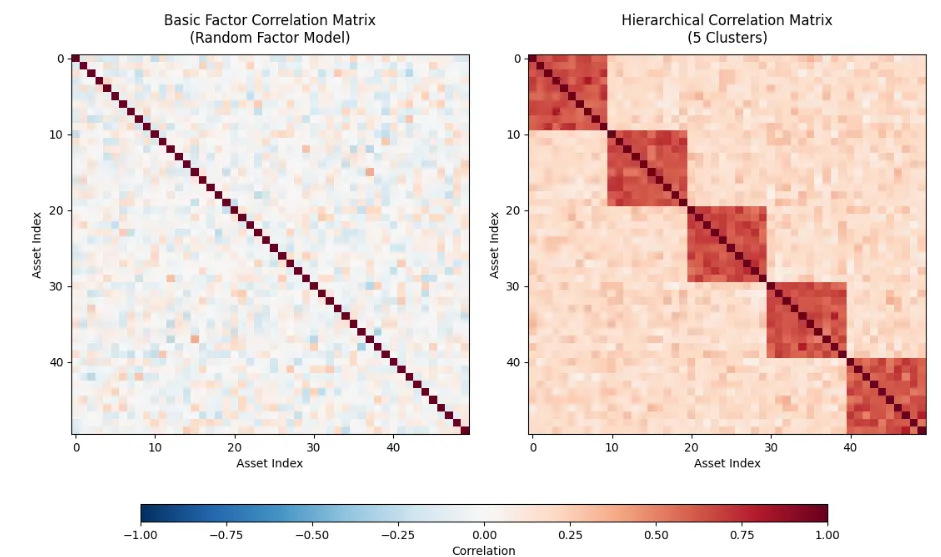
这种方法使我们能够评估横截面系统性策略在不同相关性条件下的表现。例如,在“危机时期”,资产之间的相关性往往会趋近于 1。这对投资组合构成重大风险,因为它会严重削弱分散化效果。因此,了解策略在这些时期的表现,对于全面把握策略或投资组合的风险特征非常有帮助。
我们合成时间序列生成器中要开发的第一个组件,就是用于生成相关矩阵的类层次结构。该结构后续将被用于在各种时间序列模型下(其中一些模型我们已在《使用 Python 模拟布朗运动》和《使用 Python 模拟几何布朗运动》中讨论过)生成具有相关性的价格路径。
我们将采用抽象基类(Abstract Base Class, ABC)的概念,定义一个所有派生类都必须遵循的统一接口。这样可以确保我们在不改变合成数据生成器其他模块的前提下,“即插即用”地替换不同的相关矩阵生成器类。这一设计模式已在我们的开源回测软件 QSTrader 中被广泛采用,如果您之前使用过该工具,可能已熟悉这种做法。
我们将在本工具的其他组件(如时间序列模型和相关路径生成器)中同样采用这种面向对象的设计方法。尽管乍看之下这似乎给软件引入了不必要的复杂性,但我们将在后续文章中通过示例展示其价值——它能让我们轻松扩展至其他相关矩阵生成模型和时间序列生成模型。
抽象基类
定义类层次结构的第一步是导入所需的库。我们在 correlation.py 文件开头导入 Python 的 ABC 工具,以及第三方库 NumPy 和 SciPy。特别地,我们需要从 SciPy 的统计模块中导入 random_correlation 方法:
# correlation.pyfrom abc import ABC, abstractmethodimport numpy as npfrom scipy.stats import random_correlation
correlation.py 文件,定义 CorrelationMatrixGenerator 的抽象基类(ABC)接口。该接口包含一个初始化方法(__init__),接收一个参数 n,表示矩阵的维度。由于相关矩阵是 n×n 的方阵,因此只需传入一个整数即可。此外,我们还加入了 **kwargs 语法,以便在更复杂的矩阵生成方法中传入模型特定的关键字参数。该方法仅创建两个类实例属性 n 和 kwargs:# ..# correlation.py# ..class CorrelationMatrixGenerator(ABC):"""Abstract base class for correlation matrix generators."""def __init__(self, n: int, **kwargs):"""Initialize the correlation matrix generator.Args:n: Size of the correlation matrix (n x n)**kwargs: Additional keyword arguments for specific implementations"""self.n = nself.kwargs = kwargs
generate。通过使用 @abstractmethod 装饰器,我们告知 Python:任何继承该抽象基类的子类都必须实现此方法,因为此处未提供默认实现。可以看出,该方法设计为返回一个 NumPy 的 ndarray 对象,其中包含相关矩阵的实际浮点数值:# ..# correlation.py# ..@abstractmethoddef generate(self) -> np.ndarray:"""Generate an n x n correlation matrix."""pass
继续编写 correlation.py,我们现在提供一个名为 _make_positive_semidefinite 的方法,其目的是确保我们生成的任何随机相关矩阵都满足半正定性(positive semidefiniteness)这一数学性质。为了便于理解后续代码,有必要对此稍作解释。如果您之前学过线性代数,可以跳过本段说明;否则,请继续阅读!
半正定性意味着:当我们使用相关矩阵生成器类来生成相关随机数据时,结果将是合理且有意义的,不会导致诸如“负方差”等不可能出现的情形。若缺乏这一性质,在生成相关时间序列时可能会失败,或产生无意义的结果。
该方法采用特征值分解(eigenvalue decomposition)——一种线性代数技术,将矩阵分解为其基本组成部分。这大致类似于将一个和弦分解为单个音符。每一个对称矩阵(包括相关矩阵)都可以表示为三个矩阵的乘积:特征向量矩阵(代表相关性的“方向”)、特征值对角矩阵(代表每个方向上的“强度”),以及特征向量矩阵的转置。
当一个相关矩阵不是半正定时,它会包含负的特征值,这是有问题的。以下算法通过将所有负特征值设为一个极小的正数(例如 ϵ=10−8)来修正这一问题。这样做能有效剔除“不可能”的相关结构,同时尽可能保留原始矩阵的整体结构。在利用修正后的特征值和特征向量重构矩阵后,还需对其进行归一化处理,以确保结果仍是一个有效的相关矩阵:即所有对角线元素严格等于 1.0(因为任一时间序列与自身完全相关),并保证矩阵对称(因为资产 A 与 B 的相关性必须等于 B 与 A 的相关性)。
这种方法在通过各种算法或用户输入生成相关矩阵时尤为有用,因为数值误差或相互冲突的设定可能导致数学上无效的矩阵。通过应用此修正,以下代码可确保后续操作(包括用于生成实际相关时间序列的 Cholesky 分解,这将在后续文章中使用)能够可靠运行,避免因数学不一致性而导致程序崩溃或输出无意义结果。
具体实现上,该方法首先使用 NumPy 的 linalg.eigh 方法获取特征值和特征向量。然后将所有负特征值替换为一个接近零的小正数 ϵ。接着,通过矩阵乘法重构新矩阵:
Rnew=V⋅diag(λcorrected)⋅V⊤
其中 V 是特征向量矩阵,λcorrected 是修正后的特征值。随后对矩阵进行归一化,使其成为有效的相关矩阵。最后,将对角线元素强制设为 1,并确保矩阵对称:
# ..# correlation.py# ..def _make_positive_semidefinite(self, matrix: np.ndarray) -> np.ndarray:"""Ensure matrix is positive semidefinite and valid correlation matrix."""# Eigenvalue decomposition with proper scalingeigenvalues, eigenvectors = np.linalg.eigh(matrix)# Set negative eigenvalues to small positive valueeigenvalues[eigenvalues < 0] = 1e-8# Reconstruct matrixmatrix = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T# Normalize to ensure it's a correlation matrix# Extract diagonal elementsd = np.sqrt(np.diag(matrix))# Avoid division by zerod[d == 0] = 1# Normalizematrix = matrix / np.outer(d, d)# Ensure diagonal is exactly 1 and matrix is symmetricnp.fill_diagonal(matrix, 1.0)matrix = (matrix + matrix.T) / 2return matrix
至此,我们完成了基类 CorrelationMatrixGenerator 的实现。该类本身并不能生成任何相关矩阵,而是需要通过实现其派生子类,利用不同模型来生成相关矩阵——这些模型在真实感上各有差异,可与基于实证数据得到的相关矩阵进行比较。
基础因子相关矩阵生成器(Basic Factor Correlation Matrix Generator)
我们将要实现的第一个相关矩阵生成器名为 BasicFactorCorrelationGenerator。首先,我们在下方的信息框中详细说明其背后的理论依据,然后讨论具体的代码实现。
下面的 generate 方法使用一种基于因子模型(factor models)的巧妙技术来生成随机相关矩阵。因子模型在金融领域被广泛用于解释:少量潜在的共同因子如何驱动大量资产之间的相关性。如果我们假设时间序列受若干隐藏的共同因子影响,同时叠加各自独立的特异性扰动,那么由此自然产生的相关结构将自动满足数学上的有效性。这种方法巧妙地避开了逐元素直接构造相关矩阵的难题——后者常常导致数学不一致(如非半正定)的问题。
具体实现上,该方法首先创建一个维度为 n×k 的随机“因子载荷”矩阵 W,其中 n 是我们希望关联的变量数量,k(即随机因子参数)是隐藏因子的数量,通常远小于 n。每一行表示某个变量对各个隐藏因子的敏感程度。当我们计算 W@W⊤ 时,会得到一个 n×n 的矩阵,它捕捉了变量因共享共同因子而产生的相关性。这种构造方式天然保证了半正定性,因为任何形如 WW⊤ 的矩阵在数学上都是半正定的——这是线性代数中的一个基本结论。随后,方法还会加上一个极小的对角项(例如 10−8⋅I),以提升数值稳定性,避免后续计算中因接近零的值而引发问题。
最后几步将这个类似协方差的矩阵转换为标准的相关矩阵。通过将每个元素除以其对应标准差(即对角线元素的平方根)的乘积,我们将数值归一化到相关系数应有的区间 [−1,1] 内。接着,方法确保对角线元素严格等于 1.0,并通过对矩阵与其转置取平均来强制其完全对称——以此消除浮点运算可能带来的微小数值偏差。最后,np.clip 操作作为一道安全网,将因数值精度限制而略微超出 [−1,1] 范围的值裁剪回有效区间。这一方法在生成具有真实感的相关结构的同时,无需依赖基类中所需的修正流程,即可保证数学上的有效性。
在该类的初始化方法 __init__ 中,我们可以看到新增了一个整型关键字参数(kwarg),用于指定影响相关矩阵的随机因子数量:
# ..# correlation.py# ..class BasicFactorCorrelationGenerator(CorrelationMatrixGenerator):"""Basic factor-based correlation matrix generator that createsrandom valid correlation matrices. Uses a method that guaranteespositive semi-definiteness."""def __init__(self, n: int, random_factor: int = None, **kwargs):"""Initialize the basic factor correlation generator.Args:n: Size of the correlation matrixrandom_factor: Factor for random matrix generation"""super().__init__(n, **kwargs)self.random_factor = random_factor or max(n + 50, 2 * n)
以下代码在 generate 方法中首次实现了基类中定义的抽象方法。首先创建一个矩阵 W,其初始值为服从高斯(正态)分布的随机数,形状为 n×k。接着通过矩阵乘法 W@W⊤ 构造出一个协方差矩阵 C。然后,将一个很小的数值 ϵ 乘以同维度的单位矩阵,并加到 C 上,从而将其所有对角线元素略微增大,以提升数值稳定性。
随后,计算 C 对角线元素的平方根(即各变量的标准差),并利用这些标准差对 C 进行归一化,从而得到一个有效的相关矩阵。接着,将该矩阵的对角线元素强制设为 1,并确保矩阵对称。最后,将任何超出 [−1,1] 区间的数值裁剪(clip)至 -1 或 1:
# ..# correlation.py# ..def generate(self) -> np.ndarray:"""Generate a random valid correlation matrix."""# Generate random factor loadings and create correlation from them# This guarantees a valid correlation matrix# Generate random factor loadings matrix# More rows than columns ensures positive definitenessW = np.random.randn(self.n, self.random_factor)# Create covariance matrixS = W @ W.T# Add small diagonal term for numerical stabilityS += np.eye(self.n) * 1e-6# Convert to correlation matrix# Extract standard deviationsstd_devs = np.sqrt(np.diag(S))# Normalize to get correlation matrixcorr_matrix = S / np.outer(std_devs, std_devs)# Ensure exact propertiesnp.fill_diagonal(corr_matrix, 1.0)corr_matrix = (corr_matrix + corr_matrix.T) / 2 # Ensure perfect symmetry# Clip any numerical errorscorr_matrix = np.clip(corr_matrix, -1, 1)return corr_matrix
至此,我们完成了 BasicFactorCorrelationMatrixGenerator 类的实现。尽管该模型可用于生成基本的相关矩阵,进而构造合成的相关时间序列,但它与基于真实股票数据的经验相关矩阵相比,仍远不够逼真。
为了提升模型的真实感,并进一步展示“即插即用”式替换相关矩阵生成器类的能力,我们将开发另一种相关矩阵生成模型——基于股票板块/行业聚类结构的层次化相关矩阵生成器(Hierarchical Correlation Matrix Generator)。
层次化相关矩阵生成器(Hierarchical Correlation Matrix Generator)
以下代码片段实现了 HierarchicalCorrelationMatrixGenerator 类。其初始化方法 __init__ 需要多个关键字参数(kwargs)来配置模型参数。具体包括:
板块聚类的数量(整数); 板块内部(intra-cluster)和板块之间(inter-cluster)的相关系数范围; 一个噪声参数,用于在相关系数中引入随机扰动。
这些参数均可在后续文章中定义的配置文件中进行调整,使您能够灵活设定模拟股票资产价格中包含多少个板块,以及各板块内部及板块之间的价格联动程度(即相关性强弱)。
# ..# correlation.py# ..class HierarchicalCorrelationMatrixGenerator(CorrelationMatrixGenerator):"""Generates correlation matrices with hierarchical clustering structure.This creates blocks of higher correlations to simulate sector/industry clustering."""def __init__(self,n: int,n_clusters: int = None,intra_cluster_corr: float = 0.7,inter_cluster_corr: float = 0.2,noise_level: float = 0.1,**kwargs):"""Initialize the hierarchical correlation generator.Args:n: Size of the correlation matrixn_clusters: Number of clusters (default: sqrt(n))intra_cluster_corr: Base correlation within clustersinter_cluster_corr: Base correlation between clustersnoise_level: Amount of random noise to add"""super().__init__(n, **kwargs)self.n_clusters = n_clusters or int(np.sqrt(n))self.intra_cluster_corr = intra_cluster_corrself.inter_cluster_corr = inter_cluster_corrself.noise_level = noise_level
与 BasicFactorCorrelationMatrixGenerator 类似,我们也需要为 HierarchicalCorrelationMatrixGenerator 子类实现 generate 方法。我们首先在下方的信息框中详细说明所采用的方法思路,然后逐段解析代码实现。
HierarchicalCorrelationMatrixGenerator 生成的相关矩阵旨在模拟金融市场中常见的层次化结构:同一板块内的资产(例如科技股)彼此之间的联动性明显强于不同板块的资产。
这种模式反映了现实世界中的经济关系——同一行业的公司面临相似的市场环境、监管变化和消费者趋势,因此其价格走势在板块内部高度相关,而板块之间则相关性较弱。该生成器通过将资产划分为若干聚类(即板块),并根据资产对是否属于同一聚类来分配不同的相关系数,从而捕捉这一现象。
具体实现上,算法首先创建一个基础矩阵,所有元素初始化为板块间相关系数(通常较低,例如 0.2),代表不同板块资产之间的基准关联水平。接着,将 n 个资产大致均等地划分为指定数量的聚类,并将无法整除的余数资产均匀分配到各聚类中。
对于每个聚类,算法将其对应的矩阵对角块(diagonal block)覆盖为更高的板块内相关系数(通常约为 0.7),从而在矩阵对角线上形成明显的“高相关区块”。这种结构直接模仿了真实市场数据的相关矩阵——当资产按板块排序时,对角线上会出现明亮的方块(表示同类资产高度相关),而远离对角线的区域则较暗淡(表示跨板块相关性较弱)。
为避免结构过于刻板、显得不自然,方法会向矩阵中加入从正态分布抽取的随机噪声,使相关模式更具真实感和多样性。为保持矩阵必须满足的对称性,噪声矩阵会与其转置取平均进行对称化处理(这一点与之前的基础相关矩阵生成器一致)。
随后,将所有元素裁剪至有效相关系数范围 [−1,1] 内,并将对角线精确设为 1.0。最后,generate 方法调用基类中继承的 _make_positive_semidefinite 函数,确保矩阵在数学上是半正定的,从而保证其作为有效相关矩阵的合法性。
代码实现细节如下:
generate 方法的第一部分创建一个 n×n 的矩阵,所有元素初始值均为板块间相关系数。接下来,计算每个聚类的大小,生成一个聚类尺寸数组。随后,对每个聚类,利用 NumPy 的切片语法(slicing notation),将矩阵中对应子块的元素设置为板块内相关系数。这是通过迭代更新 start_idx 和 end_idx(每次增加当前聚类的大小)来精确定位每个对角子块的位置实现的。
至此,整个矩阵的元素要么是板块间相关系数,要么在对角线上的某些区块内是板块内相关系数。为了增强真实感,需为这些相关系数引入一定变异。为此,向矩阵中每个元素添加服从高斯分布的噪声,其标准差由 noise_level 参数控制。该噪声矩阵同样被强制对称化后,再加到原始相关矩阵上。
最后,如同前一个相关矩阵生成器一样,将所有对角线元素设为 1,并确保整个矩阵为半正定。
# ..# correlation.py# ..def generate(self) -> np.ndarray:"""Generate a hierarchical correlation matrix."""# Initialize with inter-cluster correlationmatrix = np.full((self.n, self.n), self.inter_cluster_corr)# Assign assets to clusterscluster_sizes = [self.n // self.n_clusters] * self.n_clusters# Distribute remaining assetsfor i in range(self.n % self.n_clusters):cluster_sizes[i] += 1# Create intra-cluster correlationsstart_idx = 0for cluster_size in cluster_sizes:end_idx = start_idx + cluster_sizematrix[start_idx:end_idx, start_idx:end_idx] = self.intra_cluster_corrstart_idx = end_idx# Add noisenoise = np.random.normal(0, self.noise_level, size=(self.n, self.n))noise = (noise + noise.T) / 2 # Make symmetricmatrix += noise# Ensure correlations are in [-1, 1]matrix = np.clip(matrix, -1, 1)# Set diagonal to 1np.fill_diagonal(matrix, 1.0)# Make positive semidefinitematrix = self._make_positive_semidefinite(matrix)return matrix
至此,correlation.py 文件已完成。该模块没有入口点(entrypoint),其唯一目的就是实现上述相关矩阵生成器类。为了直观地观察这些类所生成实例的实际效果,我们将在下一节编写一个小型可视化脚本,将两类生成器产生的代表性相关矩阵并排绘制出来。
矩阵可视化
为了可视化这两种相关矩阵生成器的结果,我们可以使用 Python 的 NumPy 和 Matplotlib 库。特别是,可以利用 Matplotlib 中的 imshow 方法,将二维 NumPy 矩阵输出绘制成热力图(heatmap),并配以合适的颜色映射(colormap)。
由于相关矩阵中的元素取值范围为 [−1,1],使用发散型(diverging)颜色映射(例如 RdBu_r,即红-蓝反转色谱)比使用感知均匀的色谱(如默认的 viridis)更为合适。这种色谱能更清晰地区分极端负相关和正相关:深红色区域代表强负相关,深蓝色区域代表强正相关。
我们将创建一个名为 visualization.py 的独立脚本,并将其与 correlation.py 放在同一目录下。这个简短的脚本将演示如何从每个相关矩阵生成器中采样并绘图,从而直观展示它们所能生成的矩阵类型。
第一步是导入 NumPy 和 Matplotlib 库,以及从 correlation.py 中导入两个生成器类:
# visualization.pyimport matplotlib.pyplot as pltimport numpy as npfrom correlation import (BasicFactorCorrelationMatrixGenerator,HierarchicalCorrelationMatrixGenerator)
接着,我们为 NumPy 的伪随机数生成器(PRNG)设置一个随机种子,以确保您所看到的矩阵样本与下图中展示的结果完全一致。我们将相关矩阵的维度设为 200×200,并将层次化矩阵生成器配置为使用 5 个聚类。
随后,我们分别实例化这两个相关矩阵生成器,并调用各自的 generate 方法,从每个类实例中获取一个样本矩阵:
# ..# visualization.py# ..# Set random seed for reproducibilitynp.random.seed(42)# Parametersn = 50 # Size of correlation matricesn_clusters = 5 # Number of clusters for hierarchical generator# Generate correlation matricesbasic_generator = BasicFactorCorrelationMatrixGenerator(n=n)basic_matrix = basic_generator.generate()hierarchical_generator = HierarchicalCorrelationMatrixGenerator(n=n,n_clusters=n_clusters,intra_cluster_corr=0.7,inter_cluster_corr=0.2,noise_level=0.1)hierarchical_matrix = hierarchical_generator.generate()
脚本的其余部分主要用于设置 Matplotlib 的各项参数,以创建子图,并添加标题、坐标轴标签以及颜色条。我们首先创建一个图形(figure)实例,然后生成两个独立的坐标轴(axis)对象。接着,使用 Matplotlib 的 imshow 方法在每个坐标轴上分别绘制一个热力图,数值范围为 [−1,1],并采用前述的红-蓝反转发散型色谱(RdBu_r)。
每个坐标轴都设置了特定的子标题、x 轴和 y 轴标签,并关闭了默认网格线。我们还调整了子图之间的间距,以确保图像清晰可读。最后,添加一个颜色条,用以说明颜色的深浅或色调如何对应矩阵中的相关系数值。
默认情况下,该脚本会直接在一个独立窗口中显示图像(如果在 Jupyter Notebook 中运行,则会显示在输出单元格中)。如果您希望将图像保存为 PNG 文件,只需取消注释最后一行代码,相关矩阵图便会保存到磁盘中:
# ..# visualization.py# ..# Create visualization with adjusted spacingfig = plt.figure(figsize=(14, 7))# Create subplot with more space at bottom for colorbarax1 = plt.subplot(1, 2, 1)ax2 = plt.subplot(1, 2, 2)# Plot basic factor correlation matrixim1 = ax1.imshow(basic_matrix, cmap='RdBu_r', vmin=-1, vmax=1, aspect='auto')ax1.set_title('Basic Factor Correlation Matrix\n(Random Factor Model)', fontsize=12, pad=10)ax1.set_xlabel('Asset Index')ax1.set_ylabel('Asset Index')ax1.grid(False)# Plot hierarchical correlation matrixim2 = ax2.imshow(hierarchical_matrix, cmap='RdBu_r', vmin=-1, vmax=1, aspect='auto')ax2.set_title(f'Hierarchical Correlation Matrix\n({n_clusters} Clusters)', fontsize=12, pad=10)ax2.set_xlabel('Asset Index')ax2.set_ylabel('Asset Index')ax2.grid(False)# Adjust subplot positioning to make room for title and colorbarplt.subplots_adjust(bottom=0.25, top=0.9, left=0.08, right=0.95, wspace=0.15)# Add a shared colorbar with better positioningcbar_ax = fig.add_axes([0.15, 0.1, 0.7, 0.03]) # [left, bottom, width, height]fig.colorbar(im2, cax=cbar_ax, label='Correlation', orientation='horizontal')# Display the plotplt.show()# Optional: Save the figure# plt.savefig('correlation_matrices_comparison.png', dpi=150, bbox_inches='tight')
在合适的虚拟环境中,您可以在终端中运行以下命令:
$ python3 visualization.py该脚本的运行结果如下图所示。左侧展示的是由基础因子相关矩阵生成器(Basic Factor Correlation Matrix Generator)生成的示例矩阵,右侧则展示了由层次化相关矩阵生成器(Hierarchical Correlation Matrix Generator)生成的示例矩阵。可以看出,左侧矩阵的非对角线元素为小幅随机值,而右侧矩阵则呈现出明显的块状结构,反映了板块内部的相关性。
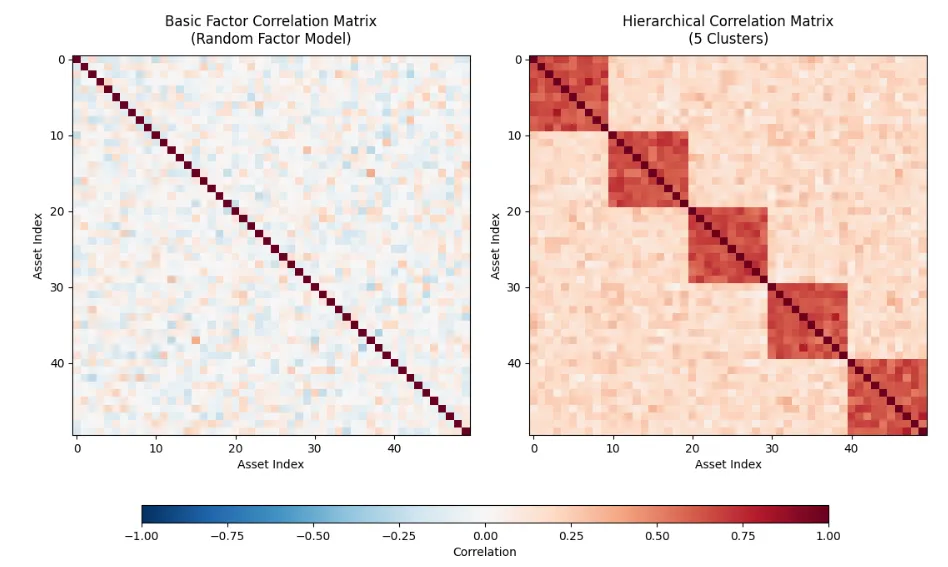
Next Steps:
在接下来的文章中,这些生成器将被用于提供生成相关时间序列所需的相关结构,进而构成一个股票合成数据生成器的基础。
所生成的数据集将用于机器学习模型的“预训练”(pre-training):我们首先在合成数据上训练机器学习模型以学习其统计特性,然后再在真实金融数据上对模型进行“微调”(fine-tuning)。
在此之前由于获得部分粉丝反应需要基础的书籍介绍,我也会提供一些其他方向的文章。
