GESP2025年12月六级编程题1解析
- 2026-01-17 13:02:56
GESP2025年12月六级编程题1比较有难度, 超出了考纲范围.题目如下:
给定一棵有 n 结点的有根树 T,结点依次以 1,2,...,n 编号,根结点编号为 1。方便起见,编号为 i 的结点称为结点 i。
初始时 T 中的结点均为白色。你需要将T 中的若干个结点染为黑色,使得所有叶子到根的路径上至少有一个黑色结点。
将结点 i 染为黑色需要代价 c_i,你需要在满足以上条件的情况下,最小化染色代价之和。
叶子是指 T 中没有子结点的结点。
## 输入格式
第一行,一个正整数 n,表示结点数量。
第二行,n-1 个正整数f_2,f_3,...,f_n,其中 f_i 表示结点 i 的父结点的编号,保证 f_i<i。
第三行,n 个正整数c_1,c_2,...,c_n,其中 c_i 表示将结点 i 染为黑色所需的代价。
## 输出格式
一行,一个整数,表示在满足所有叶子到根的路径上至少有一个黑色结点的前提下,染色代价之和的最小值。
## 输入输出样例 #1
### 输入 #1
4
1 2 3
5 6 2 3
### 输出 #1
2
## 输入输出样例 #2
### 输入 #2
7
1 1 2 2 3 3
64 16 15 4 3 2 1
### 输出 #2
10
## 说明/提示
对于 40% 的测试点,保证2<= n<= 16。
对于另外 20% 的测试点,保证f_i=i-1。
对于所有测试点,保证 2<= n<= 10^5,1<= c_i<= 10^9。
看一下数据规模,40%的测试点,保证 n<= 16 , 学生们都可以想到暴力, 但具体怎么学暴力,很多学生写不出来.
另外 20% 的测试点,保证f_i=i-1 , 这个特殊条件,可以模拟一下,就是一条链,见下图:

链的分近乎白送, 因为1是根节点,链只有一个叶子节点, 那么这条链上谁被染成黑色都行,那就打擂台找个最小值就可以了,核心代码如下:
cin>>n; ll ba,minn=LONG_LONG_MAX; bool cs2=true; //一条链的情况 for(int i=2;i<=n;i++){ cin>>ba; e[ba].push_back(i); if(ba!=i-1) cs2=false; //判断是否为链 fa[i]=ba; havson[ba]=true; } for(int i=1;i<=n;i++){ cin>>c[i]; minn=min(minn,c[i]); //整颗树的最小值 if(!havson[i]) leaf.push_back(i); //叶子节点 } if(cs2){ //20分 链的情况 cout<<minn; return 0; } |
轻松20分得到
再说暴力枚举,怎么枚举? n<=16,每个点可以染色也可以不染色,一共2^16= 65536个状态,我们可以枚举每个状态,判断所有的叶子节点到根节点的路径上是否都有染色节点, 如果都有,就是一种有效状态, 在所有有效状态中,求染色费用的最小值. 代码如下: 融合了链的情况,可以得60分.这个确实需要很强的基本功.
#include <bits/stdc++.h> //万能头文件 using namespace std; //使用标准的命名空间 using ll =long long; const int N=1e5+10; ll n,c[N],fa[N];//fa[i]表示以i的爸爸 vector<ll> e[N]; vector<ll> leaf; //叶子节点的集合 bool havson[N]; bool isok(int a){ int col[30]={}; for(int i=1;i<=n;i++){ if(a&(1<<(i-1))) col[i]=1; } for(ll s:leaf){ //判断是否所有儿子都至少有1个染色的爸爸 bool flag=0; ll k=s; while(k!=0){ if(col[k]) { flag=1; break; } k=fa[k]; } if(!flag) return 0; } return 1; } int main(){ //主函数win+D cin>>n; ll ba,minn=LONG_LONG_MAX; bool cs2=true; //一条链的情况 for(int i=2;i<=n;i++){ cin>>ba; e[ba].push_back(i); if(ba!=i-1) cs2=false; //判断是否为链 fa[i]=ba; havson[ba]=true; } for(int i=1;i<=n;i++){ cin>>c[i]; minn=min(minn,c[i]); //整颗树的最小值 if(!havson[i]) leaf.push_back(i); //叶子节点 } if(cs2){ //20分 链的情况 cout<<minn; return 0; } if(n<20){ //暴力 int N=1<<n; ll min20=LONG_LONG_MAX; for(int a=1;a<N;a++){ //枚举所有状态,0不用枚举 ll sum=0; if(isok(a)){//判断所有的叶子节点到根节点的路径上是否都有染色节点 for(int i=1;i<=n;i++){//累加染色节点 if(a&(1<<(i-1))) sum+=c[i]; } } if(sum!=0){ //是有效状态 min20=min(min20,sum); } } cout<<min20; } return 0; //函数结束 } |
再说100分的解法, 其实就是一个树上的DP,但树上的DP,六级考纲中根本就没提,这是CSP提高组的内容. 六级动态规划(DP)部分,只提到一维动态规划和简单的背包问题, 这个也没地说理去, 所以只能超前学一些.
GESP六级考纲如下:
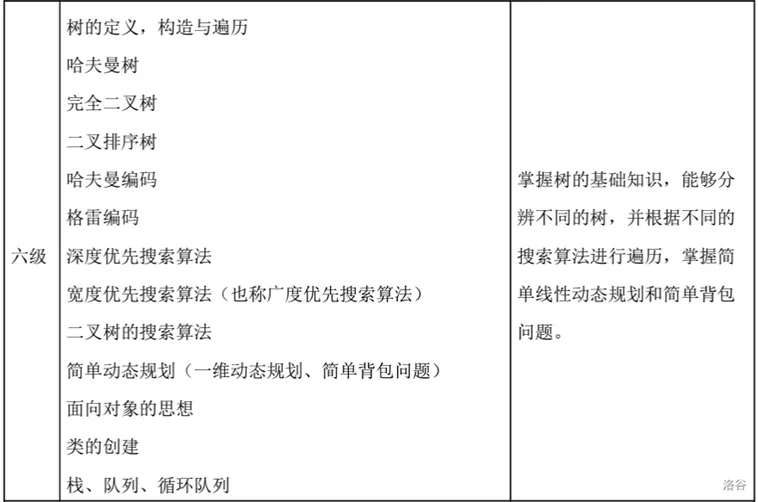
这题要用树上的DP思想去考虑就简单了.
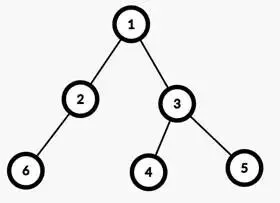
f[i]表示以i为根的子树的染色代价之和最小值,则第一种情况i节点染色,子树就不需要染色了,f[i]=c[i];
第二种情况: i节点不染色,需要i的子树自己染色, 则f[i]=sum(f[son]),即所有子树的最小染色代价之和;
两种情况取最小值即可.
核心代码如下:
ll n,c[N],f[N]; vector<ll> e[N]; ll dfs(ll k){ if(f[k]>0) return f[k]; f[k]=c[k]; ll sum=0; for(int son:e[k]){ sum+=dfs(son); } if(sum==0) return f[k]; else return min(f[k],sum); } int main(){ //主函数win+D cin>>n; ll fa; for(int i=2;i<=n;i++){ cin>>fa; e[fa].push_back(i); } for(int i=1;i<=n;i++) cin>>c[i]; cout<<dfs(1); return 0; //函数结束 } |
