Python版 | 如何用一张图看透多变量间的“爱恨情仇”?
- 2026-01-27 22:46:55
未经允许,不可抄袭,转载请注明出处!
在处理多维度数据时,我们常面临一个难题:当变量变多了,如何快速理清它们之间的复杂联系?此时,一张具有“高级感”的多变量成对关系矩阵图(Pairwise Correlation Matrix)便是破局的关键。
这种图表的核心逻辑在于“降维打击”:它将 张零散的散点图,巧妙地压缩进一个结构化矩阵中。它常作为 Nature/Cell 等顶级期刊的常客,用于展示不同实验条件(如不同凝聚剂、药物或蛋白处理)下的整体关联性。
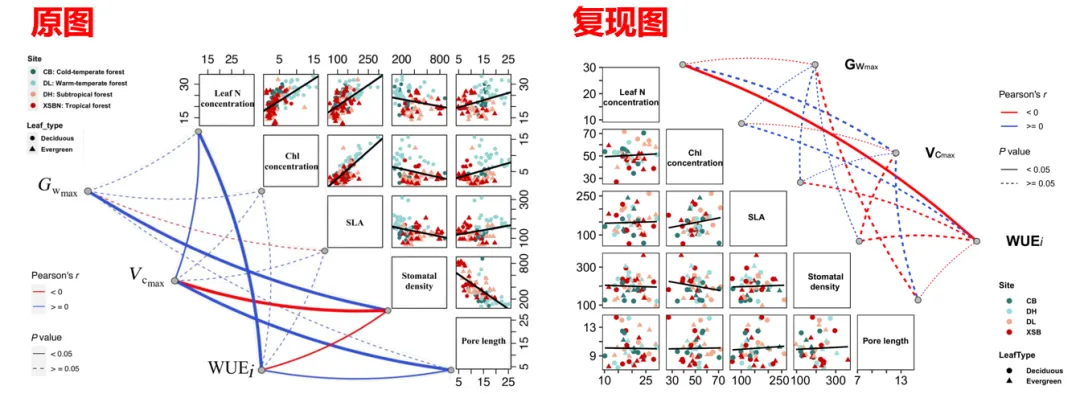
今天将复现 Nature 文章中 (Park, S., Merino-Urteaga, R., Karwacki-Neisius, V. et al. Native nucleosomes intrinsically encode genome organization principles. Nature 643, 572–581 (2025). https://doi.org/10.1038/s41586-025-08971-7) 的 Fig. 3a
原图
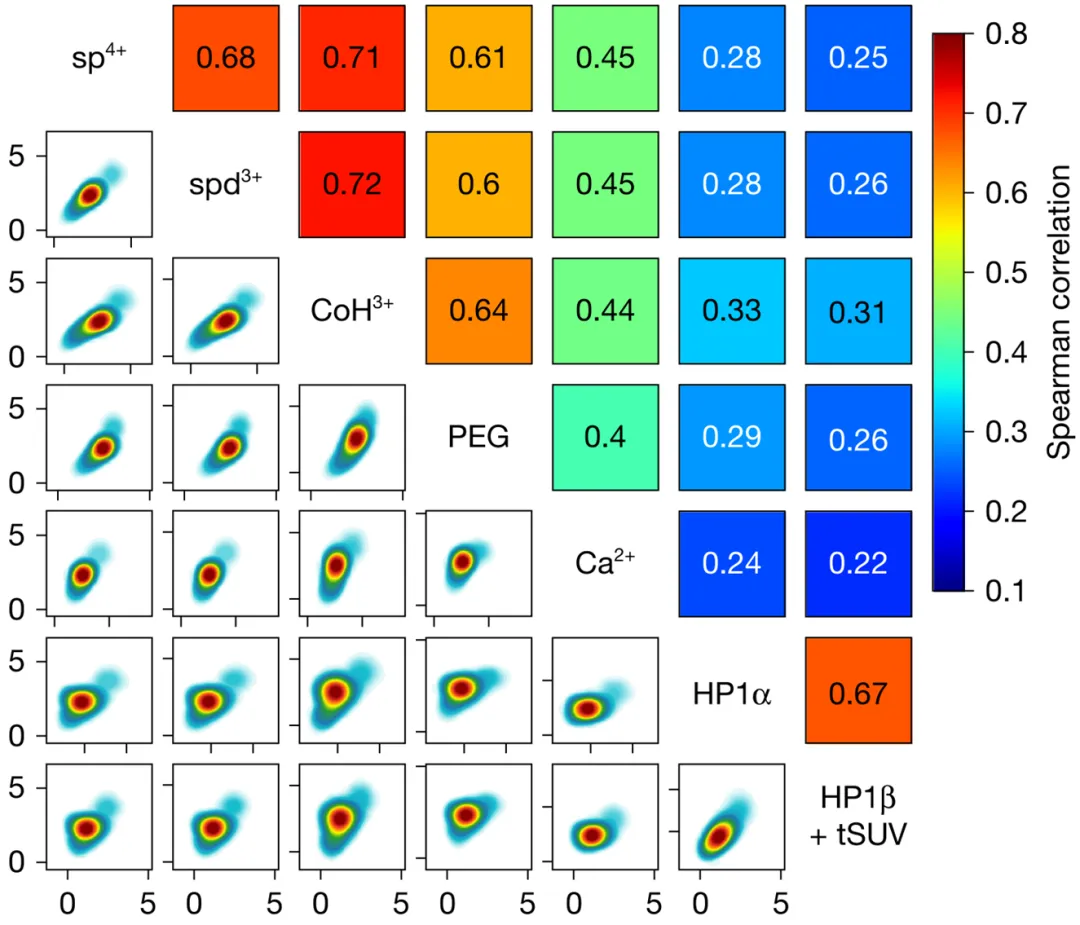
这张图的设计是:
上三角:相关性(Correlation)
每一个方块:两个 condensing agent 的相关性 数字与颜色:展示的是 Spearman 或 Pearson 相关系数。颜色越深、数值越大,说明这两种凝聚剂对不同 DNA 序列的作用越“步调一致”。
👉 回答的问题是:
用 A 和用 B,得到的 condensability score 排名是不是一致?或者说,如果凝聚剂 A 认为序列 1 比序列 2 更容易发生凝聚,凝聚剂 B 是否也持有同样的观点?如果相关性极高,说明这两种剂量的作用遵循某种普适的规律。
下三角:二维核密度(2D density)
每个点:一个基因 / 序列 / 测量对象 云图:点在二维空间中的密度分布 看趋势 + 看离散度
👉 比单纯散点图更稳健,尤其在样本量巨大时,能有效避免数据堆叠,让你一眼看清大部队的“阵型”。
对角线:变量名(而不是分布)
不强调单变量分布 把视觉注意力全部集中在“变量之间的关系”
当你有一堆变量,想同时看它们“两两之间是什么关系”时,就用这类图。
复现图
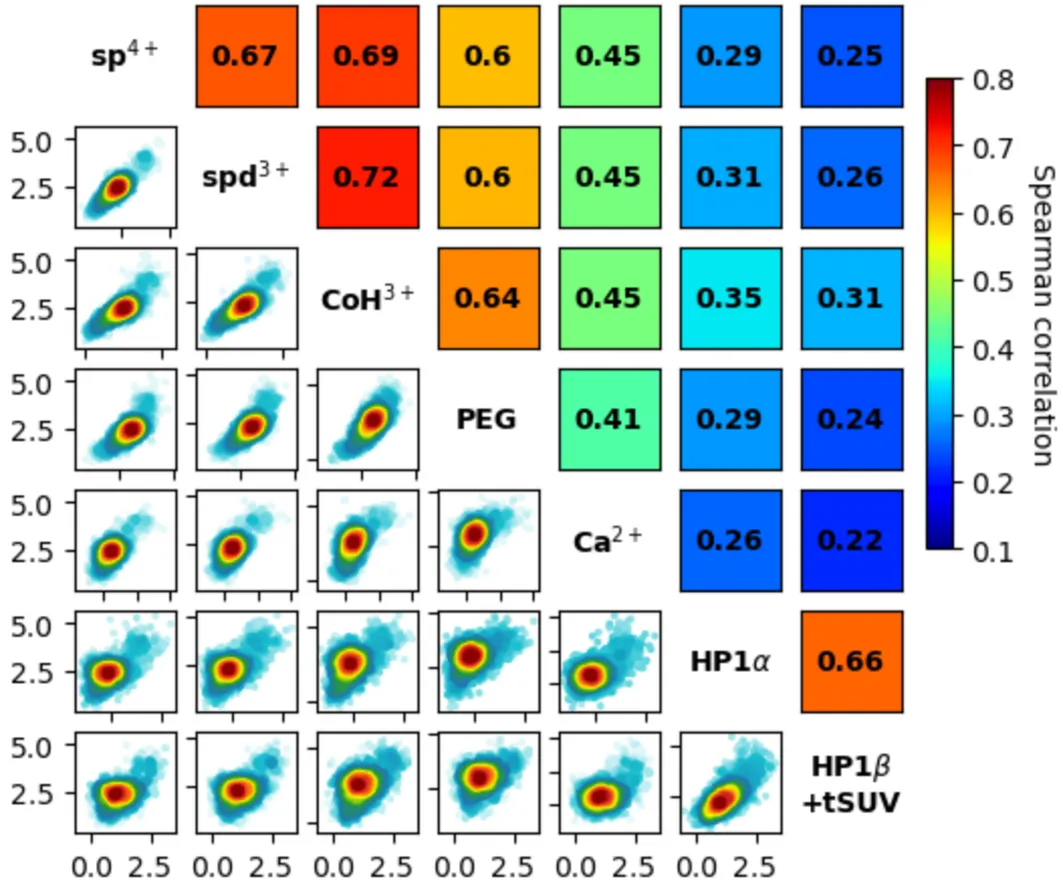
本次使用 Python 语言完成绘图!
加载库,读入数据
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport matplotlib.gridspec as gridspecfrom matplotlib.colors import LinearSegmentedColormapfrom scipy import statsfrom scipy.interpolate import interpn# 读取数据df = pd.read_csv("dkey_data_sampled.csv")
此数据为模拟数据,无实际意义,如需文末可以自助获取。
定义绘图函数
# 绘制密度散点图def density_scatter (X,Y,xlim=[None,None],ylim=[None,None],bins=20,density=False,sort=True,cbar=True,cmap=None,s=3,xlabel=None,ylabel=None,title=None,fig_width=4,fig_height=3,ax=None,save=False,save_path='./',show=True,note='',**kwargs):# 如果没有传入坐标轴对象,则创建新的图形和坐标轴if ax == None:fig, ax = plt.subplots(nrows=1,ncols=1,figsize=(fig_width, fig_height))make_fig = True # 标记为新创建的图形else:make_fig = False # 标记为使用传入的坐标轴# 过滤数据:去除NaN值和超出限制范围的数据点newX, newY = [], []for x, y in zip(X, Y):if np.isnan(x) or np.isnan(y): # 跳过包含NaN的数据点continueif xlim[0] != None and x < xlim[0]: # 跳过小于x下限的数据continueif xlim[1] != None and x > xlim[1]: # 跳过大于x上限的数据continueif ylim[0] != None and y < ylim[0]: # 跳过小于y下限的数据continueif ylim[1] != None and y > ylim[1]: # 跳过大于y上限的数据continuenewX.append(x) # 添加有效x值newY.append(y) # 添加有效y值# 更新数据为过滤后的结果X, Y = newX, newYdel newX # 删除临时变量释放内存del newY # 删除临时变量释放内存# 如果没有指定颜色映射,则创建自定义的颜色映射if cmap == None:# "jet-like" colormap with white backgroundpastel_jet = LinearSegmentedColormap.from_list('white_viridis',[(0, '#ffffff'),(0.03, 'tab:cyan'),(0.1, 'tab:blue'),(0.3, 'tab:green'),(0.5, 'yellow'),(0.7, 'tab:orange'),(0.9, 'tab:red'),(1, 'darkred')],N=256)cmap = pastel_jet # 使用自定义颜色映射# 创建2D直方图来计算数据点的密度分布data, X_e, Y_e = np.histogram2d(X,Y,bins = bins, # 直方图的分箱数量density=density) # 是否归一化为概率密度# interpolate the 2d histogram to a continuous density function# 对2D直方图进行插值,得到连续的密度函数Z = interpn((0.5*(X_e[1:]+X_e[:-1]), # x方向的网格中心点0.5*(Y_e[1:]+Y_e[:-1])), # y方向的网格中心点data, # 直方图数据np.vstack([X, Y]).T, # 数据点的坐标,转置为(n,2)形状method = "splinef2d", # 使用样条插值方法bounds_error = False) # 边界外的点返回NaN而不报错# convert nan to zero# 将插值结果中的NaN值转换为0.0Z[np.where(np.isnan(Z))] = 0.0# sort the points by density, so that the densest points are plotted last# 按密度值排序,使得密度最低的点先绘制,密度最高的点最后绘制(避免遮挡)if sort :idx = Z.argsort() # 获取按密度升序排列的索引X, Y, Z = np.asarray(X)[idx], np.asarray(Y)[idx], Z[idx] # 按密度排序所有数据# 绘制散点图,颜色表示密度img = ax.scatter(X,Y,c=Z, # 颜色值基于密度s=s, # 点的大小cmap=cmap, # 颜色映射**kwargs) # 其他可选参数# 设置坐标轴范围ax.set_xlim(xlim)ax.set_ylim(ylim)# 添加坐标轴标签(如果指定)if xlabel:ax.set_xlabel(xlabel)if ylabel:ax.set_ylabel(ylabel)if title:ax.set_title(title)# 添加颜色条(如果启用)if cbar:cbar = plt.colorbar(img) # 创建颜色条cbar.ax.tick_params(labelsize=5) # 设置颜色条刻度标签的大小# 如果图形是新创建的,处理保存和显示逻辑if make_fig:if save: # 如果需要保存图形plt.savefig(save_path + 'DensityScatter_' + note + '.png',format='png',dpi=300,bbox_inches='tight') # 紧凑布局if show: # 如果需要显示图形plt.tight_layout() # 自动调整子图参数plt.show() # 显示图形plt.close() # 关闭图形释放内存# 返回坐标轴对象return ax# 绘制相关性矩阵图def plot_corr_matrix(id_data,id_label=None,ids=None,xlim=[None, None],ylim=[None, None],pair_corr=None,corr='Spearman',fig_scale=1,cell_size=1,label_color='black',text_color='black',scatter_style='dot',ms=1,mfc='k',mec='k',alpha=0.5,bins=20,xscale='linear',yscale='linear',basex=None,basey=None,cbar=True,cmap='Reds',vmin=0.1,vmax=0.9,save=False,save_path='./',save_type='png',show=True,title=None,cbar_label=None,note=''):# 如果未指定ids,则使用id_data的所有键并排序if ids is None:ids = sorted(id_data.keys())# 如果未指定id_label,则创建默认标签(将id转为字符串)if id_label is None:id_label = {id: str(id) for id in ids}# 获取数据数量(即要绘制的变量个数)data_num = len(ids)# ---- 计算图形尺寸 ----# 计算每个单元格的宽度和高度(基于缩放因子)cell_width = cell_size * fig_scalecell_height = cell_size * fig_scale# 设置图形边距left = 0.1 * fig_scaleright = 0.1 * fig_scalebottom = 0.1 * fig_scaletop = 0.1 * fig_scalewspace = 0.2 * fig_scalehspace = 0.2 * fig_scale# 如果需要颜色条,增加右侧边距if cbar:right += wspace + 0.3 * cell_size * fig_scale# 如果需要标题,增加顶部边距if title is not None:top += hspace + 0.3 * cell_size * fig_scale# 设置网格的行列数(N x N 矩阵)nrows = data_numncols = data_num# 计算总图形宽度和高度fig_width = cell_width * ncols + wspace * (ncols - 1) + left + rightfig_height = cell_height * nrows + hspace * (nrows - 1) + top + bottom# 创建图形和子图网格fig, axes = plt.subplots(nrows=nrows,ncols=ncols,figsize=(fig_width, fig_height))# 调整子图布局参数fig.subplots_adjust(left=left / fig_width,bottom=bottom / fig_height,right=1.0 - right / fig_width,top=1.0 - top / fig_height,wspace=wspace / cell_width,hspace=hspace / cell_height)# 初始化img变量(用于颜色条)img = None# 遍历所有子图位置for i in range(data_num):for j in range(data_num):# 获取当前单元格对应的两个ID和数据id1, id2 = ids[i], ids[j]data1, data2 = id_data[id1], id_data[id2]label1, label2 = id_label[id1], id_label[id2]# 获取当前坐标轴对象ax = axes[i, j]# 下三角区域(i > j):绘图if i > j:# 点状散点图样式if scatter_style == 'dot':ax.plot(data1, data2, 'k.',ms=ms, mfc=mfc, mec=mec, alpha=alpha)# 二维直方图样式elif scatter_style == 'histogram':ax.hist2d(data1, data2,range=[xlim, ylim],bins=bins)# 密度散点图样式elif scatter_style == 'density':density_scatter(data1, data2,cbar=False,xlim=xlim,ylim=ylim,ax=ax)# 设置坐标轴范围ax.set_xlim(xlim)ax.set_ylim(ylim)# 设置x轴刻度类型if xscale == 'log':if basex is None:ax.set_xscale('log')else:ax.set_xscale('log', base=basex)else:ax.set_xscale(xscale)# 设置y轴刻度类型if yscale == 'log':if basey is None:ax.set_yscale('log')else:ax.set_yscale('log', base=basey)else:ax.set_yscale(yscale)# 调整刻度标签显示:只显示最左边和最下边的标签if j > 0 and i < data_num - 1:ax.tick_params(axis='both', labelbottom=False, labelleft=False)if j == 0 and i < data_num - 1:ax.tick_params(axis='x', labelbottom=False)if j > 0 and i == data_num - 1:ax.tick_params(axis='y', labelleft=False)# 对角线区域(i == j):显示变量标签elif i == j:ax.text(4.5, 4.5, label1,color=label_color,ha="center",va="center",fontsize=10,weight='bold')ax.set_xlim([0, 9])ax.set_ylim([0, 9])ax.set_axis_off() # 隐藏坐标轴# 上三角区域(i < j):显示相关系数else:if pair_corr is None:if corr == 'Spearman':value = stats.spearmanr(data1, data2,nan_policy='omit')[0]elif corr == 'Pearson':value = stats.pearsonr(data1, data2)[0]else:value = pair_corr[(id1, id2)]# 创建10x10矩阵(用于显示颜色块)matrix = np.full((10, 10), value)img = ax.imshow(matrix,cmap=cmap,vmin=vmin,vmax=vmax,origin='lower')# 在颜色块上显示相关系数值ax.text(4.5, 4.5, str(round(value, 2)),ha="center",va="center",fontsize=10,color=text_color,weight='bold')# 设置显示范围并隐藏所有刻度ax.set_xlim([0, 9])ax.set_ylim([0, 9])ax.tick_params(axis='both',bottom=False, top=False,left=False, right=False,labelbottom=False,labelleft=False)# ---- colorbar ----if cbar and img is not None:# 创建网格布局来放置颜色条gs = gridspec.GridSpec(nrows=3,ncols=2,width_ratios=[1.0 - 0.5 * right / fig_width,0.5 * right / fig_width],height_ratios=[0.1, 2, 1],left=left / fig_width,bottom=bottom / fig_height,right=1.0 - left / fig_width,top=1.0 - top / fig_height)# 创建颜色条坐标轴cax = fig.add_subplot(gs[1, 1])cb = fig.colorbar(img, cax=cax)# 设置颜色条标签if cbar_label is None:cbar_label = corr + ' correlation'cax.set_ylabel(cbar_label,rotation=-90,va="bottom",fontsize=10)# 图片标题if title is not None:# 创建网格布局来放置标题gs = gridspec.GridSpec(nrows=2,ncols=1,height_ratios=[top / fig_height,1.0 - top / fig_height])tax = fig.add_subplot(gs[0, 0])tax.text(0, 0, title,ha="center",va="center",fontsize=20)tax.set_axis_off()# 保存图形if save:fname = save_path + f"Corr_matrix_{note}.{save_type}"plt.savefig(fname, dpi=1000, bbox_inches='tight')# 显示图形if show:plt.show()# 关闭图形plt.close()
绘图 - 彩虹色
plot_corr_matrix(dkey_data,dkey_label,ids=dkey_list,scatter_style='density',cmap='jet',fig_scale=0.5,vmin=0.1,vmax=0.8,cbar=True,save_path='./',save_type='png',save=True)
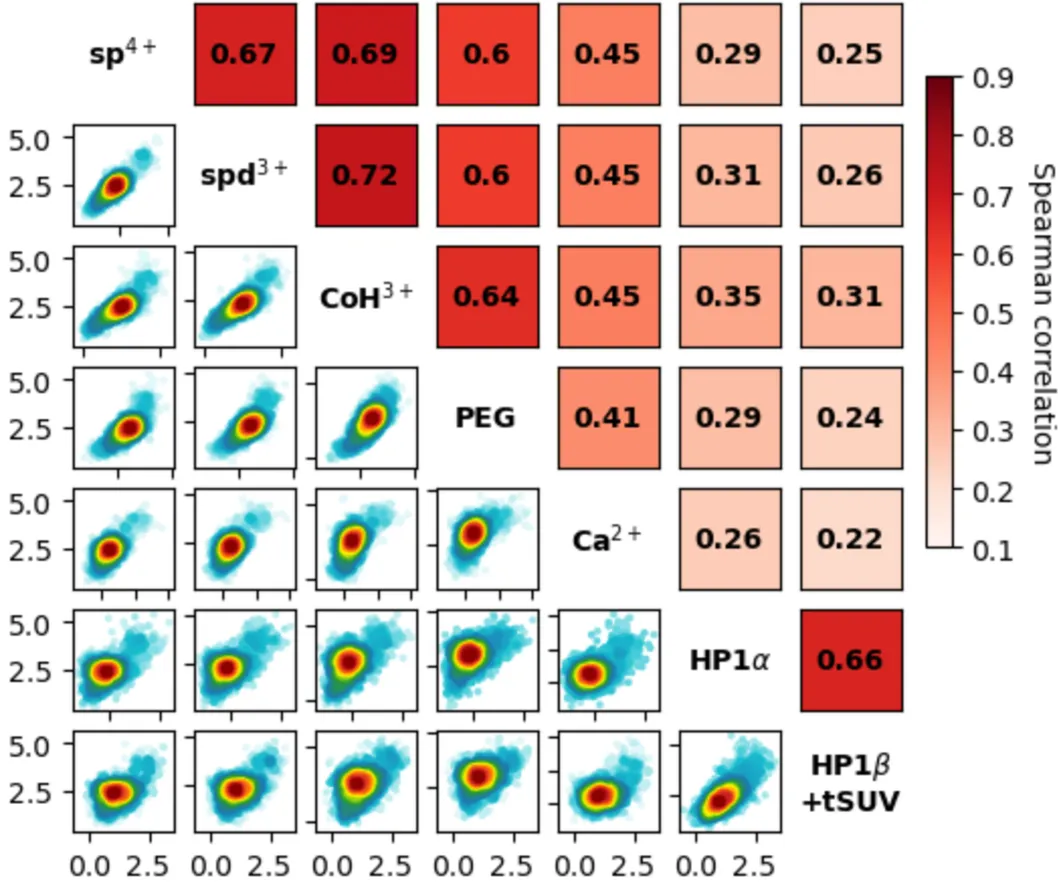
绘图 - 红色
plot_corr_matrix(dkey_data,dkey_label,ids = dkey_list,scatter_style='density',fig_scale=0.5,cbar=True,save_path='./',save=True)
更多相关性矩阵图的复现案例:
SCI 复现 | 相关性矩阵图(相关系数+散点图+对角直方图)

获取 .ipynb 格式绘图代码、测试数据和运行环境,后台回复关键词: 260120_density_corr_matrix_py
