我的Python100天打卡:56/100
- 2026-01-23 06:03:53
我的Python100天打卡:56/100
挑战100天持续练习Python 今天是第56天 --- 

3️⃣ 代码练习及#完整代码:(附上自己思考过程的注释) 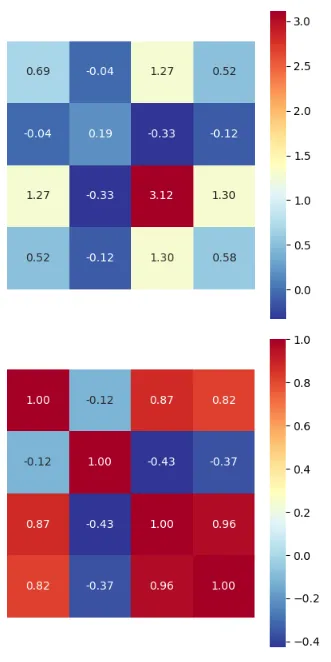
#鸢尾花数学大系

上次笔记,完成了第十五章Numpy的常见运算的前两小节部分。
今天继续挑战第十五章,具体内容包括:
15.3 使用Numpy进行统计运算(含完整代码)
15.4 Numpy库中的常见函数
--
15.3 使用Numpy进行统计运算
1️⃣进行写代码之前,先了解Numpy的统计运算要解决的问题场景,以及对应的工具:
(1)找最大/最小值:.max() .min()
(2)计算方差:np.var()
(3)计算标准差:np.std()
(4)计算协方差:np.cov()
(5)计算相关系数:np.corrcoef()
2️⃣统计运算常用到“总体方差”和“样本方差”,计算公式如下:

“总体方差”和“样本方差”的差异,通俗解释如下:

# 代码 15.1 Numpy中的统计运算import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.datasets import load_iris# 导入鸢尾花数据iris = load_iris()iris_data_array = iris.data# 为了更好地学习代码,下面我将逐行用自己的话进行注释,检测理解情况print (iris_data_array.max()) # 使用numpy中的.max()方法,求出整个矩阵的最大值print (iris_data_array.max(axis = 0)) # 使用numpy中的.max()方法,并限定axis=0的参数,求出每一列的最大值print (iris_data_array.max(axis = 1)) # 同上,限定axis=1参数,求出每一行的最大值# numpy.argmax() :返回数组中最大元素的索引(位置)print (np.argmax(iris_data_array, axis = 0)) # 使用np.argmax()方法,求出每列最大值的位置print (np.argmax(iris_data_array, axis = 1)) # 使用np.argmax()方法,限定axis=1参数,求出每行最大值的位置# numpy.average() :计算数组的加权平均值print (np.average(iris_data_array, axis = 0)) # 计算每列均值print (np.average(iris_data_array, axis = 1)) # 计算每行均值# 计算每一列的总体方差(分母=n)# np.var(): 计算数组中元素的方差,默认自由度ddof=0 (ddof = delta degrees of freedom)# 更多关于方差的练习,在前面章节的笔记中也有记录print(np.var(iris_data_array, axis = 0 )) # numpy默认分母为n(方差计算公式)# 注意:和下方“样本方差”的代码相比,这里省略了“ddof = 0”的设定,也就是取默认值即可# 计算每一列的样本方差(分母=n-1)print(np.var(iris_data_array, axis = 0, ddof = 1))# 计算每一列的标准差# np.std():计算标准差print(np.std(iris_data_array, axis = 0))# 计算协方差矩阵;注意“转置”的要求# np.cov(): 计算数组中元素的协方差矩阵,默认自由度ddof为=0SIGMA = np.cov(iris_data_array.T, ddof = 1) # 我的理解:1. 使用data.T转置; 2. 使用ddof=1修改默认自由度print(SIGMA)# 把上述的协方差矩阵可视化:fig, ax = plt.subplots(figsize = (5,5))sns.heatmap(SIGMA, cmap = 'RdYlBu_r', annot = True, ax = ax, fmt = '.2f', square = True,xticklabels = [], yticklabels = [], cbar = True)# 计算相关系数矩阵;注意“转置”的要求# np.corrcoef(): 计算数组中元素的“相关系数”矩阵,自由度ddof没有影响;因为相关系数是协方差除以各自标准差的乘积,而其中除以n或n-1的因子在分子和分母中会相互抵消。CORR = np.corrcoef(iris_data_array.T)print(CORR)# 把上述协方差矩阵可视化:fig, ax = plt.subplots(figsize = (5,5))sns.heatmap(CORR, cmap = 'RdYlBu_r', annot = True, ax = ax, fmt = '.2f', square = True,xticklabels = [], yticklabels = [], cbar = True)
4️⃣可视化运行结果:

-
15.4 Numpy库中的常见函数
1️⃣先用一段代码定义“可视化一元函数”:
# 代码15.2 自定义可视化函数import numpy as npimport matplotlib.pyplot as plt# 自定义可视化函数def visualize_fx(x_array, f_array, title, step = False):fig, ax = plt.subplots(figsize = (5,5))ax.plot([-5,5], [-5,5], c = 'r', ls = '--', lw = 0.5)if step: # 这是什么意思?ax.step(x_array, f_array)else:ax.plot(x_array, f_array)ax.set_xlim(-5,5)ax.set_ylim(-5,5)ax.axvline(0, c = 'k')ax.axhline(0, c = 'k')ax.set_xticks(np.arange(-5,5+1))ax.set_yticks(np.arange(-5,5+1))ax.set_xlabel('x')ax.set_ylabel('f(x)')plt.grid(True)ax.set_aspect('equal', adjustable = 'box')fig.savefig(title + '.svg', format = 'svg') # 好优雅的保存图片文件的代码,简洁易懂
2️⃣再用一段代码,给出函数后,调用visualize_fx进行可视化:
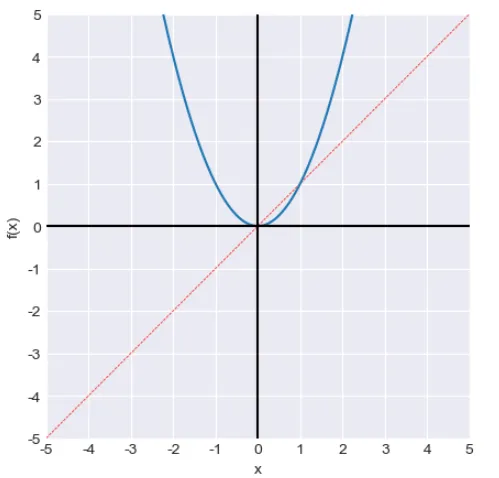
# 代码15.3 提供一元函数,并调用已写好的函数进行可视化:# 幂函数power, p=2x_array = np.linspace(-5, 5, 1001)f_array = np.power(x_array, 2)visualize_fx(x_array, f_array, '幂函数')
3️⃣运行结果:

--
心得:今天的笔记有点短,身体休息了一阵子,今天重新拾起书本,记录笔记。
果然还是写笔记的过程,学得更加心安。
写笔记不一定是学习效率最快的,但一定是最适合我现在当下的能力的。
重在坚持。
加油~!
写于2026年1月21日16:41:23
--
本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。
