编辑:Peter 作者:Peter
今天给大家介绍7种插值方法:线性插值、抛物插值、多项式插值、样条插值、拉格朗日插值、牛顿插值、Hermite插值,并提供Python实现的代码过程。
导入库
导入数据处理和建模需要的库:
import numpy as npimport pandas as pdimport randomimport matplotlib.pyplot as plt%matplotlib inlineplt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签plt.rcParams['axes.unicode_minus'] = False# 显示负号import warningswarnings.filterwarnings("ignore")
线性插值interp1d
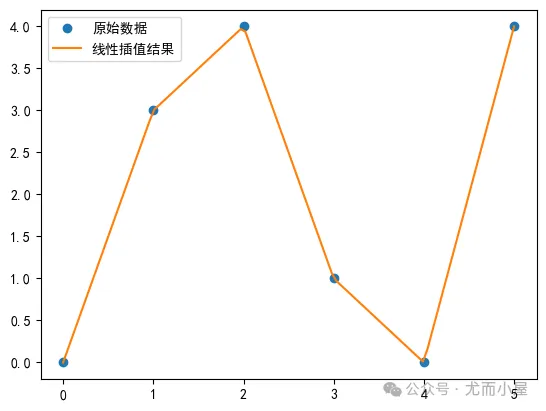
线性插值是一种数学方法,用于估计两个已知值之间的未知值。这种方法假设在这两个已知点之间的变化是线性的,即变化率是恒定的。线性插值因其简单和直观的特点,在多个领域如图像处理、数据分析等都有广泛的应用。
具体来说,线性插值的原理可以描述为:
确定已知点:需要有两个已知的数据点,通常表示为 (x0, y0) 和 (x1, y1)。
计算插值系数:这个系数定义为 ,其中 x 是要估计的值的位置。
应用线性插值公式:根据插值系数 α,可以使用公式 来计算 y 的值。这个公式说明了 y 的值是由 y0 和 y1 按照它们距离 x 的相对位置加权平均得到的。
扩展到多维空间:线性插值可以扩展到二维或三维空间,分别称为双线性插值和三线性插值。在二维空间中,首先沿着一个轴进行两次线性插值,然后再沿着另一个轴进行一次线性插值,从而得到最终的插值结果。
在实际应用中,线性插值常用于图像大小调整中的像素值估算,数据缺失时的合理补偿,以及数据放缩等情况。
由于其简单性,线性插值计算效率高,易于实现。然而,它基于线性变化的假设,对于非线性关系的数据,线性插值可能不会给出最准确的估计。在这些情况下,可能需要使用更高阶的插值方法,如多项式插值或样条插值等。
from scipy.interpolate import interp1dx = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])# 创建线性插值函数f = interp1d(x, y, kind='linear')# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = f(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='线性插值结果')# 添加图例plt.legend()# 显示图形plt.show()
抛物插值Parabolic interpolation
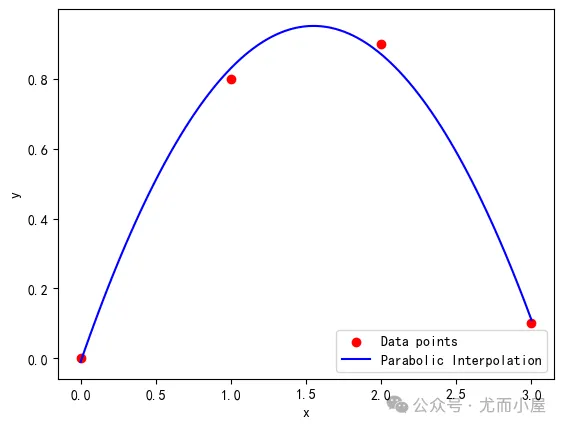
抛物插值,也称为二次插值,是一种多项式插值方法。这种方法利用已知的数据点来构造一个二次多项式,以此作为未知函数的近似。
import numpy as np import matplotlib.pyplot as plt # 数据点 x = np.array([0, 1, 2, 3]) y = np.array([0, 0.8, 0.9, 0.1]) # 使用numpy的polyfit函数进行二次拟合(即抛物插值),返回的是拟合多项式的系数 # 从最高次到最低次,例如对于ax^2 + bx + c,返回的是[a, b, c] coeffs = np.polyfit(x, y, 2) # 测试数据:x_min 和 x_max 之间取100个点 x_new = np.linspace(min(x), max(x), 100) # 生成一个更细粒度的x值数组用于插值 y_new = np.polyval(coeffs, x_new) # 拟合结果 # 绘制原始数据点和插值曲线 plt.scatter(x, y, label='Data points', color='red') plt.plot(x_new, y_new, label='Parabolic Interpolation', color='blue') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.show()
多项式插值BarycentricInterpolator
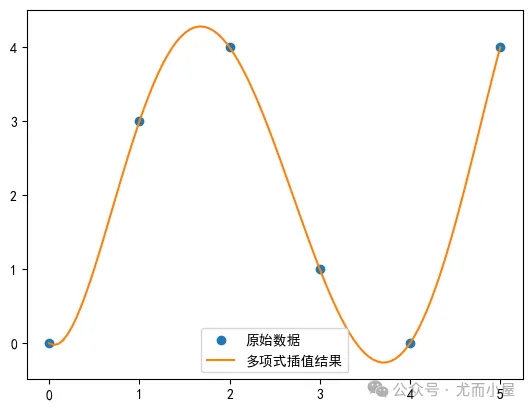
多项式插值是一种数学方法,用于根据已有的数据点找到一个多项式函数,使得该函数通过所有给定的数据点。
from scipy.interpolate import BarycentricInterpolatorx = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])# 创建多项式插值函数f = BarycentricInterpolator(x, y)# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = f(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='多项式插值结果')# 添加图例plt.legend()# 显示图形plt.show()
样条插值CubicSpline
样条插值是一种数值分析技术,用于通过一组给定的数据点构造一个平滑的曲线。它的基本思想是在数据点之间构建多项式函数,这些函数在相邻数据点处具有连续的一阶导数,从而形成一条光滑的曲线。
基于CubicSpline
from scipy.interpolate import CubicSpline # 3次样条插值CubicSpline# 示例数据x = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])# 创建三次样条插值函数cs = CubicSpline(x, y)# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = cs(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='样条插值结果')# 添加图例plt.legend()# 显示图形plt.show()
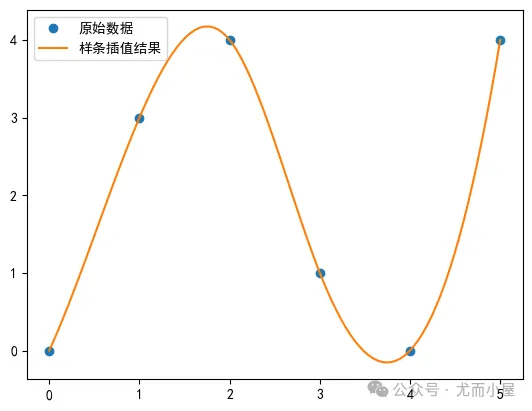
基于interp1d(kind='cubic')
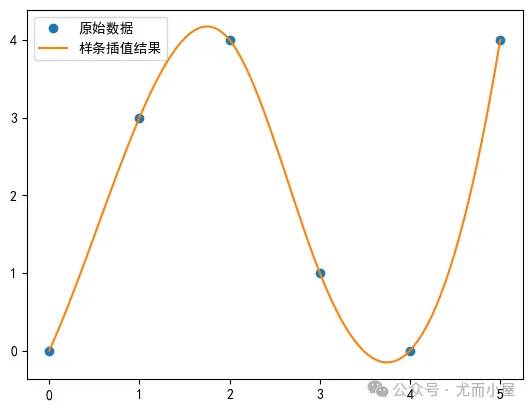
from scipy.interpolate import interp1dx = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])# 创建线性插值函数f = interp1d(x, y, kind='cubic') # 指定为cubic:3次# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = f(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='样条插值结果')# 添加图例plt.legend()# 显示图形plt.show()
拉格朗日插值法Lagrange
拉格朗日插值也是属于一种多项式插值,其原理是通过多个采样点构造一个高次多项式来近似替代
from scipy.interpolate import lagrange# 示例数据x = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])# 创建拉格朗日插值函数f = lagrange(x, y)# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = f(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='拉格朗日插值结果')# 添加图例plt.legend()# 显示图形plt.show()
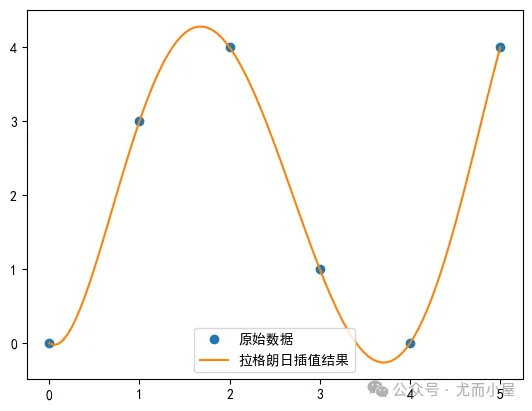
牛顿插值法newton
牛顿插值法的基本思想是利用差分和差商的概念来构建插值多项式。差商是一种特殊的除法运算,用于计算函数值之间的差异,而差分则是差商的离散形式。
牛顿插值多项式的构造是通过计算零阶到n阶的差商来实现的。这些差商可以用来逐步构建插值多项式,每次增加一个项,直到达到所需的次数
import numpy as npdefnewton_interpolation(x, y):""" 牛顿插值法 x: 已知点的横坐标列表 y: 已知点的纵坐标列表 return: 插值多项式函数 """ n = len(x) # 初始化差商表 f = [[0] * n for _ in range(n)] # n*n的全0维数组for i in range(n): f[i][0] = y[i] # 将已知点的纵坐标赋值给差商表的第一列 for j in range(1, n): # j表示差商的阶数for i in range(n - j): # i用于遍历每行的起始位置 f[i][j] = (f[i + 1][j - 1] - f[i][j - 1]) / (x[i + j] - x[i]) # 计算差商# 构造插值多项式函数defP(t): result = 0# 初始值for i in range(n): # 双重循环 temp = 1# 临时变量,用于计算(t-x[j])的乘积 for j in range(i): temp *= (t - x[j]) result += f[0][i] * temp # 将差商与(t-x[j])的乘积累加到result中 return resultreturn P
# 示例数据x = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])P = newton_interpolation(x,y)# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = P(x_new)
# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='牛顿插值结果')# 添加图例plt.legend()# 显示图形plt.show()
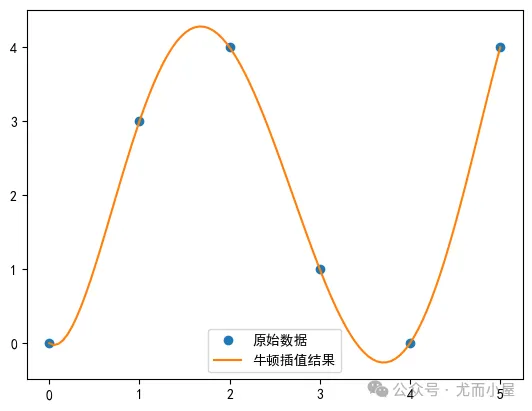
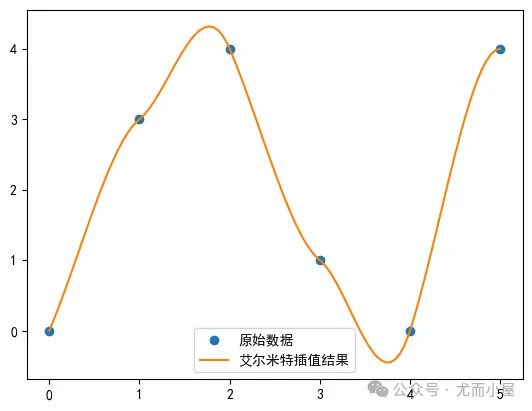
艾尔米特插值法Hermite
埃尔米特插值是另一类插值问题,这类插值在给定的节点处,不但要求插值多项式的函数值与原函数值相同。
同时还要求在节点处,插值多项式的一阶直至指定阶的导数值,也与被插函数的相应阶导数值相等,这样的插值称为埃尔米特(Hermite)插值。
import numpy as npfrom scipy.interpolate import CubicHermiteSpline# 示例数据x = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 3, 4, 1, 0, 4])dy = np.array([3, 1, -3, -1, 4,0])# 创建Hermite插值函数f = CubicHermiteSpline(x, y, dy)# 计算插值结果x_new = np.linspace(0, 5, 100)y_new = f(x_new)# 绘制x和y的图形plt.plot(x, y, 'o', label='原始数据')# 绘制x_new和y_new的图形plt.plot(x_new, y_new, '-', label='艾尔米特插值结果')# 添加图例plt.legend()# 显示图形plt.show()