期刊图复现 | Python 画 SHAP 环形蜂巢图 + 玫瑰花图

很多时候做完模型训练后，会遇到两个“解释性”层面的需求：

1. 特征到底谁更重要？（全局重要性排序）
2. 重要性背后到底发生了什么？（同一特征在不同样本上的贡献分布、正负方向、以及与特征取值高低的关系）

传统条形图往往只能回答第 1 个问题；而 SHAP summary/beeswarm 虽然能回答第 2 个问题，但在做“图形化呈现”时不够紧凑。本文基于这个思路，把这两个问题合并到一张图里：

复现期刊及图片

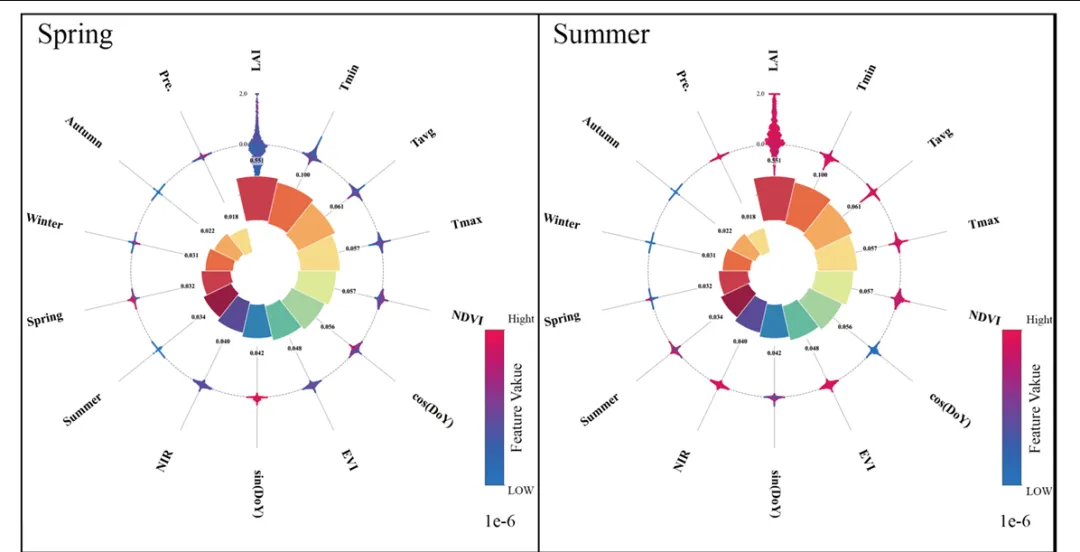
复现结果

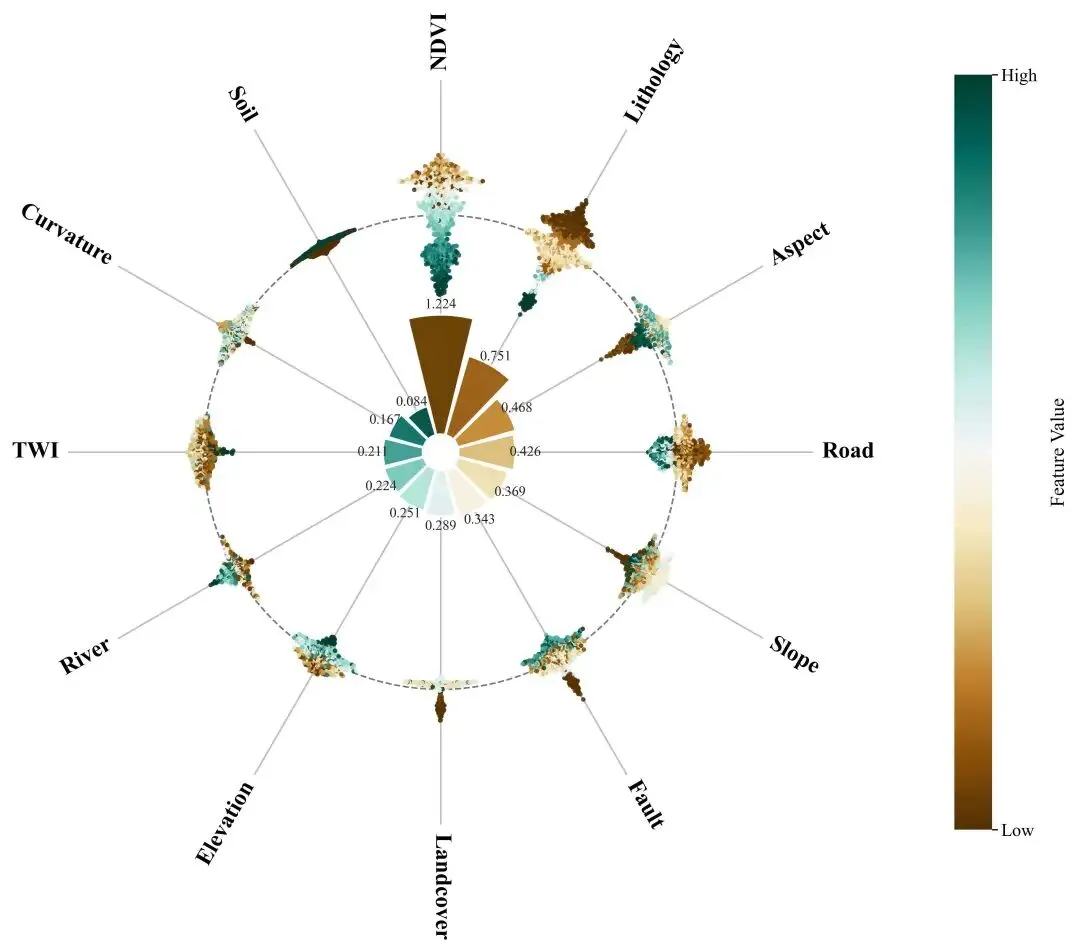
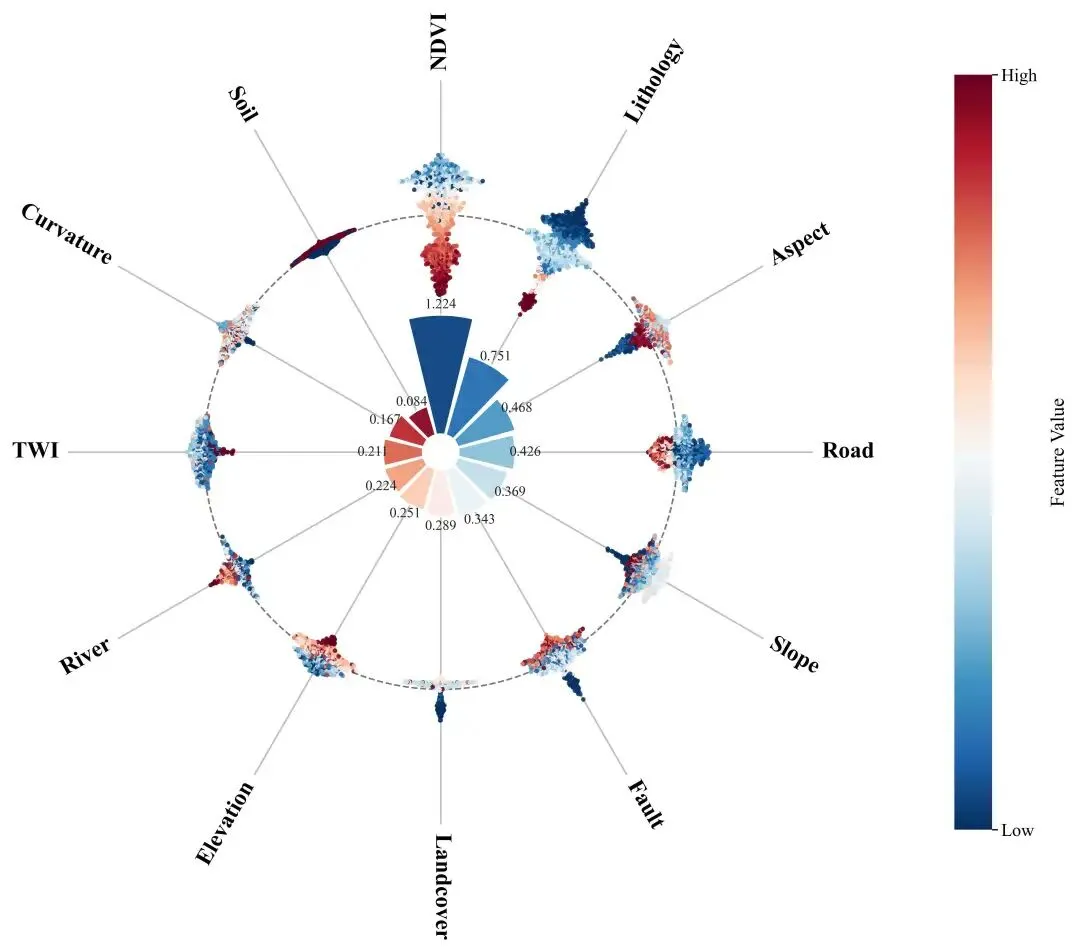
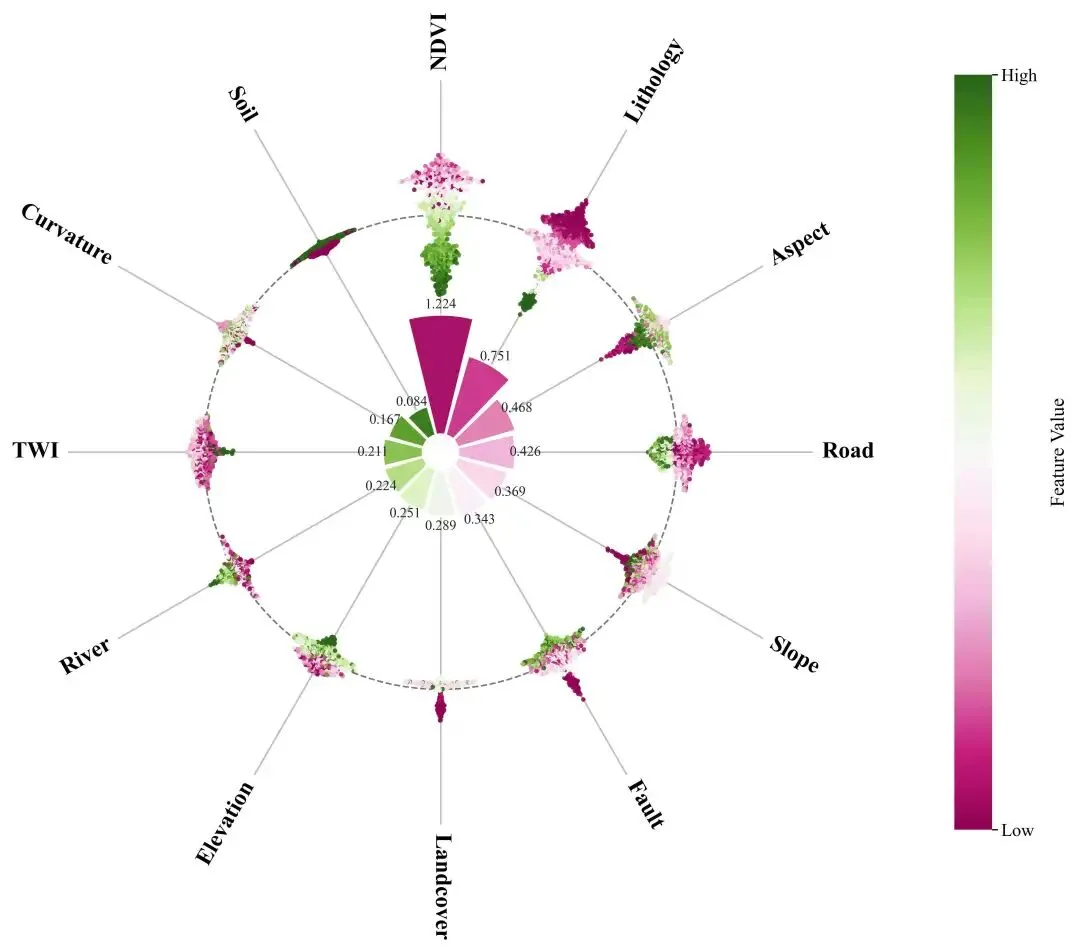
• 内圈玫瑰花图（环形柱）：用 mean(|SHAP|) 表达全局重要性，配合数值标注，直观看到“谁更重要”。
• 外圈环形蜂巢图（极坐标 beeswarm）：把每个样本的 SHAP 值映射到半径方向，再在角度方向做“蜂群抖动”防重叠；颜色用原始特征值（Low→High）映射，直观看到“高值/低值分别倾向推动正类还是负类”。

这类“内圈总结 + 外圈分布”的组合图特别适合论文插图或汇报：读者第一眼看重要性，第二眼看机制，而且画面非常紧凑。

为了让读者快速“读懂图”，建议你在文章/图注里给出一行读图规则：“看内圈花瓣高度=重要性；看外圈点在虚线圆内外=贡献正负；看点的颜色=特征取值高低（Low→High）。”

# 01_全局配置与参数from __future__ import annotationsfrom pathlib import Pathimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport shapimport xgboost as xgbplt.rcParams["font.family"] = "Times New Roman"plt.rcParams["axes.unicode_minus"] = Falseplt.rcParams["figure.dpi"] = 300plt.rcParams["savefig.bbox"] = "tight"plt.rcParams["font.size"] = 12RANDOM_SEED = 42CSV_FILE = "分类样本.csv"TARGET_COL = "label"OUTPUT_DIR = Path("images")  # 输出目录（自动创建）CLASS_INDEX_FOR_SHAP = 0# 多分类时选哪一类的 SHAPTOP_N = None# 只画前 N 个特征（None=全部）COLOR_SCHEMES = [    ("RdBu_r", "RdBu_r"),    ("Viridis", "viridis"),    ("YlGnBu", "YlGnBu"),]

1) 数据与模型：把分类问题“标准化”到可解释的输入输出

想画 SHAP 图，第一步不是“画”，而是把输入和输出变得稳定且可复现：特征矩阵必须是纯数值（分类变量要 one-hot），标签必须是可控的整数编码，模型要固定随机种子。这样做的好处是：

• 你后续计算的 SHAP 值维度稳定（(n_samples, n_features)），不会因为某一列是字符串而报错。
• 同一份数据重复跑出来的结果一致（对比实验、换配色、换图形参数才有意义）。
• 多分类场景下，你能明确“我现在解释的是哪一类（class）”，避免把不同类别的贡献混在一张图里产生误读。

这篇文章以 XGBoost 分类器为例：它在科研场景里足够常见、效果稳定，而且 shap.TreeExplainer 对树模型速度非常快，适合做可视化。

另外两个常见“坑”也建议提前处理：（1）缺失值：XGBoost 可以处理缺失，但你的 one-hot 后矩阵如果混入 object 类型或 NaN 传播到字符串列，后面会很难排查；稳妥做法是先把数据清洗到“纯数值”。（2）列名与可读性：如果后续要发表/展示，建议把列名提前改成简洁但不含歧义的英文缩写；本文脚本也支持把长列名映射为 F1..Fn（便于排版），同时导出映射表。

defto_numeric_matrix(X: pd.DataFrame) -> pd.DataFrame:    non_numeric = [c for c in X.columns ifnot pd.api.types.is_numeric_dtype(X[c])]return pd.get_dummies(X, columns=non_numeric, drop_first=False) if non_numeric else Xdata = pd.read_csv(CSV_FILE)X = to_numeric_matrix(data.drop(columns=[TARGET_COL]))# 标签编码：把任意字符串/整数标签统一成 0..K-1，并保留映射关系y_raw = data[TARGET_COL]y, y_classes = pd.factorize(y_raw, sort=True)print("类别映射:", dict(enumerate([str(v) for v in y_classes])))n_classes = len(y_classes)objective = "binary:logistic"if n_classes == 2else"multi:softprob"eval_metric = "logloss"if n_classes == 2else"mlogloss"model = xgb.XGBClassifier(    n_estimators=300,    max_depth=4,    learning_rate=0.05,    subsample=0.8,    colsample_bytree=0.8,    random_state=RANDOM_SEED,    n_jobs=-1,    objective=objective,    eval_metric=eval_metric,    num_class=(n_classes if n_classes > 2elseNone),)model.fit(X, y)

2) 计算 SHAP：把“黑箱预测”拆成逐特征的加性贡献

在树模型里，SHAP 的核心输出是：对每个样本、每个特征，给一个实数贡献值（可正可负）。在分类任务中要注意两点细节：

1. 二分类 vs 多分类的返回格式差异在一些版本组合下，explainer.shap_values(X) 可能返回 list（长度=类别数），也可能直接返回 array。稳妥做法是：检测 list 就按 CLASS_INDEX_FOR_SHAP 取某一类再画。

2. 把“重要性”定义成可排序的标量为了做内圈“玫瑰花柱”，需要每个特征一个标量。最常用也最稳健的是：mean(|SHAP|)。它忽略正负方向，回答“这个特征对模型输出的平均影响强度有多大”。

做完这一步，你会得到两套信息：

• mean_abs：长度为 n_features 的一维数组，给内圈排序/花瓣高度用。
• shap_values：形状 (n_samples, n_features) 的二维数组，给外圈蜂巢点阵用（看到分布、方向、异质性）。

解释上可以把它理解成一种“可加性分解”：模型对某个样本的输出，是“基线值 + 各特征贡献”的叠加。mean(|SHAP|) 只是在全体样本上把贡献的强度取了平均，因此特别适合做“全局重要性”；而外圈保留每个样本点，适合回答“在不同样本上这个特征到底怎么起作用”。

explainer = shap.TreeExplainer(model)shap_values = explainer.shap_values(X)# 兼容二/多分类：如果是 list，则选定一个类别来画if isinstance(shap_values, list):    shap_values = shap_values[CLASS_INDEX_FOR_SHAP]shap_values = np.asarray(shap_values, dtype=float)  # (n_samples, n_features)mean_abs = np.mean(np.abs(shap_values), axis=0)order = np.argsort(mean_abs)[::-1]  # 重要性从高到低if TOP_N isnotNone:    order = order[: int(TOP_N)]X_sel = X.iloc[:, order].to_numpy(dtype=float, copy=False)shap_sel = shap_values[:, order]mean_abs_sel = mean_abs[order]feature_names = [str(c) for c in X.columns]labels_sel = [feature_names[i] for i in order]

3) 玫瑰花图（内圈）：用极坐标环形柱表达全局重要性

“玫瑰花图”本质是极坐标柱状图：每个特征占一个角度扇区（theta），柱子的高度表示该特征的重要性（这里用 mean(|SHAP|)）。为了画得更“出版级”，这里有几个关键处理：

• 高度缩放：重要性往往差异很大，直接用原值画，弱特征会几乎看不见。可以先把 mean_abs 线性归一到 [0,1]，再映射到 [MIN_H, MAX_H] 的柱高范围。
• 最短花瓣高度：MIN_H 不是“美化”，它是为了避免某些特征在图上完全消失，从而导致读者误以为“没有该特征”。
• 数值标注：公众号读者通常更希望“看见数值”，而不只是一堆颜色。每个花瓣顶部标注 mean(|SHAP|)，图的解释成本会显著下降。

如果你希望“花瓣颜色也表达信息”，常见做法是用同一 colormap 对花瓣按重要性上色（越重要越深），但本文脚本把花瓣颜色做成均匀渐变，更多是为了增强层次与美观；真正的“信息承载”交给外圈颜色（特征值），避免信息冲突。