叶老师先讲到集合的势,即设A与B是两个集合,如果存在一个由A到B上的一对一的映射,我们就称集A与集B有“相同的势”,或者说A与B等价,用A~B来表示。然后他给出了该定义的关系具有这几种性质:自反性(A~A),对称性(若A~B,则B~A),传递性(若A~B且B~C,则A~C)。
接着,叶老师讲到整数集的可数性,他证明了“整数的全体A是可数集”、“(0,1)与[0,1]有相同的势”、“一个可数集A的每一个无限子集是可数集”。随后他讲解并证明了“设{En},n=1,2,3,...,是一列至多可数集,令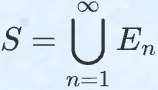 ,那么S是至多可数集”,再使用该结论去证明“R中的全体有理数是可数的”,然后他引入对Cantor三分法的介绍并使用该方法反证了[0,1]上的全体实数是不可数的。
,那么S是至多可数集”,再使用该结论去证明“R中的全体有理数是可数的”,然后他引入对Cantor三分法的介绍并使用该方法反证了[0,1]上的全体实数是不可数的。