Python | XGBoost+SHAP 可解释性分析回归预测及可视化算法!!

大家好，我是小寒

今天给大家分享机器学习中的一个关键概念，SHAP

SHAP（Shapley Additive Explanations）是一个用于机器学习模型解释的框架，用于解释模型的预测结果。

SHAP 的核心思想源自于博弈论中的 Shapley值（Shapley Value），它通过量化每个特征对预测结果的贡献，来帮助理解复杂模型的预测依据。

SHAP可以应用于各种类型的模型，包括黑盒模型（如深度学习、随机森林等），提供模型可解释性。

Shapley 值的基本概念

在博弈论中，Shapley 值用于分配合作博弈中的总收益给参与者。假设有一组玩家，每个玩家根据他们的贡献分配一个价值。Shapley 值的核心是根据每个玩家在不同合作组合中的边际贡献来计算其公平的分配。

想象一个场景：三位球员（特征 ）组队参加比赛，最后球队赢得了 100 分（模型预测值）。Shapley 的任务就是通过数学方法计算出，这 100 分里，每一位球员分别贡献了多少？

在机器学习模型中，参与者就是各个特征，收益就是模型的预测结果，Shapley 值用来衡量每个特征对最终预测的贡献度。

Shapley 值的数学公式

设模型的预测是由一组特征   组成的，模型的预测结果为 ，而我们想计算某个特征  对模型预测的贡献 。

 的计算考虑了特征  在所有可能的特征组合中带来的边际贡献。

其数学表达式为

其中

•  是所有特征的集合， 为总特征数。
•  是特征集  中除去特征  后的任意子集。
•  是模型在特征子集  上的预测值。
•  是加入特征  后产生的边际贡献。
•  是加权系数 ，代表了该子集出现的概率权重。

加性解释模型

SHAP 属于加性解释模型。它将复杂的黑盒模型（如 XGBoost, LightGBM, 深度学习等）在某个样本上的预测值，拆解为各特征贡献值的线性加和。

对于一个特定的样本 ，我们将模型  简化为一个线性解释模型 ：

其中：

•  是解释模型。
•  是简化特征（1 表示特征存在，0 表示特征缺失）。
•  是基准值（通常是所有样本预测值的期望 ）。
•  就是第  个特征的 SHAP Value。

这种加性特性使得 SHAP 非常适用于模型的解释，因为它保证了所有特征的贡献之和等于模型的最终预测结果。

SHAP 的性质

1. 局部准确性

   所有特征的 SHAP 值之和加上基准值（模型在训练集上的平均预测值），等于该样本的实际预测值。

2. 缺失性：如果一个特征在某个样本中不存在或对预测没有贡献，它的 SHAP 值应为 0。

3. 一致性：如果模型发生了变化，使得某个特征的边际贡献增加了，那么该特征的 SHAP 值不应该减少。

SHAP 值计算的效率

计算精确的 Shapley 值需要穷举所有可能的特征子集，随着特征数的增加，计算量呈指数级增长，因此直接计算 Shapley 值对于大规模问题是不可行的。

为了解决这一问题，SHAP 提出了多种近似算法，包括

• Kernel SHAP：一种模型无关的方法。通过线性回归（Lasso）来近似估计 SHAP 值，适用于任何黑盒模型。
• Tree SHAP：专门为树模型（XGBoost, LightGBM, CatBoost, Random Forest）优化的算法。它利用树的结构，将计算复杂度从指数级降低到多项式级，计算速度极快。
• Deep SHAP：结合了 DeepLIFT 算法，专门用于神经网络。

SHAP 的可视化

SHAP 还提供了一些可视化工具，帮助用户理解特征重要性和贡献。

• Force Plot：解释单个样本。红色表示将预测值推高的特征，蓝色表示压低预测值的特征。
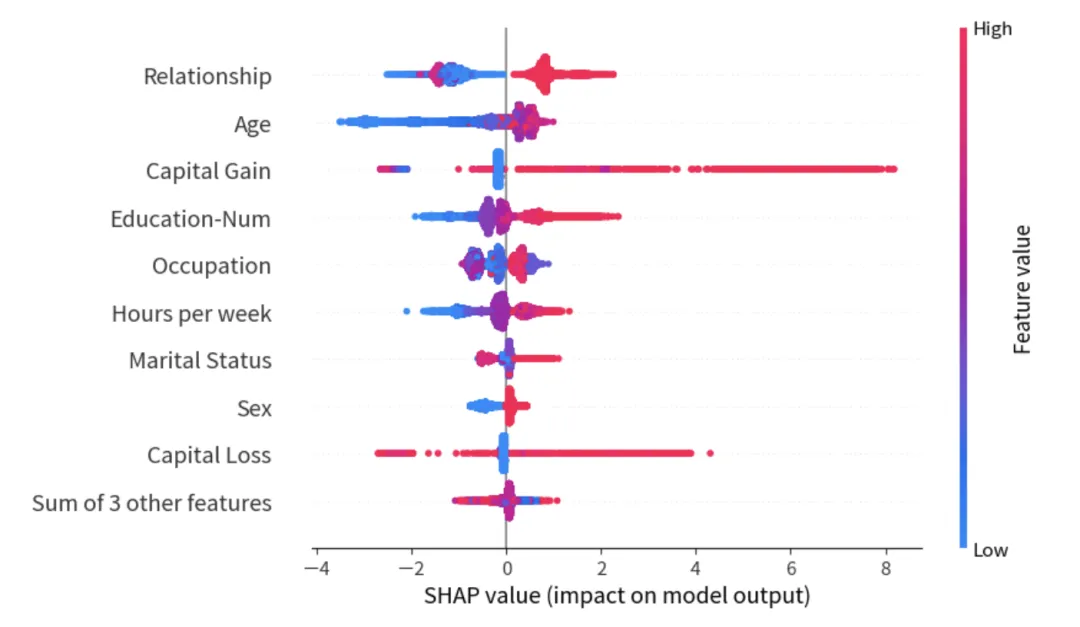
• Summary Plot：展示全局特征重要性。它不仅显示哪些特征重要，还显示特征取值高低对预测方向的影响。
• Dependence Plot：展示单个特征取值与 SHAP 值之间的非线性关系。
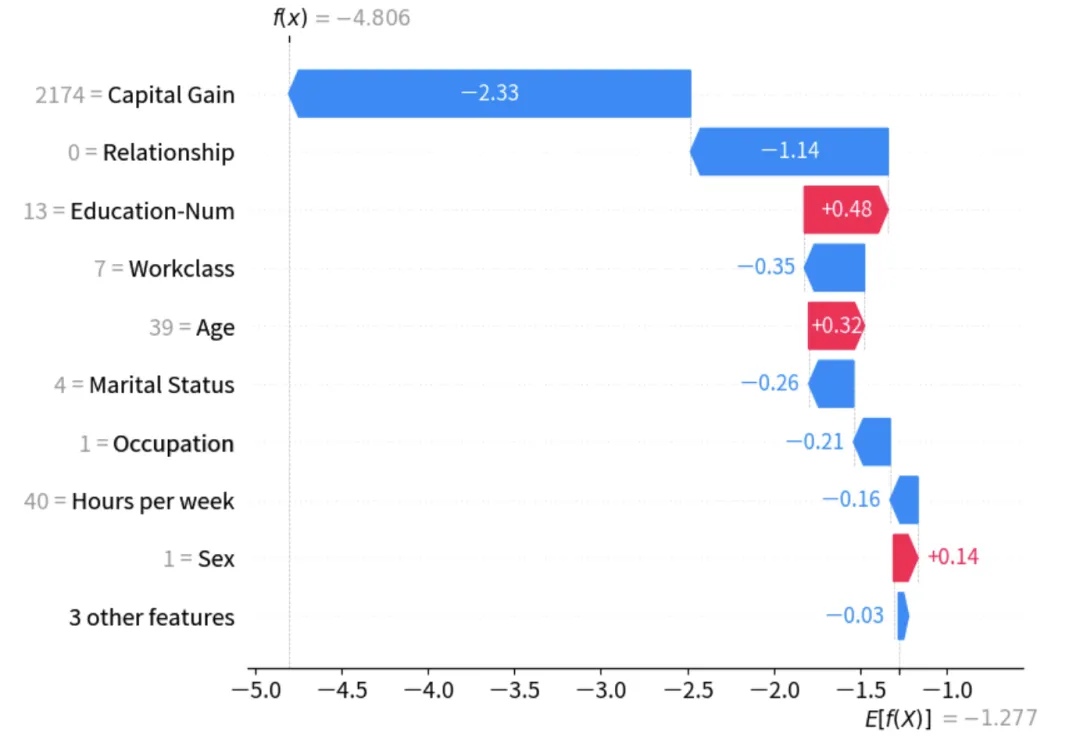
• Waterfall Plot：展示一个特定样本的预测路径。从期望值  开始，每一个特征如何一步步将预测值推向最终结果。

案例分享

以下是一个完整的示例代码，演示如何使用 shap 解释 Xgboost 算法。

import xgboostimport shapimport matplotlib.pyplot as plt# 1. 加载标准数据集 (SHAP 内置)X, y = shap.datasets.adult()# 2. 训练一个 XGBoost 模型# 在真实场景中，我们通常会进行训练/测试集拆分，这里为了演示直接拟合model = xgboost.XGBClassifier(n_estimators=100, max_depth=3).fit(X, y)# 3. 构建解释器 (Explainer)# 对于树模型，TreeExplainer 是计算效率最高且最准确的选择explainer = shap.TreeExplainer(model)# 4. 计算 SHAP Values# shap_values 包含了基准值 (base_value) 和每个样本的贡献值# 注意：在 0.50.0 版本中，返回的是一个 Explanation 对象，非常方便绘图shap_values = explainer(X)# --- 图像绘制 ---# 设置绘图风格plt.rcParams['figure.figsize'] = (10, 6)# 5. 绘制第一个样本的 Waterfall Plot# 它展示了模型如何从均值 E[f(X)] 推导至当前样本的预测值 f(x)print("正在生成瀑布图...")shap.plots.waterfall(shap_values[0], max_display=10)

# 6. 绘制 Summary Plot (全局解释)# 瀑布图看局部，Summary Plot 看整体特征趋势plt.figure()shap.plots.beeswarm(shap_values)plt.show()