七年级北师大版数学与 Python 编程融合学习方案

一、七年级（北师大版）数学+Python编程融合学习目录

（一）七年级上册

（二）七年级下册

二、将数学学习融入Python编程的核心方法

1. 以“验证/计算”为切入点，让编程服务于数学

      数学学习中大量的计算（如有理数运算、整式求值、几何面积）可以通过编程实现，既练习编程语法，又验证数学结果的正确性。

示例：学习一元一次方程时，编写解方程程序，让学生理解“移项→系数化为1”的逻辑，而非死记公式。

2. 以“可视化”破解抽象概念

       七年级数学的抽象知识点，如对顶角、邻补角、平行线判定、角度计算，用Python的turtle（绘图）可视化，降低理解难度。

      示例1：用turtle画对顶角、邻补角、平行线判定、角度计算。

# 例子1：绘制相交线，标注对顶角（简化版，已知一个角求对顶角）
import turtle
t = turtle.Turtle()
t.speed(2)

# 绘制相交线
t.forward(200)
t.backward(400)
t.forward(200)
t.right(60)  # 一个角为60°，对顶角也为60°，邻补角为120°
t.forward(200)
t.backward(400)

# 标注对顶角（60°）
t.penup()
t.goto(50, 30)
t.pendown()
t.write("60°", font=("Arial", 12))
t.penup()
t.goto(-50, -30)
t.pendown()
t.write("60°", font=("Arial", 12))

# 计算对顶角
angle = 60
vertical_angle = angle  # 对顶角相等
print(f"已知一个角为{angle}°，其对顶角也为{vertical_angle}°")

turtle.done()

# 例子2：平行线判定（同位角相等，两直线平行）
angle1 = float(input("请输入第一个同位角的度数："))
angle2 = float(input("请输入第二个同位角的度数："))

if abs(angle1 - angle2) < 0.001:
    print(f"两个同位角分别为{angle1}°和{angle2}°，度数相等")
    print("根据“同位角相等，两直线平行”，可判定这两条直线平行！")
else:
    print(f"两个同位角分别为{angle1}°和{angle2}°，度数不相等")
    print("根据“同位角相等，两直线平行”，无法判定这两条直线平行！")

# 例子3：用turtle绘制垂线，标注直角符号
import turtle
t = turtle.Turtle()
t.speed(2)

# 绘制一条水平线
t.forward(200)
t.backward(100)  # 回到线段中点

# 绘制垂线（右转90°）
t.right(90)
t.forward(100)
t.backward(200)

# 标注直角符号（简化版）
t.penup()
t.goto(-10, 10)
t.pendown()
t.setheading(45)
t.forward(15)

print("已绘制一条水平线和一条垂线，标注了直角符号（90°）")
turtle.done()
   运行：

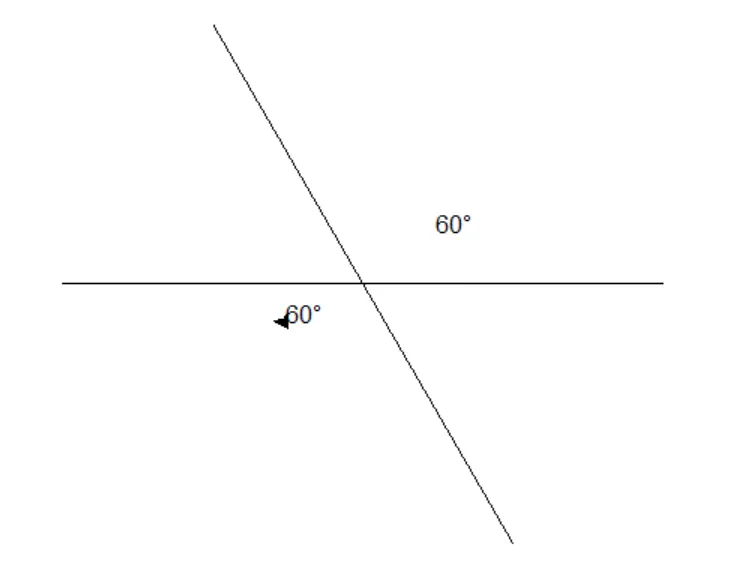
      例如：画轴对称图形、对称轴、对称点坐标。

# 例子1：绘制轴对称花朵（turtle，先画一半，对称画另一半）
import turtle
t = turtle.Turtle()
t.speed(3)

# 绘制花朵的一半（简化版）
t.color("pink")
for _ in range(5):
    t.circle(20, 180)
    t.right(144)

# 移动画笔到对称位置，绘制另一半（以y轴为对称轴）
t.penup()
t.goto(0, 0)
t.setheading(0)
t.pendown()
t.color("pink")
for _ in range(5):
    t.circle(-20, 180)
    t.right(144)

print("已绘制轴对称花朵（以y轴为对称轴）")
turtle.done()

# 例子2：对称点计算（支持y轴、x轴对称）
x = float(input("请输入点的x坐标："))
y = float(input("请输入点的y坐标："))
axis = input("请输入对称轴（x轴/y轴）：")

if axis == "y轴":
    # y轴对称：x变相反数，y不变
    symmetric_x = -x
    symmetric_y = y
    print(f"点({x},{y})关于y轴的对称点坐标为：({symmetric_x},{symmetric_y})")
elif axis == "x轴":
    # x轴对称：y变相反数，x不变
    symmetric_x = x
    symmetric_y = -y
    print(f"点({x},{y})关于x轴的对称点坐标为：({symmetric_x},{symmetric_y})")
else:
    print("暂不支持该对称轴，仅支持x轴和y轴！")

# 例子3：用turtle绘制等腰三角形（带对称轴）
import turtle
t = turtle.Turtle()
t.speed(2)

# 绘制等腰三角形
t.forward(100)
t.left(120)
t.forward(100)
t.left(120)
t.forward(100)

# 绘制对称轴（从顶点到底边中点）
t.penup()
t.goto(50, 0)  # 底边中点
t.pendown()
t.setheading(90)
t.forward(86.6)  # 等腰三角形的高（边长100，高≈86.6）

# 标注对称轴
t.penup()
t.goto(60, 40)
t.pendown()
t.write("对称轴", font=("Arial", 10))

print("已绘制等腰三角形及其中线（对称轴）")
turtle.done()

3. 以“应用题建模”强化数学思维

      将数学应用题转化为编程问题，先分析数学逻辑，再用代码实现，培养“数学建模”能力。

示例1：行程问题中，先明确“路程=速度×时间”的公式，再定义变量v（速度）、t（时间），根据输入的已知条件计算未知量。

4. 以“模拟试验”深化概率认知

       概率学习中手动试验次数有限，用random库模拟大量重复试验（如掷骰子1000次），让学生直观看到“频率趋近于概率”。

5. 循序渐进，贴合七年级认知

      编程内容从“输入输出→变量→条件判断→循环→简单函数”逐步进阶，不讲解复杂语法（如类、装饰器），始终围绕数学知识点展开，避免本末倒置。