本章内容:
1:整除、因数、倍数
2:质数及筛法
3:带余数除法
4:最大公约数
5:格点问题
6:扩展欧几里得算法
7:唯一分解定理
8:求m!的标准质因数分解式
9:同余理论
1:整除、因数、倍数
数论是研究整数基本性质的一门数学。由于数论里有着非常丰富的算法和具体的应用,所以数论也是信息学竞赛中一类重要的题目类型。
小学阶段的数学,很多都是数论的内容。
定义5.1
设a,b是整数,a≠0,如果存在整数q,使得b=aq成立,则称b可被a整除,记作a|b,且称b是a的倍数,a是b的因数(也可称为约数)。
注意:
1)数学上,乘法式子里乘号可以省略,因此aq表示ax*q。
2)定义里并没有要求q≠0,因此,当b=0时,b=a*0总是成立的。因此,0能被任何非零整数a整除,也可以说,0是任何非零整数的倍数(即0倍)。
3)在数学和程序里,都不允许除数a为0。
定理(英语:Theorem)是经过受逻辑限制的证明为真的陈述。
定理5.1 整除的性质
(1)a|b且b|c => a|c。例如,3|6且6|18,则有3|18。"=>"表示"能推出"。
(2)a|b且a|c <=> 对任意的整数x和y,有a|(bx+cy)。"<=>"表示"等价于"。
一般地,a|b₁,...,a|bₖ同时成立 <=> 对任意的整数x₁,...,xₖ,有a |(b₁x₁+...+bₖxₖ)。
(3)设m≠0,那么,a|b <=> ma|mb。
定义5.2
设b是整数,显然,±1,±b一定是b的约数,它们称为b的显然约数;b的其他约数(如果有的话)称为是b的非显然约数,或真因数。
定理5.2
设整数b≠0,d₁,d₂,...,dₖ是它的全体约数。
那么,b/d₁,b/d₂,...,b/dₖ也是它的全体约数。
也就是说,当d遍历完b的全体约数时,b/d也遍历完b的全体约数。
此外,若b>0,当d遍历完b的全体正约数时,b/d也遍历完b的全体正约数
以b=24为例
因为1,2,3,4,6,8,12,24是b的全体正约数。
所以24,12,8,6,4,3,2,1也是b的全体正约数。
推论
平方数的正约数的个数一定是奇数,非平方数的正约数的个数一定是偶数。
2:质数及筛法
定义5.3
设整数p≠0,p≠±1。如果除了显然约数±1,±p外,p没有其他的约数,那么,p就称为质数(或素数)。若整数a±0,a±1,且a不是质数,则a称为合数。注意,0、±1既不是质数也不是合数。
定理5.3
若a是合数,则必有质数p,使得p|a。合数a的最小非显然约数必为质数。
定义5.4
一个整数的因数如果是质数,则这个因数称为该整数的质因数(或素因数)。
定理5.4
设整数a>=2,若a是合数,则必有质数p,使得p|a,p<=√a。
3:带余数除法
定理5.5(带余数除法)
设a与b是两个给定的整数,a≠0。那么一定存在唯一的一对整数q和r,使得:b=qa+r,0<=r<|a|。此外,a|b的充要条件是r=0。
b是被除数,a是除数,所以要求a≠0,我们可以写出带余数除法算式:b÷a=q...r。
还可以写成以下式子 b-a=a*q。
定理5.6
设a与b是两个给定的整数,a≠0,再设d是一个给定的整数,那么一定存在唯一的一对整数q₁和r₁,使得:b=q₁a+r₁,d<=r₁<|a|+d。 此外,a|b的充要条件是a|r₁。
定理5.7
设整数a>0。任一正整数b被a除后所得的最小非负余数是且仅是0,1,...,a-1这a个数中的一个。
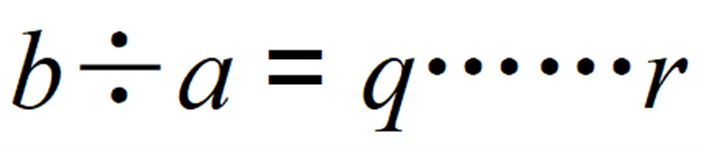
为方便讨论,作出以下约定。
(1)0<=余数r<a。哪怕r=0,也要写出这个余数。r=0,意味着b能被a整除。
(2)b,a,q,r都是(非负)整数,除数a可以大于被除数b,但商q一定小于等于被除数b,余数r也一定小于等于被除数b。
(3)商q可以取0,但除数a不能取0。在数学上和计算机里,除数a都是不能为0的。
(4)在数学上,如果除数a是已知的,题目一般会保证a≠0;如果除数a是未知的,是求出来的,解题时要保证a≠0。
(5)在编程解题时,如果a是输入数据,输入数据也应该视为是已知的;如果没有保证没有保证a≠0,程序要判断;如果a是求出来的,程序要保证a≠0。
在公式中,总共有四个量:被除数b、除数a、商q、余数r。
如果每个量,可能已知、也可能未知,那就总共有2⁴=16种组合。
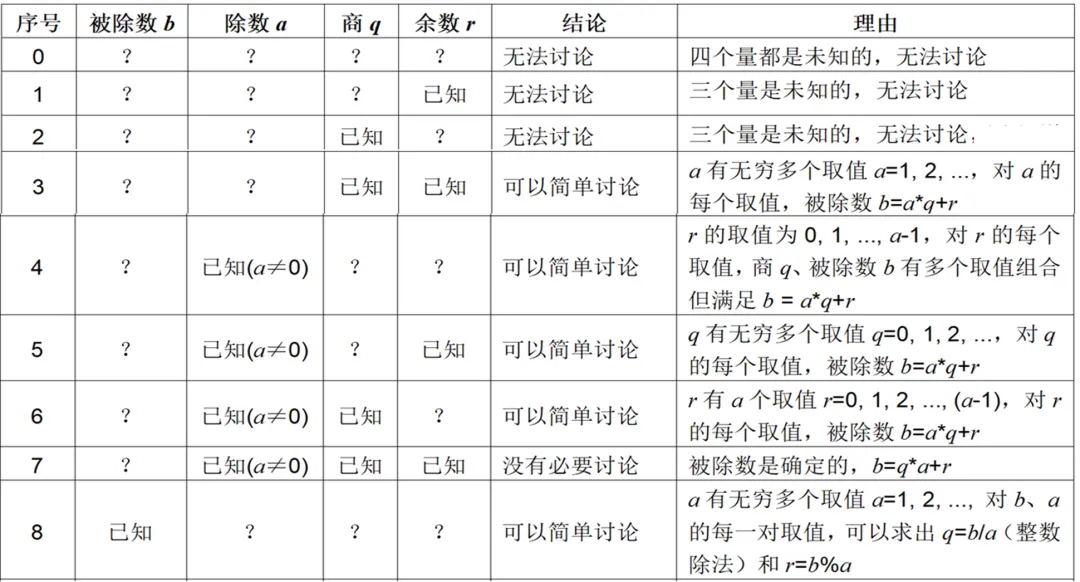
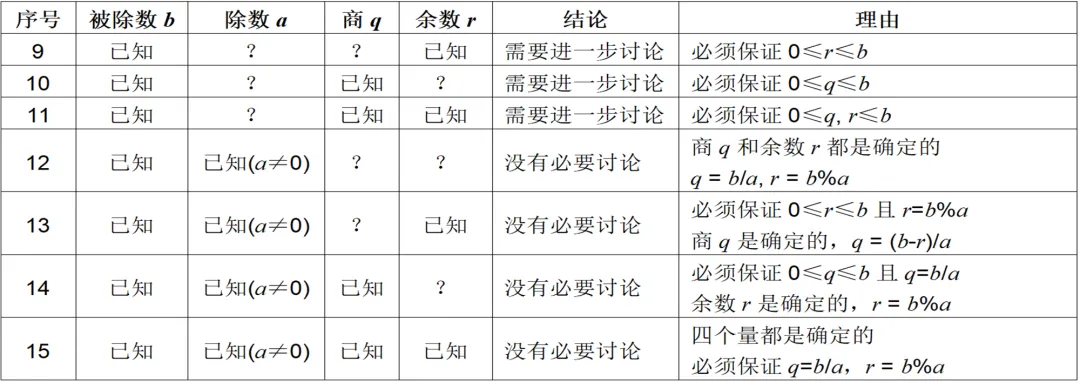
4:最大公约数
定义5.5
设 a₁,a2 是两个整数,如果 d|a₁ 且 d|a₂, 那么,d 就称为是a₁和a₂的公约数
一般地,设 a₁ ,a₂,...,aₖ 是 k 个整数,如果 d|a₁,...,d|aₖ,
那么,d 就称为是 a₁,a₂,...,aₖ 的公约数。
定义5.6
设 a₁,a₂ 是两个不全为零的整数,
把 a₁ 和 a₂ 的公约数中最大的整数称为 a₁ 和 a₂ 的最大公约数。
一般地,设 a₁,a₂,...,aₖ 是 k 个不全为零的整数,
把 a₁,a₂, ....aₖ 的公约数中最大的整数称为 a₁,a₂,...,aₖ的最大太公约数
定义5.7
若 (a₁,a₂)=1, 则称 a₁ 和 a₂ 是互质的。
一般地,若 (a₁,...,aₖ)=1, 则称 a₁,...,aₖ 是互质的。
定理5.8
如果存在整数 x₁ ,.......xₖ,
使得 ai₁x₁+...+aₖxₖ=1, 则 a₁,...,aₖ 是互质的。
定义5.8
设a₁,a₂是两个均不等于零的整数,如果a₁|L且a₂|L,则称L是a₁和a₂的公倍数。
一般地,设a₁,...,aₖ是k个均不等于零的整数,如果a₁|L,...,aₖ|L,则称L是ai,...aₖ的公倍数。
定义5.9
设a₁,a₂是两个均不等于零的整数,把a₁和a2₂的正的公倍数中最小的整数称为a₁和a₂的最小公倍数。
一般地,设a₁,...,aₖ是k个均不等于零的整数,把a₁,...,aₖ的正的公倍数中最小的整数称为a₁,...,aₖ的最小公倍数。
定理5.9(辗转相除法)
设u₀,u₁是给定的两个整数,u₁≠0,(u₀,u₁)=1,则一定可以重复应用带余数除法得到下面k+1个等式:
以上算法就称为辗转相除法或Euclid(欧几里德)算法。
辗转相除法就是反复将较大的数表示成"较小的数的若干倍+余数",直至余数为0,此时较小的数就是最大公约数。
定理5.10
多个数的最大公约数,可以通过逐步求两个数的最大公约数来实现。
定理5.11
最大公约数和最小公倍数的联系 a*b=GCD(a,b)*LCM (a, b)。
定理5.12
多个数的最小公倍数也可以通过逐步求两个数的最最小公倍数来实现。
5:格点问题
在直角坐标系中,x坐标和y坐标均为整数的点,称为格点,也称为整点,如图所示。
在网格坐标系中,网格中的方格,行坐标和列坐标也均为整数,因此方格有时也可以视为格点进行处理。
6:扩展欧几里得算法
丢番图方程(Diophantine Equation):有一个或者几个变量的整系数方程,它们的求解仅仅在整数范围内进行。
最后这个限制使得丢番图方程求解与实数范围方程求解有根本的不同。
丢番图方程又名不定方程、整系数多项式方程,是变量仅容许是整数的多项式等式;
裴蜀定理:对于任意正整数a和b,存在整数x和y,使得ax+by=gcd(a,b),即a和b的线性组合的最小正整数是他们的最大公约数。
几何意义:a和b能表示对最小正整数是其最大公约数。
扩展欧几里得算法:求解该等式中x和y的递归方法。
算法执行过程:
设 a 和 b 为两个整数
如果 b 为 0, 则 x=l,y=0 即为所求,且最大公约数为 a;
否则递归地求解 b 和 a% b 的同类问题 (设解为 x₂ 和 y₂),
并且 x=y₂,y=x₂-a/b*y₂ 为所求的解。

7:唯一分解定理
定理5.14(唯一分解定理、算术基本定理)
设整数a≥2,那么a一定可表示为若干个质数的乘积(包括a本身是质数),
即:a=p₁p₂...pₜ,其中pⱼ(1<j<t)是质数,
相同的质数合并,即得:a=p₁ᵃ¹p₂ᵃ²...pₛᵃˢ,称为是a的标准质因数分解式
定理5.15
设a为正整数,τ(a)表示a的所有正除数的个数(包括1和a本身),
τ(a)通常称为a的除数函数。
那么,τ(1)=1,若a>l且有标准质因数分解式,则
τ(a)=(α₁+1)...(αₛ+1)=τ(p₁ᵃ¹)...τ(pₛᵃˢ)。
定理5.16
设a为正整数,σ(a)表示a的所有正除数之和,
σ(a)通常称为a的除数和函数。
那么,σ(1)=1,当a>l且有标准质因数分解式,则
定理5.17
设n为一个给定的正整数,
p是一个给定的质数,
a是pᵃ|n!的最大整数,
因为必有整数k满足,pᵏ <=n<pᵏ +1
对大于k的正整数j,[n/pʲ]为0。
此后,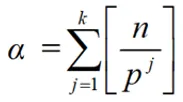
9:同余理论
所谓同余,就是a和b对m取余得到的余数相同。
定义5.10(同余)
设m≠0。若m|(a-b),即a-b=km,可以改写为a-km=b,则称m为模,a同余于b模m,以及b是a对模m的剩余,记作:a=b(mod m)。称为模m的同余式,或简称同余式。
若0<b<m,则称b是a对模m的最小非负剩余;
若1≤b≤m,则称b是a对模m的最小正剩余;
若-m/2<b≤m/2(或-m/2≤b<m/2),则称b是a对模m的绝对最小剩余\
定理5.18
a同余于b模m的充要条件是a和b被m除后所得的最小非负余数相等,即若:
a=q₁m+r₁,0≤r₁<m;
b=q₂m+r₂,0≤r₂<m;
则 r₁=r₂。
定理5.19 同余的性质:
性质Ⅰ:同余是一种等价关系
性质Ⅱ:同余式可以相加
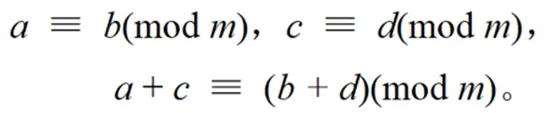
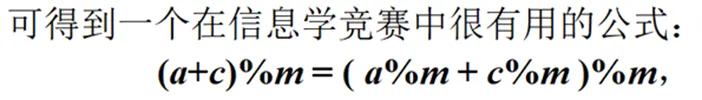
性质Ⅲ:同余式可以相乘
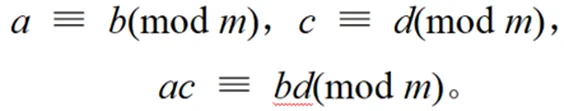
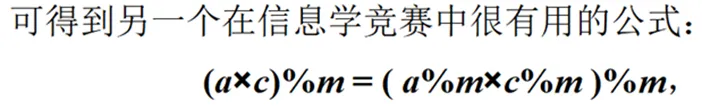
此外,可以在幂云算中运用同余理论
定义5.11(同余类、剩余类)
对给定的模m,整数的同余关系是一个等价关系。全体整数可按对模m是否同余分为若干个两两不相交的集合,使得在同一个集合中的任意两个整数对模m一定同余,而属于不同集合中的两个整数对模m一定不同余。每一个这样的集合称为模m的同余类,或模m的剩余类。用r mod m表示r所属的模m的同余类。
定理5.20
对给定的模m,有且恰有m个不同的模m的同余类,
它们是:0 mod m,1 mod m,....,(m-1)mod m