邹城信奥赛C++编程之基础算法递推和递归

邹城的各位少年你们好,我是生活在邹城市本地的编程万万.这次我们来说一下基础算法中的递推和递归

先看一下递推和递归是什么意思?

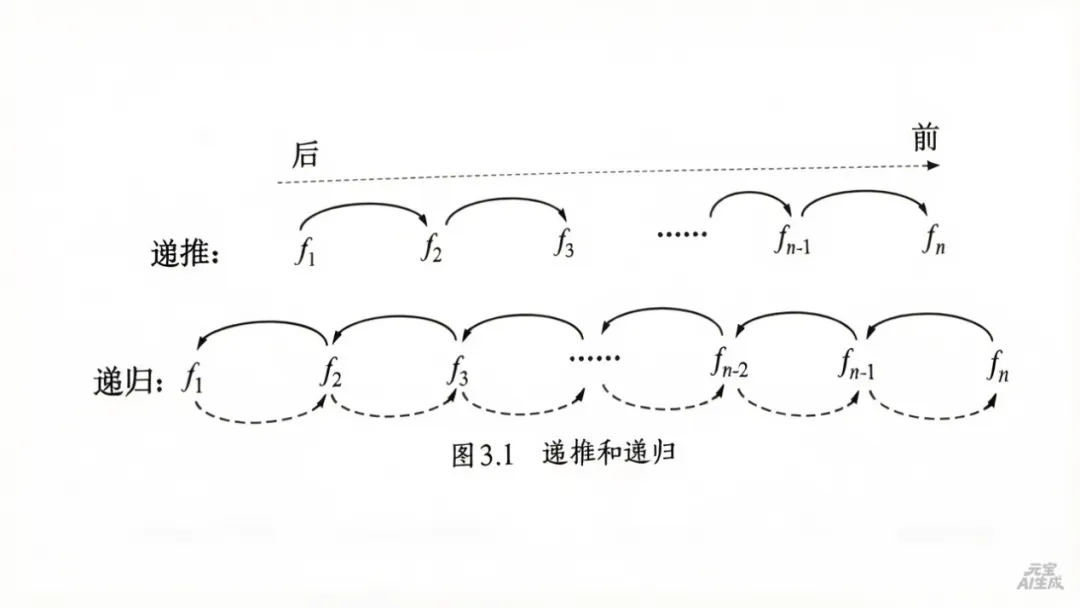
递推,是从已知的初始条件出发,按照递推关系,逐步计算后续各项,直到求的问题的解

递归,是把问题分解为规模更小但形式相同的子问题,通过递归函数调用自身解决,直到到达递归的结束条件

递归要使用递归函数实现,递推不一定使用函数

有些问题,可以找到递推的公式求解

比如经典的斐波那契数列,f1=f2=1,当n>2时,有公示fn=fn-1 +fn-2成立,

要求斐波那契的第n项,有如下两种方法:

(1)递推

可以从f1=f2=1出发,逐次求出f3,f4,f5,...,一直到求出fn

在程序实现时,只需要三个变量f1,f2,f3,表示连续的3项,递推n-2次,就可以求出fn

如果用一个数组,存储数列的每一项的值,会更加直观,也更容易实现

有些问题,不得不用数组存储地推出的每一项.

(2)递归

为了求fn,可以转而去求fn-1和fn-2,去求fn-1,要转而去求fn-2和fn-3

如果有一个函数fun(n),可以求出fn,怎fun(n)要调用fun(n-1)和fun(n-2),因此fuc(n)是一个递归函数

递归函数存在问题,可能会有许多重复的计算

求斐波那契数列的第n项,就有许多重复的计算,根据测算,到求21项时,fun(n)函数的递归调用的次数就高达21891次

如何解决这个问题呢?

(1)定义一个数组f,用来存储求到得每一项

(2)在fun(n)函数中,现去查一下,第n项得值是不是已经在f数组中了,如果已经有,就直接返回结果,没有,再递归求解

(3)接下来得每种情形,都要把求到得解,存储起来