Python绘制主成分分析图(附数据和代码)
- 2026-02-06 19:57:41
Python绘制主成分分析图(附数据和代码)
主成分分析作为经典的多变量数据分析方法,通过正交变换多维复杂指标,降维至少数几个相互独立的主成分维度并实现可视化呈现,借助散点聚类特征、置信椭圆分布及载荷向量指向,可清晰展现管理对象的综合表现差异、群体聚类特征及核心指标的驱动贡献,比较适用于多组学、环境科学、农业或生物医学等领域中对多变量实验数据进行探索性分析。 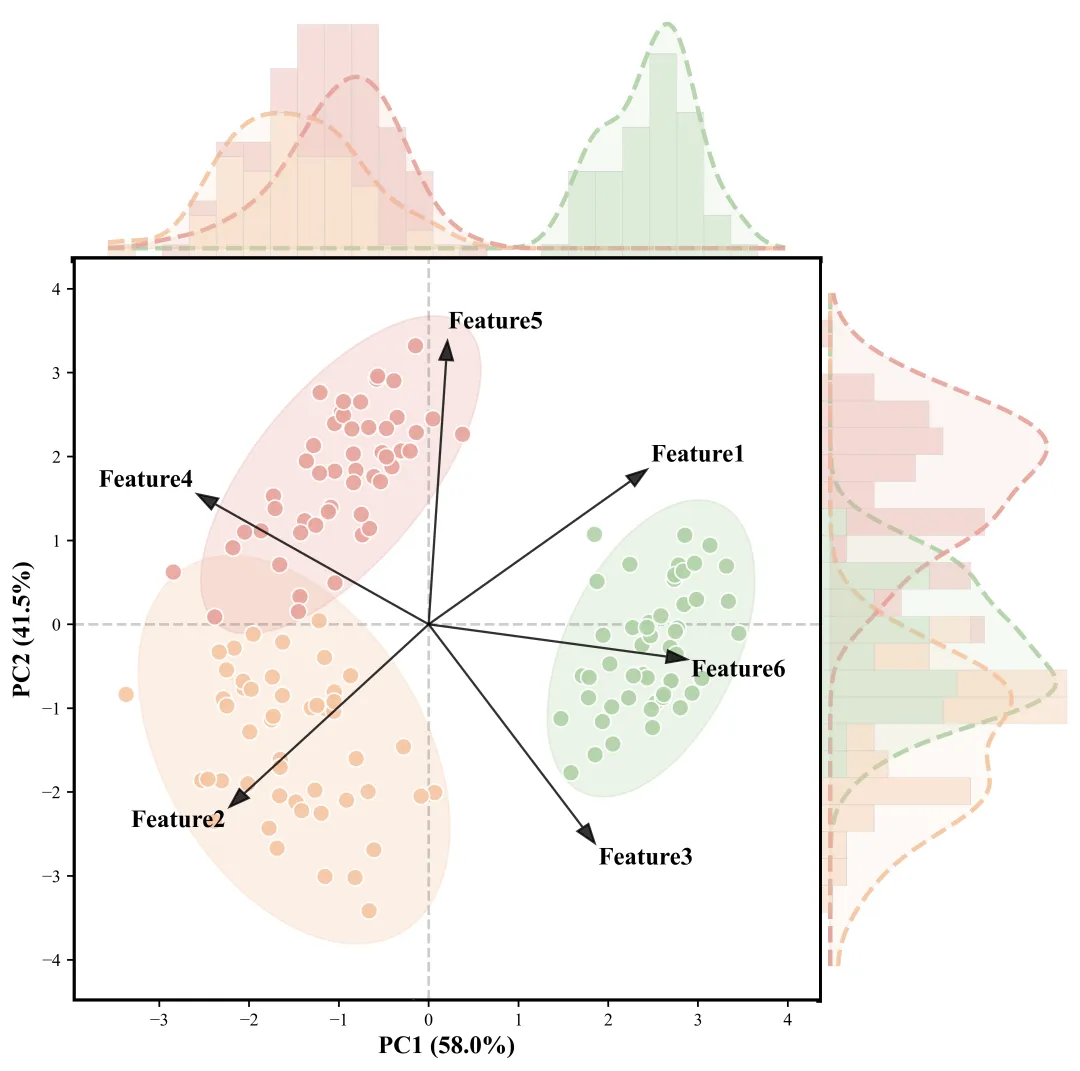




猜您喜欢 往期精选▼
©[悠悠智汇笔记] 版权所有
🙏请尊重劳动成果,守护每一份劳动心血;⚖️未经授权,不得以为任何方式转载、摘编或抄袭。🔄转载合作请后台联系授权,侵权必究。

01

配置全局参数

首先,定义整个流程的常量参数,包括文件路径、随机种子、每组样本数、噪声强度、特征偏移等。特别定义了理论载荷矩阵和三组数据在主成分空间的理想分布。
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.decomposition import PCAfrom sklearn.preprocessing import StandardScalerfrom matplotlib.patches import Ellipsefrom matplotlib.gridspec import GridSpecfrom scipy.stats import gaussian_kde, chi2plt.rcParams['font.family'] = 'Times New Roman'# 文件路径CSV_FILE = "pca_data.csv"OUT_FIG = "pca_plot.png"# 数据生成核心参数RANDOM_SEED = 42N_PER_GROUP = 50NOISE_STD = 0.2# 真实载荷矩阵(核心)TRUE_LOADINGS = np.array([ [-0.9, 0.0], [0.8, 0.1], [0.3, 0.9], [0.1, -0.9], [-0.7, -0.6], [-0.5, 0.7]])# 组配置(核心)GROUP_CONFIGS = { "Group1": {"center": [-3, 3], "scale": [1.2, 0.8]}, "Group2": {"center": [3, -1], "scale": [0.9, 1.5]}, "Group3": {"center": [-1, -4], "scale": [1.5, 0.7]},}# 基础列名与颜色FEATURE_COLS = [f"Feature{i}" for i in range(1, 7)]GROUP_COL = "Group"COLORS = ["#b0d1a6", "#f5c5a0", "#e7a39a"]# 图形核心参数(删减边缘图、箭头等次要参数)FIGSIZE = (10, 10)GS_NROWS, GS_NCOLS = 4, 4SCATTER_S = 90SCATTER_ALPHA = 0.9ELLIPSE_ALPHA = 0.2502

生成模拟数据

导入 PCA 分析和绘图所需的全部库,定义数据生成、图形绘制的核心参数,设定分组、特征、颜色等固定配置,为后续代码提供统一调用标准。
def generate_scattered_data(filename: str = CSV_FILE) -> str: """生成模拟的PCA数据并保存为CSV文件""" np.random.seed(RANDOM_SEED) all_data = [] for group_name, cfg in GROUP_CONFIGS.items(): # 生成主成分得分 s_pc1 = np.random.normal(cfg["center"][0], cfg["scale"][0], N_PER_GROUP) s_pc2 = np.random.normal(cfg["center"][1], cfg["scale"][1], N_PER_GROUP) scores = np.vstack([s_pc1, s_pc2]).T # 生成原始特征数据(删减噪声添加的注释) x_raw = scores @ TRUE_LOADINGS.T + np.random.normal(0, NOISE_STD, (N_PER_GROUP, len(FEATURE_COLS))) df_group = pd.DataFrame(x_raw, columns=FEATURE_COLS) df_group[GROUP_COL] = group_name all_data.append(df_group) df_total = pd.concat(all_data, ignore_index=True) df_total.loc[:, FEATURE_COLS] += 10 # 直接写死偏移量,删减FEATURE_OFFSET参数 df_total.to_csv(filename, index=False) return filename03

边缘图绘制

基于主图坐标范围对齐边缘图尺度,绘制顶部和右侧的分组堆叠直方图展示单主成分分布,添加 KDE 密度曲线强化分布趋势,简化刻度控制保证图形整洁。
def plot_margin_type_5(ax_top, ax_right, group_data_list, ax_main, bins: int = 25): x_min, x_max = ax_main.get_xlim() y_min, y_max = ax_main.get_ylim() x_bins = np.linspace(x_min, x_max, bins + 1) y_bins = np.linspace(y_min, y_max, bins + 1) x_hist_data, y_hist_data = [], [] for _, data, color, _marker in group_data_list: x_counts, _ = np.histogram(data["PC1"], bins=x_bins) y_counts, _ = np.histogram(data["PC2"], bins=y_bins) x_hist_data.append((x_counts, color)) y_hist_data.append((y_counts, color)) x_centers = (x_bins[:-1] + x_bins[1:]) / 2 x_bottom = np.zeros(len(x_centers)) for counts, color in x_hist_data: ax_top.bar(x_centers, counts, width=(x_bins[1] - x_bins[0]), bottom=x_bottom, color=color, alpha=0.35) x_bottom += counts y_centers = (y_bins[:-1] + y_bins[1:]) / 2 y_bottom = np.zeros(len(y_centers)) for counts, color in y_hist_data: ax_right.barh(y_centers, counts, height=(y_bins[1] - y_bins[0]), left=y_bottom, color=color, alpha=0.35) y_bottom += counts ax_dens_x = ax_top.twinx() ax_dens_y = ax_right.twiny() x_plot = np.linspace(x_min, x_max, 200) y_plot = np.linspace(y_min, y_max, 200) for _, data, color, _marker in group_data_list: x_kde = gaussian_kde(data["PC1"]) ax_dens_x.plot(x_plot, x_kde(x_plot), color=color, linewidth=2.5, alpha=0.9) y_kde = gaussian_kde(data["PC2"]) ax_dens_y.plot(y_kde(y_plot), y_plot, color=color, linewidth=2.5, alpha=0.9) ax_top.tick_params(axis="x", bottom=False, labelbottom=False) ax_right.tick_params(axis="y", left=False, labelleft=False) ax_dens_x.tick_params(axis="y", right=False, labelright=False) ax_dens_y.tick_params(axis="x", top=False, labeltop=False)04

核心绘图

定义 95% 置信椭圆函数展示分组数据的分布范围,定义载荷向量函数绘制特征贡献箭头,直观呈现特征对主成分的影响程度。
def add_confidence_ellipse_95(ax, x: np.ndarray, y: np.ndarray, color: str): cov = np.cov(x, y) vals, vecs = np.linalg.eigh(cov) order = vals.argsort()[::-1] vals = vals[order] vecs = vecs[:, order] vx, vy = vecs[:, 0] theta = np.degrees(np.atan2(vy, vx)) scale = np.sqrt(chi2.ppf(0.95, df=2)) width = 2 * scale * np.sqrt(vals[0]) height = 2 * scale * np.sqrt(vals[1]) ax.add_patch(Ellipse(xy=(np.mean(x), np.mean(y)), width=width, height=height, angle=theta, facecolor=color, alpha=ELLIPSE_ALPHA, edgecolor=color, zorder=2))def add_loading_vectors(ax, loadings: np.ndarray): for i, feat in enumerate(FEATURE_COLS): vx, vy = loadings[i, 0] * 5.0, loadings[i, 1] * 5.0 ax.arrow(0, 0, vx, vy, color="black", alpha=0.8, head_width=0.15, lw=1.2) ax.text(vx * 1.1, vy * 1.1, feat, fontsize=14, fontweight="bold")05

PCA 分析与绘图主流程

读取模拟数据并执行 PCA 分析,划分主图与边缘图的网格布局,绘制分组散点图和置信椭圆,添加载荷向量与参考线,调用边缘图函数补充分布特征后保存图形。
csv_file = generate_scattered_data(CSV_FILE)df = pd.read_csv(csv_file)X_scaled = StandardScaler().fit_transform(df[FEATURE_COLS])pca = PCA(n_components=2)pca_res = pca.fit_transform(X_scaled)loadings = pca.components_.Tpca_df = pd.DataFrame({"PC1": pca_res[:, 0], "PC2": pca_res[:, 1], GROUP_COL: df[GROUP_COL]})fig = plt.figure(figsize=FIGSIZE)gs = GridSpec(GS_NROWS, GS_NCOLS, hspace=0.0, wspace=0.0)ax_main = fig.add_subplot(gs[1:4, 0:3])ax_top = fig.add_subplot(gs[0, 0:3], sharex=ax_main)ax_right = fig.add_subplot(gs[1:4, 3], sharey=ax_main)groups = df[GROUP_COL].unique()plot_data_for_margin = []for i, group in enumerate(groups): data = pca_df[pca_df[GROUP_COL] == group] color = COLORS[i % len(COLORS)] plot_data_for_margin.append((group, data, color, "o")) ax_main.scatter(data["PC1"], data["PC2"], c=color, s=SCATTER_S, alpha=SCATTER_ALPHA, edgecolors="white") add_confidence_ellipse_95(ax_main, data["PC1"].to_numpy(), data["PC2"].to_numpy(), color) add_loading_vectors(ax_main, loadings) ax_main.axhline(0, color="gray", ls="--", alpha=0.4) ax_main.axvline(0, color="gray", ls="--", alpha=0.4) plot_margin_type_5(ax_top, ax_right, plot_data_for_margin, ax_main) plt.savefig(OUT_FIG, dpi=600, bbox_inches="tight")🌿 今日的分享就到这里啦~如果这些内容有为你带来帮助,欢迎轻点右下角的【👍赞】和【👀在看】,也欢迎分享给更多需要的人,感恩~
THE
END


数据和代码怎么获取?
点击关注后,后台回复关键词:
2026_map_008可直接获取完整的示例数据和代码
如有帮助,您的点赞、评论、转发是我持续创作的动力~


本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。