【少儿编程】|《数字黑洞153》源程序
- 2026-01-22 12:37:36
WELCOME TO
少儿编程,编程向未来
Scratch
数
字
黑
洞
153

数字黑洞 153:三位数的 “水仙花数黑洞”
153 是一个极具特色的数字黑洞,专门针对各位数字之和能被 3 整除的三位数(也可延伸到更多位数)—— 任意符合条件的数,按 “拆分数字→立方求和→重复运算” 的规则迭代,最终一定会收敛到 153,且一旦落入 153 就不再变化(153 自身满足 “各位数字立方和 = 自身”)。它既是 “水仙花数”(三位自幂数),也是数论中 “自幂数黑洞” 的典型代表。
核心规则:简单两步,锁定黑洞
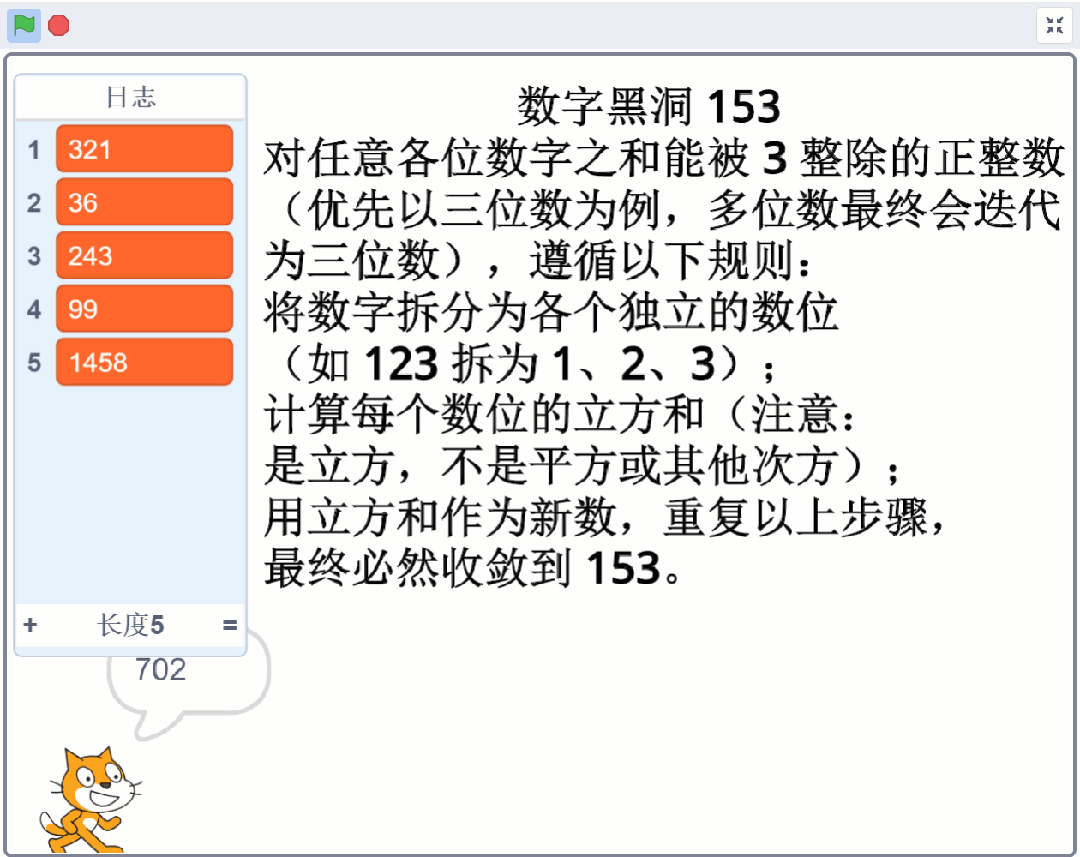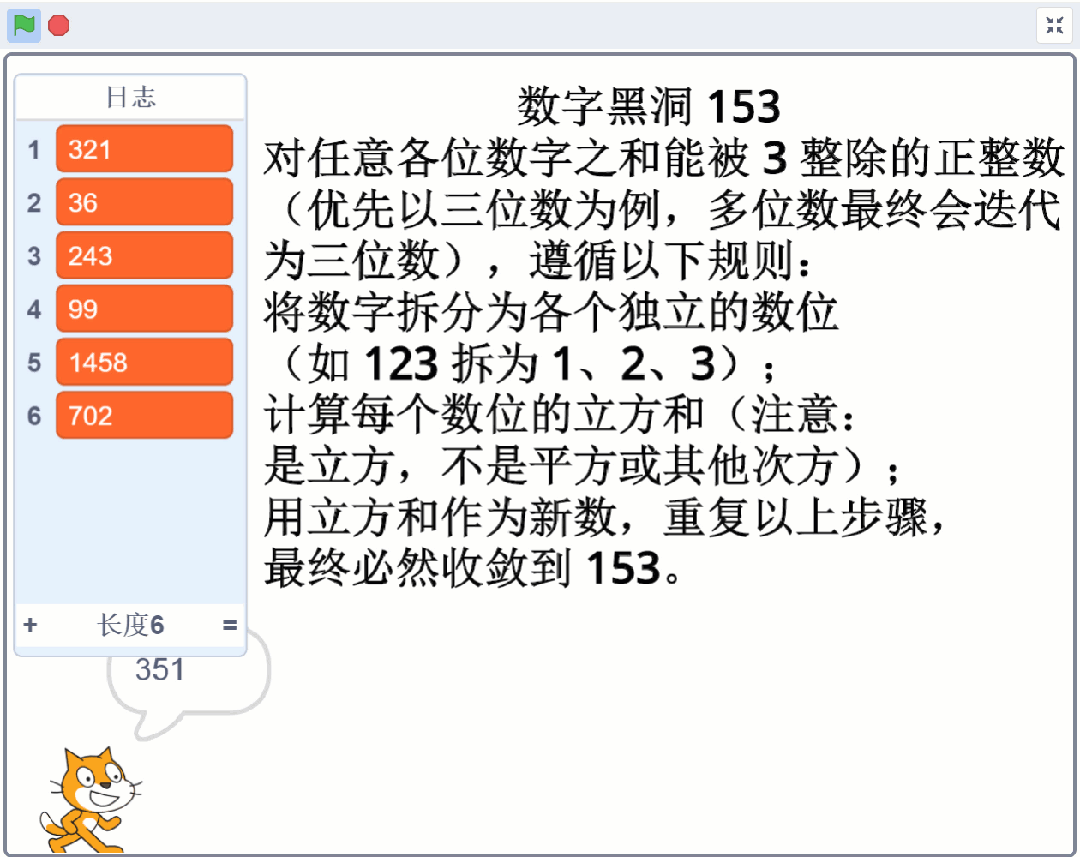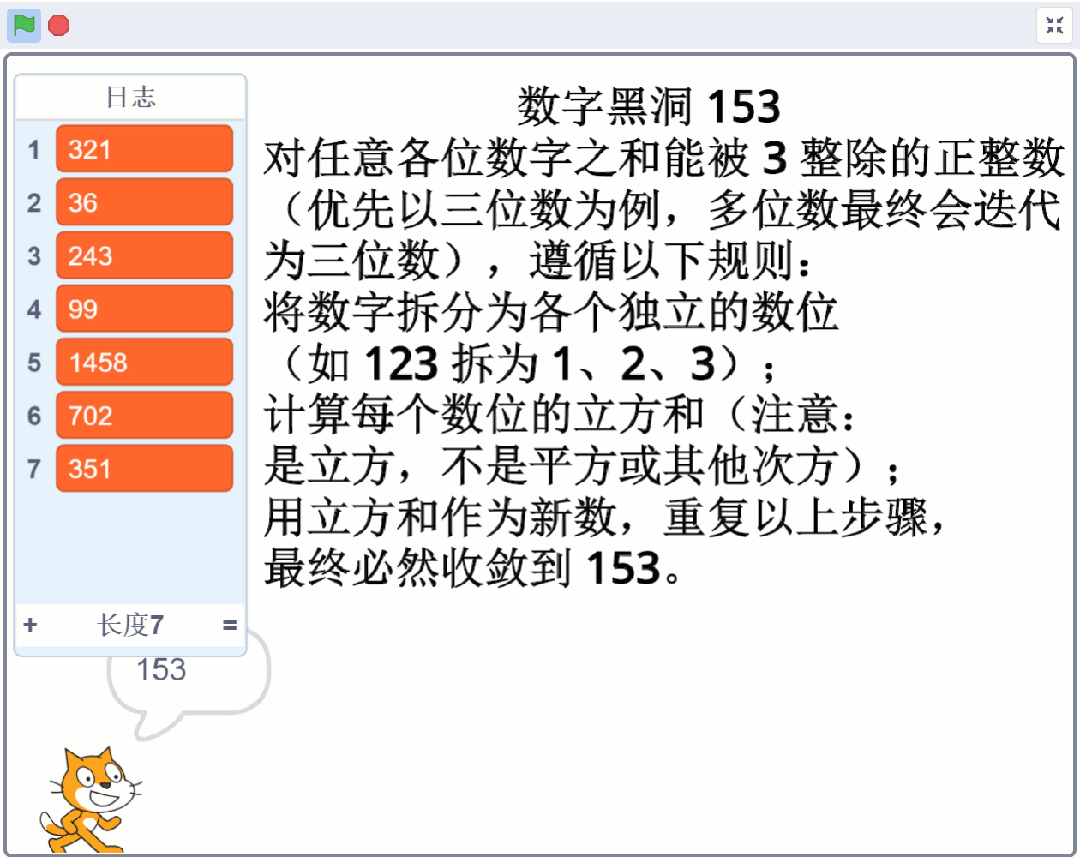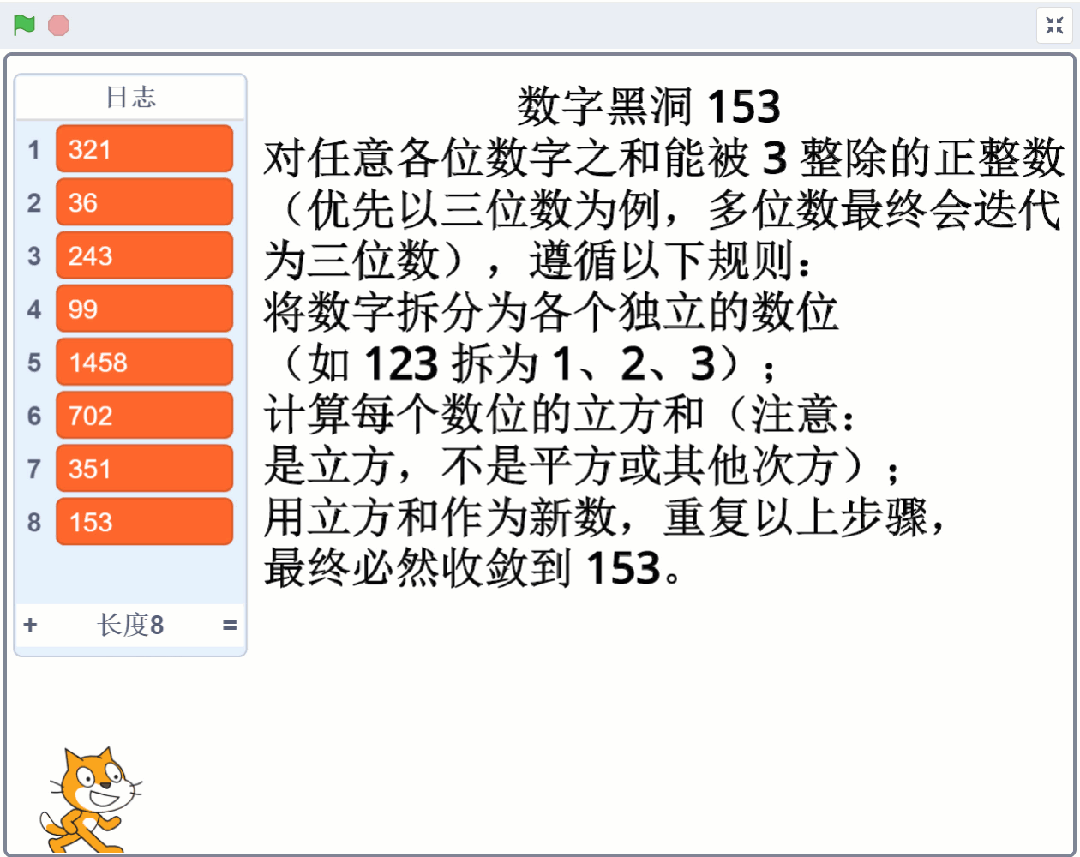
对任意各位数字之和能被 3 整除的正整数(优先以三位数为例,多位数最终会迭代为三位数),遵循以下规则:
将数字拆分为各个独立的数位(如 123 拆为 1、2、3);
计算每个数位的立方和(注意:是立方,不是平方或其他次方);
用立方和作为新数,重复以上步骤,最终必然收敛到 153。
关键前提:为什么要求 “各位数字之和能被 3 整除”?
因为一个数能被 3 整除,是它的各位数字立方和也能被 3 整除的充要条件(数论定理)。153 本身能被 3 整除(1+5+3=9),只有初始数满足 “能被 3 整除”,迭代过程中所有新数才会持续能被 3 整除,最终才能收敛到 153;若初始数不能被 3 整除,会落入其他循环(如 407→4³+0³+7³=64+0+343=407,形成独立循环),无法进入 153 黑洞。
案例 :三位数入门 —— 以 “123” 为例(1+2+3=6,能被 3 整除)
123 → 1³ + 2³ + 3³ = 1 + 8 + 27 = 3636 → 3³ + 6³ = 27 + 216 = 243243 → 2³ + 4³ + 3³ = 8 + 64 + 27 = 9999 → 9³ + 9³ = 729 + 729 = 1458(多位数自动拆分为 1、4、5、8)1458 → 1³ + 4³ + 5³ + 8³ = 1 + 64 + 125 + 512 = 702702 → 7³ + 0³ + 2³ = 343 + 0 + 8 = 351351 → 3³ + 5³ + 1³ = 27 + 125 + 1 = 153(进入黑洞)153 → 1³ + 5³ + 3³ = 1 + 125 + 27 = 153(稳定不变)。
153 之所以能成为 “黑洞核心”,关键在于它是三位水仙花数(自幂数的一种)—— 即 “一个 n 位数,其各位数字的 n 次方和等于它本身”:
153 是 3 位数,各位数字的 3 次方和 = 1³+5³+3³=1+125+27=153,完美满足自幂数定义;
自幂数本身是 “迭代不动点”:一旦迭代到自幂数,后续运算结果永远是它自己,因此自然成为黑洞的 “终点”。
听说还有:4 位水仙花数黑洞 8128”(4 位数按 “4 次方和” 迭代收敛到 8128),你想验证一下吗?
往
期推荐

温馨提示:点击阅读原文即可查看百度网盘链接,查看《数字黑洞153》源程序。打开Scratch3.0软件,上传即可运行。有疑问可在后台留言,也可+V,谢谢您的关注!一起成为很哇塞的人!
回复“编程源码库”,查看更多编程源码!

