考级｜2025年12月 GESP六级编程题解析

1. [GESP202512八级] 猫和老鼠

推出结论后直接套用最短路dijkstra模板即可。

考点：最短路算法

题目练习链接：https://xsdoi.com/problem/GESP8017

1.1. 题面

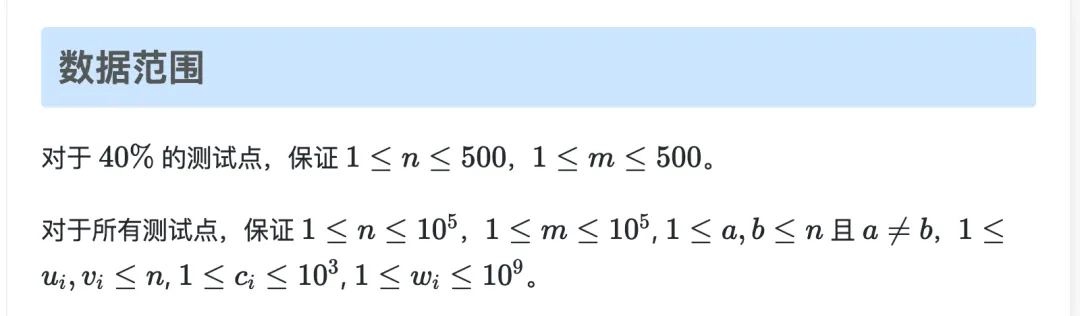
1.2. 题意

给定  个点 和  条边的连通带权无向图，边权为通过该边所需时间，猫在 ，鼠洞在 ，每个点有奶酪价值 。

•  是安全点：当且仅当存在  的路径，路径上任意点 ，猫从  到  的最短时间 > 老鼠从  到  的最短时间。

求所有安全点的奶酪价值总和。

1.3. 题解

暴力做一遍全源最短路肯定不可能，所以我们考虑转化问题。

如果猫能在某个节点抓住老鼠，那么他在这个节点赶到鼠窝在抓也是一样的。

所以说一个节点是安全的当且仅当猫不能在老鼠之前赶到鼠窝。

那么做法就很显然了：在鼠窝跑一遍最短路，对每个节点判一遍，统计所有距离小于鼠窝至猫窝距离的答案。

1.4. 代码

#include<bits/stdc++.h>#define pi pair<ll, ll>usingnamespacestd;typedeflonglong ll;const ll N = 100005;ll n, m, c[N], d[N], vis[N], a, b, ans = 0;vector<pi> e[N];priority_queue<pi, vector<pi>, greater<pi> > q;intmain(){cin >> n >> m;cin >> a >> b;for (int i = 1; i <= n; i++) cin >> c[i];for (int i = 1; i <= m; i++) {        ll u, v, w;cin >> u >> v >> w;        e[u].push_back({v, w});        e[v].push_back({u, w});    }for (int i = 1; i <= n; i++) d[i] = 1e18;    d[b] = 0;    q.push({0, b});while (!q.empty()) {        ll u = q.top().second;        q.pop();if (vis[u]) continue;        vis[u] = 1;for (auto p : e[u]) {            ll v = p.first, w = p.second;if (d[v] > d[u] + w) {                d[v] = d[u] + w;                q.push({d[v], v});            }        }    }for (int i = 1; i <= n; i++) {if (d[i] < d[a]) ans += c[i];    }cout << ans << endl;return0;}

2. [GESP202512八级] 宝石项链

本题倍增套路与 [GESP202403 八级] 接竹竿如出一辙，可以对照解题思路理解倍增思想。

考点：动态规划、倍增

题目练习链接：https://xsdoi.com/problem/GESP8018

2.1. 题面

2.2. 题意

一个环形项链，将其划分成尽量多的段，使得每一段中包含了所有种类的宝石，求最多的段数。

2.3. 题解

先将环形线性化，将环形数组复制一遍形成一个长度为  的线性数组 ，这样任意位置  向右寻找最短合法段都可以在这条直线上找到。

用双指针在数组  上遍历，预处理出数组 ，其中  的含义为从位置  开始，最短覆盖所有宝石种类的右区间坐标，使用一个  数组作为桶数组记录每个种类的宝石出现了多少次，用  变量记录一共有多少个不同的宝石种类。

接着就可以模拟划分过程了，我们可以使用倍增来快速求解，数组  表示从第  个宝石向后划分  个区间最短覆盖到的宝石坐标。

最后枚举每个起点，因为我们跳的长度不能超过 n。从高位向低位尝试跳跃，若跳跃仍在上限之内就继续跳，累计跳过的段数即该起点能划分的段数，取所有起点的最大值即为最终答案。

2.4. 代码

#include<bits/stdc++.h>usingnamespacestd;constint N = 2e5 + 5;int n, m, t[N], cnt[N], jump[20][N];int ans = 0, tot = 0;intgo(int u){int sum = 0, res = 0;for (int i = 20 - 1; i >= 0; i--) {if (sum + jump[i][u] <= n) {            sum += jump[i][u];            res += 1 << i;            u = (u + jump[i][u] - 1) % n + 1;        }    }return res;}intmain(){scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {scanf("%d", &t[i]);        t[i + n] = t[i];    }for (int i = 1, r = 0; i <= n; i++) {while (tot < m) {            r++;if (!cnt[t[r]]++) tot++;        }        jump[0][i] = r - i + 1;if (!--cnt[t[i]]) tot--;    }for (int i = 1; i < 20; i++) {for (int j = 1; j <= n; j++) {int tar = (j + jump[i - 1][j] - 1) % n + 1;            jump[i][j] = min(jump[i - 1][j] + jump[i - 1][tar], 1000000000);        }    }for (int i = 1; i <= n; i++) ans = max(ans, go(i));printf("%d\n", ans);return0;}