新年将至,少不了年会,以及年会上的抽奖。本年经过2次年会号码抽奖后,有人问我,有没有办法知道下次的中奖号码;
有的有的,自然是有的。来看看:通过已抽奖的结果,来预测接下来的中奖号码。
1.数据预测的原则
数据预测,主要以已有数据结果,选择合适模型建模,再使用模型预测;
一般会把数据结果划分为训练集和测试集(如8:2),使用模型(如向量机\贝叶斯\随机森林...)来训练模型;用测试集验证。
2. 号码抽奖的逻辑思考
2.1 数据来源
需要有历史抽奖结果的号码数据;来训练模型;
今年已有两次年会抽奖,这两次中奖号码结果,可以作为分析输入。
当然,数据预测2组数据太少,预测稳定性差。可行办法还有:
下次年会开始前,自己偷摸提前半小时达到,自己先模拟个几十组抽奖;记录每组中奖号码结果;来作为训练集。
2.2 预测参数
这里有几个变量参数需要考虑:
1)每次年会总人数n不定;即抽奖号码总数不定;
2)奖项我们一直是4-3-2-1-特等奖,所以种类先固定为5类; 但是每一类的中奖数量也不一样;同样是变量参数;
2.3 抽奖方式
每人先选择一个号码,抽奖抽到对应号码即中奖。
1)无放回抽奖:号码已中奖后,会扔出抽奖奖池。
2)抽奖顺序:按照4-3-2-1-特等奖的顺序抽奖,不是一次抽取;
那4等奖的抽奖结果,会影响3-2-1-特等奖的概率;依次;3等奖结果,影响2-1-特等奖的概率......
3. 通过python实现数据预测
3.1 模型选择
该方式的模型有很多;最简单的直接random;但基于历史数据的参考;最后选择蒙特卡罗模型。
蒙特卡罗模型,也是一种随机抽样的方法;依赖概率理论,通过随机实验近似求解问题;不再详细解读。
3.2 历史数据导入
总号码数、奖品等级数量 都是不确定的,所以在训练数据时,最好先将历史结果,以变量的方式导入模型;
def __init__(self): self.history = [] #先创建列表,值为字典;存储历史的结果数据,即训练数据 self.alpha = alpha # 先验参数,后面的贝叶斯中需使用#total:总的抽奖号码数 ; his_data:历史抽奖结果,是个字典;奖次:中奖号码def add_history(self, total, his_data): # 先验证下传入的历史数据是不是是无放回的 all_numbers = [] for prize, nums in his_data.items(): all_numbers.extend(nums) if len(all_numbers) != len(set(all_numbers)): # all_numbers如果有重复号码,两者会长度会不一样 print("传入的训练数据,号码重复了") self.history.append({ 'total': total,#号码总数 'his_data': his_data,#历史中奖奖项及对应号码结果 'all_numbers': all_numbers #所有的中奖号码 })# 记录历史数据3.3
3.3 利用历史抽奖结果,使用贝叶斯方法计算每个号码的后验概率
根据历史抽奖已知的结果,来影响随机抽奖预测的结果;
最简单的方式:就是根据历史抽奖号码出现的频率,给号码加权重;但是有个问题,历史数据太少,且历史数据号码数量也不一样;
所以这里还是引用更精确的贝叶斯理论(具体原理不再阐述)
贝叶斯理论:通过先验概率与观测数据结合,利用贝叶斯公式计算后验概率,以最小化分类错误率为准则进行最优决策;
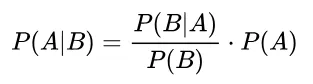
#使用贝叶斯方法计算每个号码的后验概率 #返回:字典,键为号码,值为后验概率def _calculate_bayesian_probabilities(self, total_people): if not self.history: # 如果没有历史数据,返回均匀分布 uniform_prob = 1.0 / total_people return {num: uniform_prob for num in range(1, total_people + 1)} history_counts = {}# 计算每个号码在历史中出现的次数 total_draws = len(self.history) for record in self.history: for num in record['all_numbers']: history_counts[num] = history_counts.get(num, 0) + 1 history_freq = {}# 计算每个号码的历史频率 for num in range(1, total_people + 1): count = history_counts.get(num, 0) history_freq[num] = (count + 1) / (total_draws + total_people)# 避免概率为0 prior_prob = 1.0 / total_people#设置先验分布(均匀分布) bayesian_probs = {}#贝叶斯:后验 ∝ 先验 × 似然 for num in range(1, total_people + 1):# 结合先验和似然 prior_weight = self.alpha #加权平均,alpha控制先验权重 likelihood_weight = 1.0 bayesian_prob = ( prior_weight * prior_prob + likelihood_weight * history_freq[num]) / (prior_weight + likelihood_weight) bayesian_probs[num] = bayesian_prob total_prob = sum(bayesian_probs.values()) # 确保概率之和为1 for num in bayesian_probs: bayesian_probs[num] /= total_prob return bayesian_probs
3.3 使用贝叶斯概率进行蒙特卡洛模拟预测
现在使用蒙特卡洛模型,来模拟年会实际的抽奖逻辑,来进行训练;
#total_peopl总号码数;prize_counts:下次抽奖的奖项及数量;simulations:模拟随机抽奖的次数 def monte_carlo_bayesian_predict(self, total_people, prize_counts, simulations=5000): draw_order = ['四等奖', '三等奖', '二等奖', '一等奖', '特等奖'] # 定义抽奖顺序(从低等奖到特等奖) bayesian_probs = self._calculate_bayesian_probabilities(total_people) # 计算贝叶斯后验概率 print(f"最高概率的5个号码: {sorted(bayesian_probs.items(), key=lambda x: x[1], reverse=True)[:5]}") number_counts = {i: 0 for i in range(1, total_people + 1)}# 记录每个号码抽中的次数 for sim in range(simulations):# 进行多次模拟 available = list(range(1, total_people + 1))# 每次模拟都进行一次完整的抽奖 for prize in draw_order: # 按顺序抽取每个奖项 if prize in prize_counts: need = prize_counts[prize] # 需要抽取的数量 if len(available) < need:# 如果号码不够,跳出 防止奖数比人数还多的bug break # 使用基于贝叶斯概率的随机选择 available_copy = available.copy()#副本,避免影响原来的值 chosen = self._bayesian_sample_without_replacement( available_copy, need, bayesian_probs) for num in chosen:# 记录结果 number_counts[num] += 1 for num in chosen: # 不放回抽奖,从可用号码中移除已选择的号码 available.remove(num) return self._make_prediction(number_counts, total_people, prize_counts)# 根据模拟结果生成预测
根据历史抽奖结果,使用贝叶斯公式,计算后验概率;再蒙特卡洛模拟随机抽奖
#基于贝叶斯概率的不放回抽样#available: 可用号码列表;need: 需要抽取的数量;bayesian_probs: 贝叶斯概率字典def _bayesian_sample_without_replacement(self, available, need, bayesian_probs): chosen = [] # 不放回抽样 for _ in range(need): if not available: break total_prob = sum(bayesian_probs[num] for num in available)#计算当前可用号码的概率 r = random.random() * total_prob# 生成随机数并选择号码 cumulative = 0 selected_num = None for num in available: cumulative += bayesian_probs[num] if r <= cumulative: selected_num = num break chosen.append(selected_num) # 添加选中的号码 available.remove(selected_num)# 从可用列表中移除 return chosen
放回抽奖;记录抽奖的结果。
3.4 根据上面的模拟抽奖结果,来进行预测
#number_counts: 每个号码抽中的次数 total_people: 总人数;prize_counts: 下次抽奖各奖项数量def _make_prediction(self, number_counts, total_people, prize_counts): sorted_numbers = sorted(number_counts.items(), key=lambda x: x[1], reverse=True)# 按被抽中次数从高到低排序 draw_order = ['五等奖', '四等奖', '三等奖', '二等奖', '一等奖'] # 抽奖顺序(从低等到高等) prediction = {} # 存储预测结果 used_numbers = set() # 已使用的号码 for prize in draw_order: # 按顺序分配号码给各个奖项 if prize in prize_counts: need = prize_counts[prize]# 需要抽取的数量 chosen = [] # 选择的号码 for num, count in sorted_numbers:# 从未使用的号码中,按模拟出现次数从高到低选择 if num not in used_numbers and len(chosen) < need: chosen.append(num) used_numbers.add(num) if len(chosen) < need: # 如果还不够,从未使用的号码中随机选择 remaining = [n for n in range(1, total_people + 1) if n not in used_numbers] extra = random.sample(remaining, need - len(chosen)) chosen.extend(extra) used_numbers.update(extra) prediction[prize] = sorted(chosen) # 记录预测结果 return prediction
把上一步模拟抽奖的结果,包括模拟抽奖的号码、次数等,传入_make_prediction;来进行最终的预测。
3.4 主函数,传入历史抽奖的结果,和下次抽奖的号码数、奖项及对应的数量
1)历史中奖数据
前两次年会中奖号码以及记不住了,也以防后面抽奖,有同事直接套用案例的号码结果;我们就随便写一些中奖号码情况;
案例的前两次实际中奖号码结果:
3)完成主函数的数据输入
#主函数,将以上函数需要的数据输入,并进行贝叶斯理论的蒙特卡洛预测def main(): alphas = [0.5, 1.0, 2.0] # 不同的alpha先验强度,影响贝叶斯后验概率 for alpha in alphas: print(f"\n{'='*50}") print(f"使用先验参数 alpha = {alpha}") predictor = BayesianLotteryPredictor(alpha=alpha)# 创建预测器,BayesianLotteryPredictor为以上函数的总类class results1 = { # 第一次年会抽奖结果 '四等奖': [17, 7, 18, 28, 33,24,9], # 第一次年会四等奖号码7个 '三等奖': [5, 12, 25, 35,8], # 第一次年会三等奖号码5个 '二等奖': [3, 17, 30], # 第一次年会二等奖号码3个 '一等奖': [18, 22], # 第一次年会一等奖号码2个 '特等奖': [11] # 第一次年会特等奖号码1个 } predictor.add_history(37, results1)#第一次总抽奖人数37人 results2 = { # 第二次年会抽奖结果 '四等奖': [4, 11, 20, 29, 34,42,22,18,52,9], # 第2次年会四等奖号码10个 '三等奖': [2, 14, 27, 36,43,28], # 第2次年会三等奖号码6个 '二等奖': [8, 24, 31,19,32], # 第2次年会二等奖号码5个 '一等奖': [5, 19,47], # 第2次年会一等奖号码3个 '特等奖': [12] # 第2次年会特等奖号码1个 } predictor.add_history(56, results2)#第2次总抽奖人数56人 # 设置第三次抽奖的参数 print("\n=== 第三次抽奖预测 ===") total_people = 35 #下次抽奖总人数 prize_counts = { '四等奖': 6, #下次抽奖四等奖6个 '三等奖': 4, #下次抽奖三等奖4个 '二等奖': 3, #下次抽奖二等奖3个 '一等奖': 2, #下次抽奖一等奖2个 '特等奖': 1 #下次抽奖特等奖1个 } print("\n贝叶斯蒙特卡洛预测结果:") prediction = predictor.monte_carlo_bayesian_predict( total_people, prize_counts, simulations=3000 ) # 使用贝叶斯蒙特卡洛模拟预测 # 按4-特等奖抽奖顺序显示结果 for prize in ['四等奖', '三等奖', '二等奖', '一等奖', '特等奖']: if prize in prediction: print(f" {prize}: {prediction[prize]}")
4)查看预测结果
if __name__ == "__main__": main()
贝叶斯的蒙特卡洛预测结果: alpha = 0.5
一等奖29,32号;特等奖3号
贝叶斯的蒙特卡洛预测结果: alpha = 1
一等奖30,33号;特等奖4号
贝叶斯的蒙特卡洛预测结果: alpha = 2
一等奖4,29号;特等奖25号
当然,这是使用了不同的先验强度alpha值出来的三种结果; 我们正常可以直接使用alpha=1最常见的情况。对应贝叶斯种中的均匀先验分布
那么最终的中奖预测为:
至此,再也不用担心每次抽奖只能拿着阳光普照了。