一、基本概念

1.1 什么是特征点？

特征点是图像中具有独特性、可重复性、稳定性的点，如角点、边缘点、斑点等。

1.2 特征描述符（Feature Descriptor）

对特征点周围区域进行描述的数字向量，用于特征匹配，相当于特征点的身份证。

1.3 常用方法

1. 1. Harris角点检测 - 基于灰度梯度变化
2. 2. SIFT（尺度不变特征变换） 尺度、旋转不变性
3. 3. SURF（加速稳健特征） SIFT的快速版本
4. 4. ORB（Oriented FAST and Rotated BRIEF） FAST关键点+BRIEF描述符

二、特征点检测算法原理

2.1 Harris角点检测

核心思想

Harris角点检测基于局部窗口内的灰度变化来检测角点。角点的定义是：在所有方向上灰度变化都很大的点。

算法步骤

1. 1. 计算图像梯度 
2. 2. 计算梯度乘积：
   

1. 3. 高斯加权：
2. 

1. 4. 计算每个像素的Harris响应 R
2. 5. 非极大值抑制：在3×3邻域内比较R值
3. 6. 阈值处理：保留R > threshold的点

import cv2import numpy as npimport matplotlib.pyplot as pltdef harris_corner_detection(img_path, blockSize=2, ksize=3, k=0.04):"""    Harris角点检测原理：    1. 计算图像梯度Ix, Iy    2. 构建结构张量 M = ∑[Ix²  IxIy]                    [IxIy Iy²]    3. 计算响应函数 R = det(M) - k*trace(M)²    4. R > threshold 的点为角点    """    img = cv2.imread(img_path, 0)# 1. 计算梯度    Ix = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=ksize)    Iy = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=ksize)# 2. 计算结构张量的元素    Ix2 = Ix**2    Iy2 = Iy**2    Ixy = Ix * Iy# 3. 高斯加权    Sx2 = cv2.GaussianBlur(Ix2, (blockSize, blockSize), 0)    Sy2 = cv2.GaussianBlur(Iy2, (blockSize, blockSize), 0)    Sxy = cv2.GaussianBlur(Ixy, (blockSize, blockSize), 0)# 4. 计算响应函数    detM = Sx2 * Sy2 - Sxy**2    traceM = Sx2 + Sy2    R = detM - k * traceM**2# 5. 非极大值抑制    R = cv2.dilate(R, None)    threshold = 0.01 * R.max()    corners = np.where(R > threshold)return corners, R, img# 使用示例corners, R, img = harris_corner_detection('test.jpg')plt.figure(figsize=(12, 4))plt.subplot(131), plt.imshow(img, cmap='gray'), plt.title('Original')plt.subplot(132), plt.imshow(R, cmap='hot'), plt.title('Harris Response')plt.subplot(133), plt.imshow(img, cmap='gray')plt.scatter(corners[1], corners[0], c='r', s=10, alpha=0.5)plt.title('Detected Corners')plt.tight_layout()plt.show()

2.2 SIFT（尺度不变特征变换）

SIFT旨在解决尺度、旋转、光照、视角变化下的特征匹配问题。

尺度空间极值检测

1. 高斯尺度空间构建图像 的尺度空间定义为：其中高斯核：

2. 高斯金字塔构建

每个octave（组）的处理：

1. 1. 初始图像通过σ0模糊。
2. 2. 每层通过)模糊，其中S为每octave层数。
3. 3. 下一个octave由上一个octave进行降采样得到（尺寸减半）。

3. DoG（Difference of Gaussian）金字塔

4. 极值检测在3×3×3的邻域（空间+尺度）中寻找局部极值：

• • 中间层像素与相邻26个点比较。
• • 既是极大值又是极小值的点作为候选关键点。

关键点精确定位

1. DoG函数泰勒展开

2. 极值点精确定位求解导数为零的位置：

3. 去除不稳定点

• • 低对比度点：（归一化后）。
• • 边缘响应点：使用Hessian矩阵特征值比值判断。

对于Hessian矩阵：

设特征值 ：

若 ，判定为边缘点并剔除。

方向分配

1. 计算梯度幅值和方向在关键点所在尺度的高斯模糊图像上：

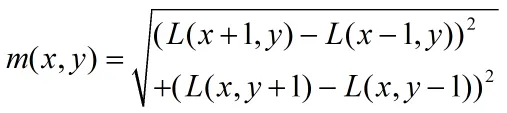
2. 创建方向直方图

• • 以关键点为中心，半径  的区域。
• • 36个bin，每个bin 10度。
• • 用高斯加权梯度幅值投票。

3. 分配主方向

• • 直方图峰值作为主方向。
• • 大于峰值80%的其他峰值作为辅方向。

关键点描述符生成

1. 坐标旋转将坐标轴旋转到关键点方向，确保旋转不变性。

2. 区域划分

• • 以关键点为中心的16×16窗口。
• • 划分为4×4=16个子区域。
• • 每个子区域4×4像素。

3. 计算子区域梯度直方图

• • 每个子区域计算8方向梯度直方图。
• • 用高斯加权梯度幅值投票。
• • 每个关键点得到16×8=128维向量。

4. 描述符归一化

• • 提高对光照变化的鲁棒性。
• • 截断大于0.2的值，重新归一化（增强对非线性光照的鲁棒性）。

def sift_feature_matching(img1_gray, img2_gray, img1_rgb, img2_rgb,                          n_features=500, use_flann=True, ransac_thresh=5.0):    """
    SIFT特征检测与匹配
    """
    # 初始化SIFT检测器
    sift = cv2.SIFT_create(nfeatures=n_features)
    
    # 检测关键点和计算描述符
    kp1, des1 = sift.detectAndCompute(img1_gray, None)
    kp2, des2 = sift.detectAndCompute(img2_gray, None)
    
    print(f"图像1检测到 {len(kp1)} 个关键点")
    print(f"图像2检测到 {len(kp2)} 个关键点")
    
    # 特征匹配
    if use_flann:
        # FLANN匹配器
        FLANN_INDEX_KDTREE = 1
        index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
        search_params = dict(checks=50)
        flann = cv2.FlannBasedMatcher(index_params, search_params)
        matches = flann.knnMatch(des1, des2, k=2)
    else:
        # 暴力匹配器
        bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=False)
        matches = bf.knnMatch(des1, des2, k=2)
    
    # 应用Lowe's比率测试筛选好的匹配
    good_matches = []
    for m, n in matches:
        if m.distance < 0.7 * n.distance:
            good_matches.append(m)
    
    print(f"筛选后得到 {len(good_matches)} 个匹配对")
    
    # 使用RANSAC去除误匹配
    if len(good_matches) > 4:
        src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
        dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
        
        # 计算单应性矩阵
        M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, ransac_thresh)
        mask = mask.ravel().tolist()
        
        # 筛选RANSAC内点
        inlier_matches = [good_matches[i] for i in range(len(good_matches)) if mask[i]]
        print(f"RANSAC后得到 {len(inlier_matches)} 个内点匹配")
    else:
        inlier_matches = good_matches
        print("匹配点太少，跳过RANSAC")
    
    return kp1, kp2, des1, des2, good_matches, inlier_matches

2.3 SURF（加速稳健特征）SIFT的快速版本

积分图像加速

积分图像:

任意矩形区域求和：

其中：

• • 
• • 
• • 
• • 

盒子滤波器近似Hessian矩阵

近似二阶高斯导数：

Hessian行列式：

尺度空间构建

• • 保持图像大小不变，改变滤波器尺寸。
• • 滤波器尺寸：
• • 每个octave包含多个scale。

算法步骤

1. 特征点检测

1. 1. 计算积分图像。
2. 2. 构建尺度空间（不同尺寸盒子滤波器）。
3. 3. 计算Hessian响应。
4. 4. 3D非极大值抑制。
5. 5. 插值精确定位。

2. 方向分配

1. 1. 计算Haar小波响应。
2. 2. 高斯加权。
3. 3. 计算主方向：

3. 描述符生成

1. 1. 划分4×4子区域。
2. 2. 每个子区域计算：
• • 
• • 
3. 3. 得到4×4×4=64维描述符（扩展版本为128维）。

defsurf_detection_opencv(image, hessian_threshold=100, extended=False, upright=False):"""    使用OpenCV实现SURF特征检测    参数:        image: 输入图像        hessian_threshold: Hessian阈值        extended: 是否使用扩展描述符(128维)        upright: 是否不使用方向不变性    """# OpenCV<4.5    surf = cv2.xfeatures2d.SURF_create(    hessianThreshold=hessian_threshold,    nOctaves=4,    nOctaveLayers=3,    extended=extended,    upright=upright)# 检测关键点和计算描述符    keypoints, descriptors = surf.detectAndCompute(image, None)return keypoints, descriptors

2.4 ORB（Oriented FAST and Rotated BRIEF）

FAST检测原理：

方向分配：

计算质心：质心：方向：

rBRIEF（Rotated BRIEF）

1. 1. 在31×31的窗口内。
2. 2. 随机选择256对点 
3. 3. 比较亮度：

1. 4. 得到256位二进制描述符。

旋转不变性改进：

1. 1. 使用方向  旋转点对:

1. 2. 学习最优点对（最大化方差，最小化相关性）。

算法流程

1. 1. oFAST检测：检测关键点并计算方向。
2. 2. 金字塔尺度：构建图像金字塔实现尺度不变性。
3. 3. rBRIEF描述：生成旋转不变的二进制描述符。
4. 4. 特征匹配：使用汉明距离。

classORBFeatureDetector:"""    ORB算法特点：    1. FAST角点检测    2. 计算方向（灰度质心法）    3. rBRIEF描述符    """def __init__(self, n_features=500, scale_factor=1.2, n_levels=8):self.n_features = n_featuresself.scale_factor = scale_factorself.n_levels = n_levelsdef detect_and_compute(self, img):        orb = cv2.ORB_create(            nfeatures=self.n_features,            scaleFactor=self.scale_factor,            nlevels=self.n_levels        )        keypoints, descriptors = orb.detectAndCompute(img, None)return keypoints, descriptors

三、特征匹配算法

3.1 暴力匹配（Brute-Force）

暴力匹配是最直接的特征匹配方法，通过穷举搜索找到最佳匹配。

匹配过程

距离度量

对于两个特征描述符向量  和 ：

1. 欧氏距离（L2距离）：适用于：SIFT、SURF（浮点型描述符）

2. 汉明距离：适用于：ORB、BRIEF（二进制描述符）

3. 曼哈顿距离（L1距离）：

匹配策略

1. 最近邻匹配：

• • 对于查询描述符
• • 在目标集中找到距离最小的描述符
• • 匹配对：

2. 最近邻距离比（NNDR）：

• • 找到最近邻  和次近邻 
• • 计算比值：
• • 阈值判断：通常  或 

3. 数学原理：设查询特征，目标特征集

1. 1. 计算所有距离：
2. 2. 排序：
3. 3. 判断：

算法步骤

1. 1. 对每个查询特征描述符：a. 计算与所有目标描述符的距离。b. 找到最近邻和次近邻。c. 如果使用NNDR：计算比值并判断。d. 记录匹配对。
2. 2. 可选：交叉验证（Cross-check）
• • 双向匹配：A→B和B→A。
• • 保留双向一致的匹配。

classFeatureMatcher:def __init__(self, method='BF', norm_type=cv2.NORM_L2):self.method = methodself.norm_type = norm_typedef brute_force_match(self, desc1, desc2, ratio_test=0.75):"""        暴力匹配原理：        1. 计算desc1中每个描述符与desc2中所有描述符的距离        2. 选择距离最近的两个匹配        3. 应用比率测试：d1/d2 < ratio_test        """if desc1 isNoneor desc2 isNone:return []if self.norm_type == cv2.NORM_HAMMING:# 用于二进制描述符（ORB, BRIEF等）            matcher = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=False)else:# 用于浮点描述符（SIFT, SURF等）            matcher = cv2.BFMatcher(cv2.NORM_L2, crossCheck=False)# 执行knn匹配（k=2）        matches = matcher.knnMatch(desc1, desc2, k=2)# 应用比率测试        good_matches = []for m, n in matches:if m.distance < ratio_test * n.distance:                good_matches.append(m)return good_matches

3.2 FLANN（快速最近邻搜索）

FLANN通过近似最近邻搜索加速匹配过程，牺牲少量精度换取速度的大幅提升。

主要算法

KD-Tree（k维树）

1. 构建过程：

算法：BuildKDTree(points, depth)。输入：点集points，当前深度depth输出：KD-Tree根节点

1. 1. 如果points为空：返回空节点
2. 2. 选择划分维度：axis = depth mod k
3. 3. 按axis维度排序points
4. 4. 选择中位数点作为根节点
5. 5. 递归构建左子树（points[:median]）
6. 6. 递归构建右子树（points[median+1:]）

2. 搜索过程：

算法：SearchKDTree(node, query, best)输入：当前节点node，查询点query，当前最佳best输出：最近邻点

1. 1. 如果node为空：返回best
2. 2. 计算node与query的距离，更新best
3. 3. 确定搜索方向：
• • 如果：先搜索左子树
• • 否则：先搜索右子树
4. 4. 搜索优先子树
5. 5. 检查另一子树（如果可能包含更近的点）：
• • 如果
• • 则搜索另一子树

3. 多重KD-Tree：

• • 构建多个不同的KD-Tree（随机选择划分维度）
• • 并行搜索所有树
• • 取最佳结果

K-Means树

1. 构建过程：

1. 1. 初始：将所有点作为一个簇
2. 2. 重复直到达到深度限制：a. 对每个簇，使用K-Means聚类为K个子簇（通常K=16）b. 将簇中心作为树的节点c. 将点分配到最近的子簇

2. 搜索过程：

• • 从根节点开始
• • 选择距离查询点最近的簇中心
• • 递归搜索，直到叶节点
• • 回溯检查其他可能分支

3 层次聚类树（Hierarchical K-Means）

结合KD-Tree和K-Means的优点：

1. 1. 顶层使用KD-Tree快速划分
2. 2. 底层使用K-Means精细聚类
3. 3. 自适应选择划分策略

近似最近邻搜索原理

ε-近似最近邻：设真实最近邻距离为 ，算法找到的距离为 满足：

概率近似最近邻：以概率  找到最近邻

defflann_match(self, desc1, desc2, ratio_test=0.7):"""    FLANN匹配原理：    使用kd-tree等数据结构加速最近邻搜索     """if desc1.dtype == np.uint8:         二进制描述符         index_params = dict(algorithm=6,  # FLANN_INDEX_LSH                                table_number=6,                                key_size=12,                                multi_probe_level=1)else:# 浮点描述符        index_params = dict(algorithm=1, tree=5)    search_params = dict(checks=50)       flann = cv2.FlannBasedMatcher(index_params, search_params)    matches = flann.knnMatch(desc1, desc2, k=2)    good_matches = []for m, n in matches:if m.distance < ratio_test * n.distance:            good_matches.append(m)return good_matches

3. RANSAC（随机抽样一致性）

RANSAC通过随机采样和一致性验证来估计模型参数，有效处理异常值（误匹配）。

基本概念

• • 内点（Inliers）：符合模型的数据点
• • 外点（Outliers）：不符合模型的异常点
• • 最小样本集（MSS）：估计模型所需的最小数据点数

算法流程

输入：data - 数据点集（包含异常值）model - 待估计的数学模型n - 最小样本集大小k - 最大迭代次数t - 内点阈值d - 内点数阈值

输出：best_model - 最佳模型参数best_consensus_set - 最佳内点集

算法步骤：

1. 1. best_model = None
2. 2. best_consensus_set = ∅
3. 3. best_inlier_count = 0
4. 4. 重复k次：a. 随机选择n个点作为最小样本集b. 根据最小样本集估计模型参数model_ic. 对每个数据点：
• • 计算误差error = 点到模型的距离
• • 如果error < t：标记为内点d. 统计内点数量inlier_counte. 如果inlier_count > d：
• • 使用所有内点重新估计模型参数
• • 如果新模型更好：更新最佳模型f. 如果inlier_count > best_inlier_count：
• • 更新best_inlier_count
• • 更新best_consensus_set
5. 5. 返回best_model, best_consensus_set

迭代次数计算

迭代次数  的选择基于概率：

其中：

• • ：期望的成功概率（通常0.99）
• • ：内点比例（先验估计或自适应估计）
• • ：最小样本集大小

四. 算法比较总结

特征点检测算法总结

特征匹配算法总结

实际应用建议

1. 1. 实时应用：
• • 检测：ORB
• • 匹配：FLANN + 汉明距离
2. 2. 高精度应用：
• • 检测：SIFT
• • 匹配：暴力匹配 + RANSAC
3. 3. 平衡应用：
• • 检测：SURF
• • 匹配：FLANN + RANSAC
4. 4. 计算资源有限：
• • 检测：Harris/ORB
• • 匹配：暴力匹配

每种方法都有其适用场景，需要根据具体应用需求、计算资源和精度要求进行选择。实际应用中常采用多种方法组合，如使用FLANN进行快速初匹配，再用RANSAC进行误匹配剔除。