C语言有没有那种惊为天人的优雅代码?有。
那就是天才程序员约翰·卡马克(JohnCarmack)为《雷神之锤III竞技场》写的平方根倒数速算法(Fast Inverse Square Root,FastInvSqrt() )。
这是一段改变计算机游戏史的魔法代码。
这段代码配得上惊为天人。
今天就来讲讲这段代码,会涉及到一些数学方面的知识,我尽量用通俗易懂的大白话来描述。
一、什么是平方根倒数?
平方根倒数即:
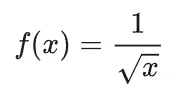
那么,如何写出实现这段公式的C语言代码?
你可能和我一样,觉得这有什么难的,一行代码就可以搞掂:
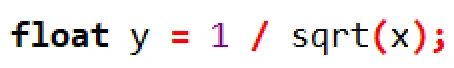
一行代码,先开平方再除法,其中开方和除法都是非常耗时的操作。
然而,在公开的《雷神之锤III竞技场》源代码中,我们看到卡马克是这样写的:
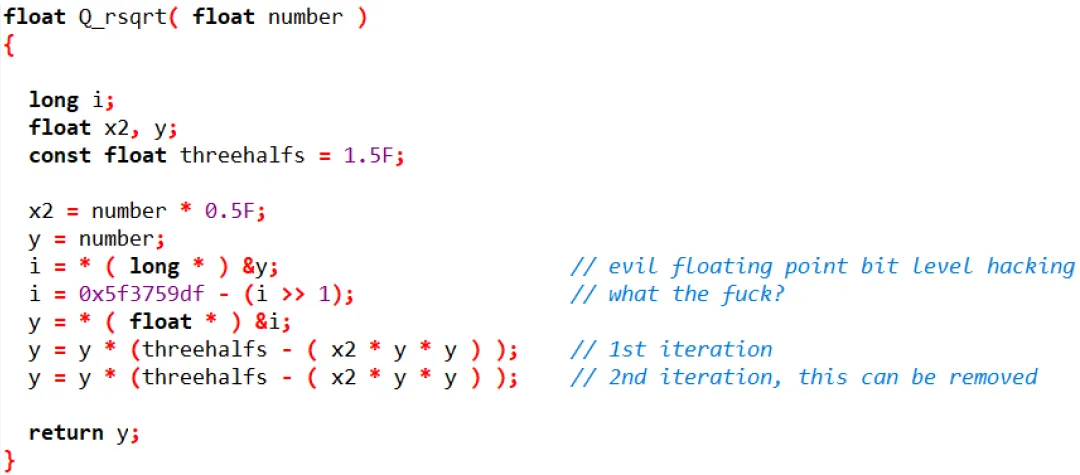
注意其中有一行的注释是:
what the fuck? 什么鬼?
其中的魔术数字0x5f3759df到底是什么鬼??
这个神秘的特殊常数是哪里来的???
二、魔法代码揭秘
现在我们来分析《雷神之锤3》的这段原始代码。
第一步:整数近似(魔法核心)

用到了右移运算符>>,i>>1是右移1位;
关键的魔法公式:
i =0x5f3759df-(i >>1);
以及:
i =*(long*)&y;
这是类型双关,是浮点数转成整数的关键。
揭秘:
1.浮点数的IEEE 754表示:32位浮点数 = 1位符号 + 8位指数 + 23位尾数;
2.对数近似:log₂(√x) = ½ log₂(x);
3.整数减法代替浮点除法:在指数域中,除以2等于右移1位。
魔法数0x5f3759df推导:
魔数 ≈ 1.5 × 2²³ × (127 - 0.043)
其中127是IEEE 754的指数偏移量,0.043是修正项。
第二步:类型转换回浮点数
y =*(float*)&i;是整数转成浮点数, y 已是 1/√x 的近似值,误差约1%。
第三步:牛顿迭代法精修
迭代两次(下面这条语句写了两次):
y = y *(threehalfs -(x2 * y * y));
使用牛顿法求解 f(y) = 1/y² - x = 0,结果:
一次迭代精度达99.8%,两次迭代达99.99%。
三、数学推导
1. 浮点数的对数表示
IEEE 754浮点数:
浮点数 F = (1 + m) × 2^{e-127}
取对数:log₂(F) ≈ e - 127 + m
其中 m = 尾数/2²³,范围[0, 1)。
2. 整数表示视角
将浮点数按位解释为整数:
整数 I = 2²³ × e + 尾数
=2²³ × (log₂(F) + 127 - m) + 2²³ × m
≈2²³ × log₂(F) + 2²³ × 127
3. 推导魔法公式
计算 y = 1/√x:
log₂(y) = log₂(1/√x) = -½ log₂(x)
用整数近似:
I_y ≈ 2²³ × (-½ log₂(x)) + 2²³ × 127
=2²³ × 127 - ½ × (2²³ × log₂(x) + 2²³ × 127 - 2²³ × 127) + ½ × 2²³ × 127
=1.5 × 2²³ × 127 - ½ × I_x
得到:
I_y = 0x5f3759df - (I_x >> 1)
其中 0x5f3759df = 1.5 × 2²³ × 127 + 修正项。
以下是测试程序示例。
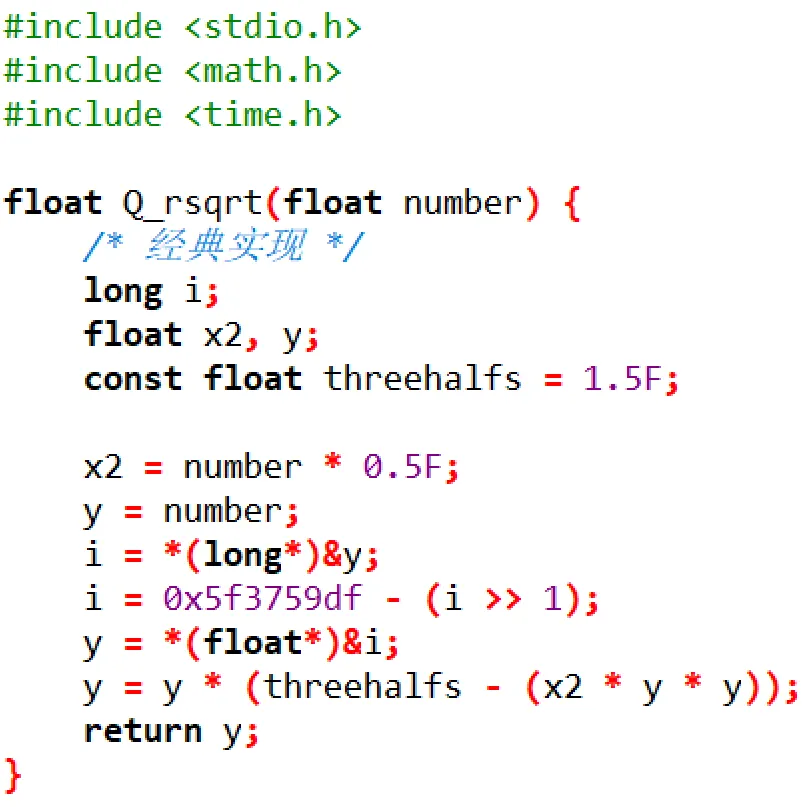

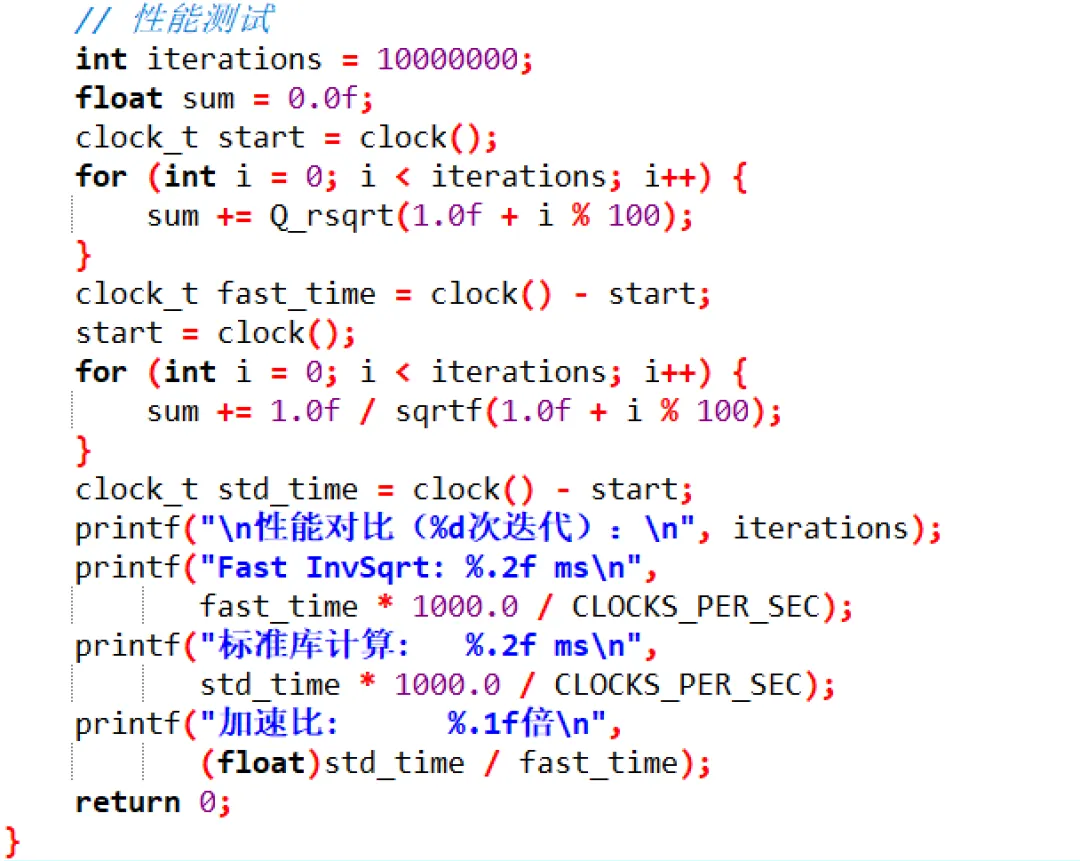
运行结果:
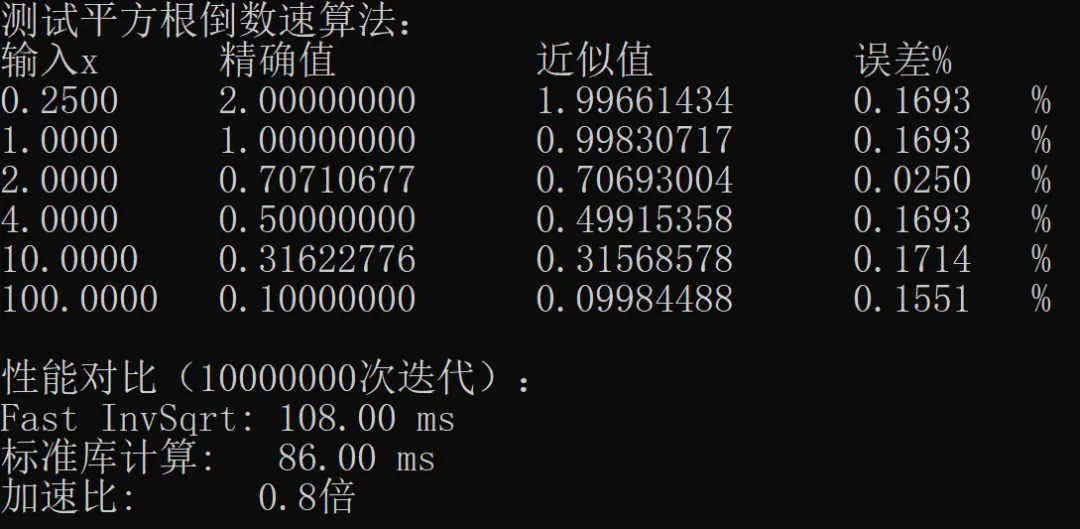
从运行结果看,天才程序员卡马克写的算法效率高于标准库算法。
四、优化的哲学
真正突破性的优化,往往来自于对计算机系统的深刻理解,以及打破常规的勇气。
这个算法对图形运算具有非凡的意义,体现在:
·图形学革命:使实时3D游戏在90年代硬件上成为可能。
·算法思维典范:展示了硬件层级的优化思维。
·文化现象:成为程序员间广为流传的黑魔法。
在3D图形学中,这个求平方根倒数计算无处不在,如:
·向量归一化(计算单位向量);
·光照计算;
·物理模拟;
·声音处理。
虽然现代硬件已有优化,但该算法仍适用于:
·嵌入式系统(无浮点单元);
·需要确定性的场景(避免不同硬件差异);
·算法教学(数值分析、优化技巧)。
平方根倒数速算法已经远远超越了它的实用价值,它象征着:
1.深入理解硬件的重要性;
2.跨层优化的威力(从数学理论到位操作);
3.创造性思维对性能的关键影响。
阿瑟·克拉克说:任何足够先进的技术,初看都与魔法无异。
这个算法所代表的优化哲学,值得每一位程序员学习与传承。
结语
也许那些数学推导你不熟悉,但只需记住:
比起用1/sqrt(x)来求平方根倒数,天才程序员约翰·卡马克的平方根倒数速算法简直是天外飞仙,它大大减少了浮点运算操作带来的巨大运算消耗。
而魔术数字0x5f3759df在很长一段时间内一直被无数程序员津津乐道,也一直有人在探寻:
卡马克究竟是怎么想出来这个数字的?
这段代码,简洁而高效,让人忍不住为天才的智慧击节叫好,叹为观止。