算法代码速成25:经典SIR传染病模型:微分方程组的建立与编程求解

1.SIR模型概念和术语

SIR模型将人群分为三类：

S(t)：易感者（Susceptible），未感染但可能被传染的个体数量。

I(t)：感染者（Infectious），已感染并可传播疾病的个体数量。

R(t)：康复者（移除态）（Recovered），康复后不再参与传播的个体数量。

感染率：β表示假设一个易感者在单位时间里与感染者接触并被传染的概率。

康复率（移除率）：γ表示一个感染者单位时间转化为康复（移除）状态的概率。

2.SIR模型原理与假设

a.总人数不变：N=S(t)+I(t)+R(t)，忽略出生、死亡、迁移。

b.流行病传播过程：易感者—>感染者—>康复者。

c.易感者群体减少的数量=感染者群体增加的数量。

d.康复者群体增加的数量=感染者群体减少的数量。

e.感染者群体变化的数量=易感者+康复者变化之和。

3.SIR模型

SIR模型的微分方程组形式：

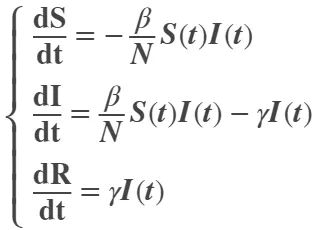
该模型包含三个变量S，I，R，三个参数N，β，γ。

4.SIR模型的应用方法

（1）预测趋势：根据实际问题运用统计学方法或者其他方法，估算或者假设参数N，β，γ，然后求解S，I，R，预测易感者、感染者和感染者随着时间t的变化趋势，用于指导制定相应的政策措施。

（2）参数辨识：已经收集易感者S、感染者I和感染者R随着时间t的变化的大量数据，对模型进行参数辨识，识别三个参数N（可选），β，γ，分析感染率和康复率的水平。

（3）常用：参数辨识—>预测趋势。

5.预测趋势（编程示例）

假设总人数：N = 1000 ，感染率β= 0.3，康复率γ=0.1。

建立SIR模型，给出流行病传播动态模拟变化预测趋势图。

Matlab程序代码如下：

tspan = [0 100];

Y0=[999;1;0];

[t, Y] = ode45(@sirmoxing, tspan, Y0);

plot(t, Y(:,1), 'b', t, Y(:,2), 'r', t, Y(:,3), 'g', 'LineWidth', 2);

xlabel('时间（天）');

ylabel('人数');

legend('易感者 S(t)', '感染者 I(t)', '康复者 R(t)');

title('SIR模型动态模拟');

grid on;

function dYdt = sirmoxing (t, Y)

N = 1000;% 总人口

beta = 0.3;% 感染率

gamma = 0.1;% 康复率

S = Y(1);

I = Y(2);

R = Y(3);

dSdt = -beta * S * I / N;

dIdt = beta * S * I / N - gamma * I;

dRdt = gamma * I;

dYdt = [dSdt; dIdt; dRdt];

end

运行结果如下：

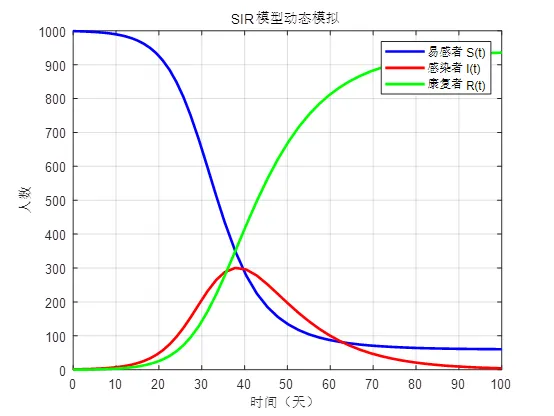
6.结合实际问题进行分析预测

以新冠疫情为例，易感者呈下降趋势，康复者呈上升趋势，感染者先增多后减少，与实际问题的发展变化规律相符。

另外，可以提取感染者群体中最大值所在的时间点，也就是拐点的位置，感染者群体经拐点后呈下降态势，有利于对防控政策的调整和实施起到指导建议作用。大家可根据自己研究的问题做具体深入的分析。

【参考视频14.12，B站搜freexyn有视频】

相关推荐