第5章 函数
前面我们介绍的代码都是从上到下执行的顺序结构,只不过有些语句是条件、有些是循环而已,总体是顺序执行的。但在一个大型的应用程序中,需要在不同的位置大量地使用相同的代码来完成特定的功能,如果完成某个特定功能的代码比较复杂,代码很长,程序中需要使用很多次(如前面介绍的print()、input()、sum()等),这时,如还是使用前面介绍的方法,一方面将大大加大程序的代码量,另一方面当代码中存在bug需要修改时,所有的代码都必须一一修改,大大增加了程序维护的难度。因此程序设计中都提供了函数的概念,将需要大量使用的相同代码,用一个特定的函数定义出来,程序需要使用时,只需要在需使用的位置调用该函数即可,这样不仅可以大大缩短程序代码量,而且大大方便地代码的维护,所以程序设计中函数的应用非常广泛,也非常重要。如前面介绍的print()、input()等函数系统没有提供的话,要程序设计者自己编写的话,则全世界恐怕没有几个人能胜任程序设计的任务。
Python中函数分为内置函数(如input()、print()等)、模块函数(random.randint()等)和自定义函数。
函数是一个能完成特定功能的代码块,可在程序中重复使用,从而减少程序的代码量、提高程序的执行效率。
5.1 函数定义:
内置函数随Python系统启动就已调入,所有可以直接使用。模块函数是指在特定模块中定义的函数,也分成两类:内部模块和和外部模块,要使用内部模块中的函数,必须先导入模块,然后再调用模块中定义的函数,而外部模块必须先在系统中完成安装,然后就可以与内部模块中的函数一样导入和调用了。自定义函数就是本章介绍的重点。
Python自定义函数的定义格式:
def 函数名([形式参数1, 形式参数2[, ...]]):
语句
[return [返回值]]
函数定义中形式参数和返回值不是必须的。如果没有return语句,或没有返回值,则函数返回None。
函数名后()内的称为形参列表,用于设置可以接收多少个参数,参数之间用逗号( , )分隔。形参的个数每个函数定义时一般都不一样,一些函数可能没有形参,此时该函数便称为无参函数。需要注意:即使函数没有参数,也必须在函数名后保留一对空的“()”。
例5-1:编制一个函数,求n!
编程分析:
根据阶乘的数学定义,n! = 1*2*3*......*n。这显然可以用一个循环语句完成:循环变量i的初值为1,终值为n,每次加1,循环前设置阶乘值f = 1;循环体执行 f = f * i 便可完成。
因n!可能在程序中被调用多次,因此将上述步骤设计为一个函数,从上述分析中可以看到,完成n!计算的代码段中设计时只有一个数据是不确定的,那便是n,所以设计函数时,将n设置为该函数的形参。
据此,求n!的函数定义如下:
deffact(n): # 定义函数fact,形参为n f = 1 # 阶乘的初值为1 for i inrange(1, n+1): # i值从2变化到n f *= i # f = f * i , 通过循环将乘积累积为1*2*3*......*n return f # 返回 n! 的值
5.2 函数的调用
调用自定义函数之前,须先创建该函数。
Python中的内置函数可以直接调用。模块中的函数需要先导入该模块,然后调用模块函数。
函数定义后,不表示定义后,程序执行时就可以按以前介绍的那样,按从上到下就可执行到它,函数要在程序中被执行到,就必须在程序中调用它。调用方法如下:
函数名([实际参数1, 实际参数2[, ...]])
调用时,实际参数1、实际参数2等对应该函数定义时的形式参数,一般定义是几个,调用时也是几个。定义时是无参函数,调用时也必须将函数名后的()写上。
针对例5-1中定义的fact(n)函数,就可以在程序中调用它,调用前,先输入n的值,表示要求n!的值,调用后将函数的返回值赋值给一个变量,然后输出即可(也可以在输出时,输出值中直接调用该函数)。例5-1的完整代码如下所示:
deffact(n): # 定义函数fact,形参为n f = 1 # 阶乘的初值为1 for i inrange(1, n+1): # i值从2变化到n f *= i # f = f * i , 通过循环将乘积累积为1*2*3*......*n return f # 返回 n! 的值n = int(input('请输入n='))e = fact(n) # 调用fact()函数,返回的函数值赋值给eprint(f'{n}!={e}') # 也可以直接在输出函数中调用: print(f'{n}!={fact(n)}')
程序通过函数调用来进行相互间数据的传递并控制执行该函数中定义的语句。
如例5-1中,e = fact(n)赋值语句中,赋值号右边的fact(n)就是一个fact()函数的调用。表示在求出n!的值后,将该函数的返回值赋值给e变量。
例5-2:求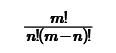 表达式的值
表达式的值
编程分析:
在上述表达式中,有3个求阶乘的操作。因此可以编制一个求阶乘的函数,再通过调用该函数求上述表达式的值。
上述表达式中有2个末知数m和n,因此先通过input()输入m和n的值并转换成整数后,分3次调用求阶乘函数,分子上fact(m),分母上是fact(n)和fact(m-n),因阶乘的参数一般是正数,因此程序设计时要求m-n>0。
据此,实现上述任务的代码如下:
deffact(n): # 定义函数fact,形参为n f = 1 # 阶乘的初值为1 for i in range(1, n+1): # i =2,3,...,n f *= i # f = f * i , 通过循环将乘积累积为1*2*3*......*n return f # 返回 n! 的值whileTrue: m = int(input('请输入m=')) n = int(input('请输入n=')) if m>n : break # 确保m>ne = fact(m)/fact(n)/fact(m-n) # 调用3次fact()函数,求不同的阶乘值print(e) # 输出表达式结果
5.3 函数的参数
为了方便设计,Python中设置了如下几种形参:
1、位置参数(也称必需参数)
位置参数调用时须以正确的顺序传入函数。调用时的数量与位置必须和声明(定义)时完全一致。
如例5-1中定义的fact(n)函数中,形参n就是一个位置参数,调用时形参个数和位置必须与定义时完全一致,即必须传入有且仅有的一个参数n。因此调用时必须是1个实际参数,不能多也不能少,因此以下调用都是错误的:
fact() # 没有参数
fact(m,n) # 有2个实际参数
例如:定义一个函数,求 x**n 的值。
函数定义如下:
defpower(x, n): # 求 x**n 的值 s = 1 while n > 0: s = s * x # x乘 n 次 n = n - 1 return s # 返回 x**n 的值
power(x, n)函数(实现计算x**n)有两个参数:x和n,这两个参数都是位置参数,调用函数时,传入的两个实际值按照位置顺序依次赋给参数x和n。调用代码可以是:
print(power(2, 5)) # 输出32 (2**5)
例 5-3 【程序功能】定义一个函数f(x, y),x和y表示两个正整数。如x是y的倍数,返回True,否则,返回False。为了验证函数定义的正确性,从键盘上输入三个正整数N、a和b(a小于b),用空格分隔。输出a和b之间(含)是N的倍数的数,多个数之间以空格隔开。
编程分析:
按设计要求,定义的函数f(x, y)有2个位置参数x和y,x是y的倍数,即:x%y==0时返回True,否则返回False。据此函数定义如下面代码中的1-5行所示。
主程序中,通过调用input()函数输入一行数据(N,a,b),数据间用空格分隔,再使用字符串的split()方法将输入的数据分解后,将数据转化为整数,因此可以使用以下列表推导式完成:
N, a, b = [int(x) for x in input().split()]
然后,使用一个for语句,循环变量i从 a 到 b,循环中通过if语句判断调用f(i, N)的返回值决定是否输出 i 的值,如调用f(i, N)的返回值为True,则输出。输出时,使用end=' '参数,使输出的数据间使用空格分隔。据此,实现以上功能的代码设计如下:
deff(x, y): ifx%y==0: # 若整除 returnTrue # 返回True else: returnFalse # 返回False# 使用列表推导式将一行中使用空格分隔的输入数据分解并转化为整数N, a, b = [int(x) for x ininput().split()]for i in range(a, b + 1): # i = a,a+1,....,b # 使用 i, N 实际参数调用f()函数,并根据返回值为True,输出 i 的值 if f(i, N): print(i, end=' ') # end=' ' 输出的数据(为 N 的倍数)之间用空格分隔
代码执行过程如下:
2、默认参数
前面介绍的函数power(x, n)解决了计算x**n问题,但考虑到要经常计算x**2,即参数n为2是最为常见的,此时可采用默认参数来解决这个问题,即默认参数能简化函数的调用。函数定义时,若需使用默认参数,必需参数必须在前,默认参数需要放在必需参数后(即默认参数右边不能再有必需参数)。
调用函数时,默认参数如果没有传递实际参数,则会使用默认值。
要完成上述功能,power()函数可以设计为:
defpower(x, n = 2): # 使用了默认参数n = 2 s = 1 while n > 0: s = s * x # x乘 n 次 n = n - 1 return s # 返回 x**n 的值
power(x, n=2)函数有两个参数:x和n,第一个参数是必需(位置)参数,第二个就是默认参数。
调用函数时,可以只传入一个值x,n使用默认值2,也可以传二个值。如:
print(power(3)) # 输出3**2print(power(3, 5)) # 输出3**5
3、关键字参数
上面介绍函数定义时,形参可以使用位置参数和默认参数,但这两种参数定义时有严格的位置关系,位置参数必须在左测,默认参数须在位置参数右测。函数调用时,也要与定义时一样按严格的顺序来调用,这样给使用带来了一定不便,因此Python提供了使用关键字参数通过形式参数名来确定传入的参数值。
使用关键字参数允许函数调用时参数的顺序与定义时不一致,因为 Python 解释器能够用参数名匹配参数值。这样做有两大优点:其一,不再需要考虑参数的顺序,函数的使用将更加容易。其二,可以只对那些希望赋予的参数以赋值,其它的参数都使用默认参数值。
对于上述定义的power(x, n = 2),可以使用以下关键字参数来方便的调用:
# 使用关键字参数进行函数调用print(power(x=3)) # 明确将3传送给xprint(power(n=5, x=3)) # 明确将5传送给n,3传送给x
4、可变参数 * 和 **
当传入的参数个数是可变的,可以是1个、2个或者任意多个,也可以是0个时,就可以使用可变参数。
当函数定义时在形参名前加上 * 或 ** 时,就表示该形参是可变参数。
⑴ 定义时若在形参名前加上 * ,则调用时,将从此处开始直到结束的所有位置参数都将被收集并打包成元组(Tuple)的方式传送给形参。下面是使用可变参数 *的函数定义实例:
# 函数定义的形参中,*number就是一个可变参数,n是默认参数defcalc(*number, n=2): s = 0 for x in number: # 完成元组number中每个数**n 的累加 s = s + x ** n return s
调用上述定义的calc()函数时,形参接收得到的是一个元组,可以传入任意个参数。n可以有值,也可以没有值。例如:
print(calc(2, 3, 4)) # 将元组(2, 3, 4)传给number,n取默认值2print(calc(2, 3, 4, n=3)) # 将元组(2, 3, 4)传给number,n传值3
⑵ 定义时若在形参名前加上 ** ,则调用时,将从此处开始直至结束的所有关键字参数都将被收集并打包成字典(Dictionary)的方式传送给形参。下面是使用可变参数 ** 的函数定义实例:
''' k是位置参数 *number是可变参数,接受打包成元组的所有位置参数 **phonebook是可变参数,接受打包成字典的所有关键字参数'''deftotal(k, *numbers, **phonebook): print('k:', k) # 输出 k 参数的值 #遍历numbers元组中的所有项目 forsingle_itemin numbers: print('single_item:', single_item) #遍历phonebook字典中的所有项目 forfirst_part, second_part in phonebook.items(): print(first_part,second_part)
调用上述定义的total()函数时,形参k接受一外位置参数,形参numbers接收得到的是一个元组,可以传入任意个位置参数,形参numbers接收得到的是一个字典,可以传入任意个关键字参数。例如:
total(1,2,3,金晓杰=13245308981,顾玲艳='02167333701',刘威=13705816080)total(10,1,2,3,金晓杰=13245308981,顾玲艳='02167333701',刘威=13705816080)
5、参数传递
在 python 中,string、tuple 和 number 是不可更改的对象,而 list、dict 等则是可以修改的对象。
a = 10print( id(a) ) # a变量的地址a = 100print( id(a) )
执行结果为:
1124375921168
1124375924048
可以发现,虽然变量名还是 a,但其地址已变。
可变类型:变量赋值 lia=[10, 20, 30, 40] 后再赋值 lia[2] = 5 则是将 lia 的第三个元素值更改为 5,而本身lia没有任何变化,只是其内部的一部分值被修改了而已。可以通过下面的代码验证。
lia = [10, 20, 30, 40] # 列表 liaprint(id(lia), lia, sep='\t') # lia变量的地址及值lia[2] = 5 # 将 lia 的第三个元素值更改为 5print(id(lia), lia, sep='\t') # lia变量的地址及值
执行结果为:
2928926654912 [10, 20, 30, 40]
2928926654912 [10, 20, 5, 40]
可以发现,修改变量 lia 中元素的值后,其地址是不会改变的,但其值已被修改。
python 函数的参数传递:
def fun( a ): print( id(a), a, sep = '\t') # a变量的地址及值 a = 100 # 修改 a 变量的值 print( id(a), a, sep = '\t') # a变量的地址及值a = 5fun( a )print( id(a), a, sep = '\t') # a变量的地址及值
执行结果为:
2386141315440 5
2386141318480 100
2386141315440 5
可以发现,调用fun( a )时,在修改变量 a 前,其值与函数外的 a 值相同,但修改后其地址就不同了。函数调用后,变量 a 的值还是函数调用前的地址和值,没有任何改变。
def fun( lia ): print( id(lia), lia, sep = '\t') # lia变量的地址及值 lia[2] = 5 # 将 lia 的第三个元素值更改为 5 print( id(lia), lia, sep = '\t') # lia变量的地址及值lia = [10, 20, 30, 40] # 列表 liafun( lia )print( id(lia), lia, sep = '\t') # lia变量的地址及值
执行结果为:
2503721122176 [10, 20, 30, 40]
2503721122176 [10, 20, 5, 40]
2503721122176 [10, 20, 5, 40]
可以发现,调用fun( lia )时,在修改变量 lia 前,其值和地址与函数外的 lia 值和地址相同,但修改后其地址没有任何修改,但其值已改变。函数调用后,变量 lia 的值保留了函数内修改后的结果。
5.4 Lambda函数
lambda关键字用来在同一行内创建函数,这个函数称为匿名函数,也称lambda函数,就是没有实际名称的函数。
语法格式:
lambda 函数可接受任意数量的参数,执行表达式并返回结果。
例如:接受两个数,返回它们的积x*y,则可以定义一个lambda 函数如下:
# 定义匿名函数,有2个形参,返回这2个形参的乘积f = lambda x, y : x * yprint(f(3, 6)) # 调用匿名函数, 输出18
例 5-4 对一个整数列表,按照元素的绝对值大小升序排列。
编程分析:
对于一个整数列表,要对其中的元素进行排序,我们知道可以使用sorted()函数或列表的sort()方法。但题意要求不是按元素的原值排序,而是其绝对值,因此直接使用列表的sort()方法进行排序,是无法完成任务,必须排序时是使用绝对值,而排序后的结果还是原值,因此可以使用列表的sort()方法中的key形参(详细参见列表的排序),给key传递一个lambda函数,送入原值,返回绝对值,即按绝对值排序。
用lambda函数的实现代码如下:
list1 = [3, 5, -4, -1, 0, -2, -6]print(f'排序前的列表:{ list1 }')list1.sort(key = lambda x : abs(x)) # 使用lambda匿名函数,排序时按绝对值print(f'排序后的列表:{ list1 }')
代码执行结果如下:
排序前的列表:[3, 5, -4, -1, 0, -2, -6]
排序后的列表:[0, -1, -2, 3, -4, 5, -6]
通过前面的介绍,我们知道字典是无序的,因此不能直接对字典进行排序。如果需要对字典按照键或值降序排序,可以采取间接的办法,先把字典 d 的键-值对转换为列表,即list( d.items() ),再对列表嵌套的元组按第一项(键)或第二项(值)进行排序,就可以使用 lambda函数 可以方便的获取元组的第一项或第一项:lambda k : k[0]。实现代码如下:
d = {'f': 10, 'g': 1, 'a': 18, 'c': 12, 'e': 16, 'd': 7, 'b': 16}print(f'排序前的字典:{d}')list_d = list(d.items())list_d.sort( key=lambda k:k[0], reverse=True ) # 按key降序排序d_sorted = dict( list_d )print(f'按key排序后的字典:{d_sorted}')list_d.sort( key=lambda k:k[1], reverse=True ) # 按值降序排序d_sorted = dict( list_d )print(f'按值排序后的字典:{d_sorted}')
代码执行结果如下:
排序前的字典:{'f': 10, 'g': 1, 'a': 18, 'c': 12, 'e': 16, 'd': 7, 'b': 16}
按key排序后的字典:{'g': 1, 'f': 10, 'e': 16, 'd': 7, 'c': 12, 'b': 16, 'a': 18}
按值排序后的字典:{'a': 18, 'e': 16, 'b': 16, 'c': 12, 'f': 10, 'd': 7, 'g': 1}
从执行结果输出中可以看出,按key排序后的字典是原字典按键降序排序后的结果,同样按值排序后的字典是原字典按值降序排序后的结果。
5.5 变量的作用域
变量的作用域是指在程序中明确该变量能操作的有效范围。根据作用域的不同,变量分为局部变量和全局变量。
在一个函数内为变量赋值,则该变量就为局部变量。局部变量的作用域仅限于定义它的函数体中,任意一个函数都不能访问其他函数中定义的局部变量。
在所有函数之外定义的变量称为全局变量,它可以在其定义后的多个函数中被引用。
在Python 中,当同名变量在函数外和函数内都存在时,仅在函数内引用(赋值号后表达式中)的变量是隐式全局变量。如果在函数体内的任何位置为变量赋值,则除非明确声明为全局,否则将其视为局部变量。
例如:
a = 10 # 全局变量a, bb = 20def fun(): a = 1 #fun()函数内定义的局部变量a(赋值号前),不会改变全局变量 a 的值 #fun()函数内使用了全局变量b print(f"函数内: a={a},b={b}")print(f"调用函数前: a={a},b={b}")fun() # 调用fun()函数print(f"调用函数后: a={a},b={b}")
代码执行结果如下:
调用函数前: a=10,b=20
函数内: a=1,b=20
调用函数后: a=10,b=20
如果需要在函数内部使用全局变量时,可以使用global语句声明。如下面的代码:
def fun(): global a # 说明本函数内 a 变量是全局变量 a a = 1 # 全局变量 a 赋值1 b = 2 # fun()函数内定义的局部变量b print(f"函数内: a={a},b={b}")a = 10 # 函数外定义的全局变量 a, bb = 20print(f"调用函数前: a={a},b={b}")fun() # 调用fun()函数print(f"调用函数后: a={a},b={b}") # 输出:调用函数后: a=1,b=20。发现全局变量 a 的值已为1
代码执行结果如下:
调用函数前: a=10,b=20
函数内: a=1,b=2
调用函数后: a=1,b=20
主程序中在第10行调用了fun()函数,因fun()函数内使用global a 语句将本函数内的 a 说明为全局的,因此在执行fun()函数的第3行时,将全局变量 a 的值修改为1,而第4行的变量 b 还是局部的。所以函数调用结束后,第11的print()输出时,变量 a 的值输出是1,而 b 还是20。
5.6 函数的递归(recursion)
递归是一种直接或者间接调用函数自身的算法。其本质是把问题分解成规模缩小的同类子问题,然后递归调用获得问题的解。
能够设计成递归算法的问题必须满足两个条件:
1、能找到反复执行的过程(调用自身)
2、能找到跳出反复执行过程的条件(递归出口)。
例5-5:求 n! 的值
编程分析:
n!的数学公式可以定义为:
从该公式中可以清晰地看到其是反复地调用求阶乘的操作(即调用自身),即:fact(n) = n*fact(n-1),直到参数的值为1为止(即递归出口),因此该功能可以使用递归来实现,相关实现代码如下所示:
deffact(n): # n! ifn==1: # 递归出口 return1 else: return n * fact(n-1) # 反复调用m = int(input('请输入m='))print(f'{m}!={fact(m)}') # 调用函数并输出返回值m!
代码执行过程如下:
例 5-6 设计一个f(n)函数,n是一个正整数,f(n)的功能是求n的阶乘。为了验证函数的正确性,从键盘上输入以空格隔开的若干个正整数,计算并输出这些正整数的阶乘之和。
编程分析:
求n!的函数可以直接使用例 5-6 的代码。题目要求输入以空格隔开的若干个正整数,因此,可以将字符串分解split()和字符串转化成整数这二个操作整合到列表推导式中产生一个整数列表,然后通过一个求累加和的循环完成这些数的阶乘之和,相关实现代码如下:
deff(n): # n! ifn==1: # 递归出口 return1 else: return n * f(n-1) # 反复调用s = 0#将输入的以空格隔开的若干个正整数字符串进行分解split()list_line_num = input().split() # 转化成整数列表nums = [int(x) for x in list_line_num]formin nums: s = s + f(m) # 调用函数并完成累加print(f'{"!+".join(list_line_num)}!={s}') # 输出累加和
代码执行过程如下:
例 5-7 编写一个函数,功能是计算传入列表的最大值、最小值和平均值,然后调用该函数输出计算结果。
编程分析:
前面介绍的函数中,return通常只返回一个值。但Python中对返回值的类型没有限制,因此,可以通过返回一个元组类型来间接达到返回多个值的目的。返回的元组可以省略括号,而多个变量可以同时接收一个元组,按位置赋给对应的变量(即解包赋值形式)。所以,函数返回多值其实就是返回一个元组,但写起来更方便。
这个例子是要求函数传入一个含有若干数据的列表(使用随机数),然后求这些数据的最大(使用max()函数)、最小(使用min()函数)和平均值并返回,因此返回的并不是一个数据,而是3个数,按上述的分析,只需要在函数的return语句后直接返回这3个数即可,相关实际代码设计如下:
import randomdef fun( li ): returnmax(li),min(li),sum(li)/len(li) # 求最大、最小和平均值并打包返回# 产生含10个随机数的列表li_nums = [random.randint(1,100) for i in range(10)]print(li_nums)Max, Min, avg = fun(li_nums) # 调用函数并将返回值(元组)解包print(f"最大值是{Max},最小值是{Min},平均值是{avg}。")
代码执行结果如下:
[82, 32, 83, 11, 34, 95, 81, 18, 71, 5]
最大值是95,最小值是5,平均值是51.2。