“MSE不就是一行代码的事?” 字节面试官:如果你不懂它背后的Hessian条件数和贝叶斯决策论,那你永远调不好超参数!

import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import TensorDataset, DataLoader
from sklearn.model_selection import train_test_split, KFold
import matplotlib.pyplot as plt

np.random.seed(42)
torch.manual_seed(42)

# 1) 数据
n = 600
x = np.random.uniform(-3.0, 3.0, size=(n, 1))

deff_true(x):
return0.5 * x**3 - 1.0 * x**2 + 2.0 * x + 3.0

sigma = 0.3 + 0.2 * np.abs(x)
y_true = f_true(x)
y = y_true + np.random.randn(n, 1) * sigma

# 划分训练/测试集
x_train, x_test, y_train, y_test, y_true_train, y_true_test = train_test_split(
    x, y, y_true, test_size=0.3, random_state=123
)

# 标准化 x 以改善高次多项式数值稳定性
x_mean, x_std = x_train.mean(), x_train.std()
defstandardize_x(x):
return (x - x_mean) / (x_std + 1e-12)

x_train_std = standardize_x(x_train)
x_test_std = standardize_x(x_test)

# 2) 多项式特征构造
defpoly_features(x, degree, include_bias=False):
# x: shape (n, 1)
# 返回 shape (n, degree) : [x^1, x^2, ..., x^degree]
    feats = [x**(d+1) for d in range(degree)]
    X = np.concatenate(feats, axis=1) if degree > 0else np.zeros((x.shape[0], 0))
if include_bias:
        X = np.concatenate([np.ones((x.shape[0], 1)), X], axis=1)
return X

# 3) PyTorch 模型定义（线性回归 on polynomial features）
classPolyReg(nn.Module):
def__init__(self, degree):
        super().__init__()
        self.linear = nn.Linear(degree, 1, bias=True)
defforward(self, X):
return self.linear(X)

# 4) 训练函数（返回训练好的模型与学习曲线）
deftrain_model_poly(x_train, y_train, x_val, y_val, degree=8, 
                     epochs=800, batch_size=64, lr=0.05, 
                     early_stop_patience=30, verbose=False, device='cpu'):
# 构建多项式特征
    Xtr = torch.tensor(poly_features(x_train, degree), dtype=torch.float32)
    Xva = torch.tensor(poly_features(x_val, degree), dtype=torch.float32)
    Ytr = torch.tensor(y_train, dtype=torch.float32)
    Yva = torch.tensor(y_val, dtype=torch.float32)

# 数据加载
    ds = TensorDataset(Xtr, Ytr)
    dl = DataLoader(ds, batch_size=batch_size, shuffle=True)

# 定义模型与优化器
    model = PolyReg(degree).to(device)
    criterion = nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)

    train_mse_hist = []
    val_mse_hist = []

    best_val = float('inf')
    best_state = None
    patience = 0

for epoch in range(epochs):
        model.train()
for xb, yb in dl:
            xb = xb.to(device)
            yb = yb.to(device)
            optimizer.zero_grad()
            pred = model(xb)
            loss = criterion(pred, yb)
            loss.backward()
            optimizer.step()

# 记录 train mse
        model.eval()
with torch.no_grad():
            train_pred = model(Xtr.to(device)).cpu()
            val_pred = model(Xva.to(device)).cpu()
            train_mse = criterion(train_pred, Ytr).item()
            val_mse = criterion(val_pred, Yva).item()
        train_mse_hist.append(train_mse)
        val_mse_hist.append(val_mse)

# 早停
if val_mse < best_val - 1e-8:
            best_val = val_mse
            best_state = {k: v.cpu().clone() for k, v in model.state_dict().items()}
            patience = 0
else:
            patience += 1
if patience >= early_stop_patience:
if verbose:
                    print(f"Early stopping at epoch {epoch+1}, best val MSE={best_val:.6f}")
break

# 加载最佳权重
if best_state isnotNone:
        model.load_state_dict(best_state)

return model, train_mse_hist, val_mse_hist

# 5) 训练/验证划分（再从训练集中切一部分出来作为验证集，用于早停）
x_tr_sub, x_val, y_tr_sub, y_val = train_test_split(
    x_train_std, y_train, test_size=0.25, random_state=321
)

# 选择一个代表性的 degree 用于主模型训练（例如 8）
main_degree = 8
model, tr_hist, va_hist = train_model_poly(
    x_tr_sub, y_tr_sub, x_val, y_val, 
    degree=main_degree, epochs=1200, lr=0.05, early_stop_patience=50, verbose=True
)

# 6) 主模型评估：在训练、测试集上计算 MSE
defpredict_model(model, x, degree):
    X = torch.tensor(poly_features(x, degree), dtype=torch.float32)
with torch.no_grad():
        yhat = model(X).cpu().numpy()
return yhat

yhat_train = predict_model(model, x_train_std, main_degree)
yhat_test = predict_model(model, x_test_std, main_degree)

mse_train = np.mean((yhat_train - y_train)**2)
mse_test = np.mean((yhat_test - y_test)**2)

print(f"Main model degree={main_degree}, Train MSE={mse_train:.6f}, Test MSE={mse_test:.6f}")

# 7) 自举法估计预测区间（快速 OLS 闭式解）
deffit_ols_closed_form(X, y):
# X: (n, p), y: (n, 1)
# 返回 w,b（我们以带偏置项作为第一列全1）
# 最小二乘解 (X^T X)^{-1} X^T y，使用 lstsq 提高稳健性
    w, *_ = np.linalg.lstsq(X, y, rcond=None)
return w

defpoly_with_bias(x, degree):
# 包含常数项
# 返回 [1, x, x^2, ..., x^degree]
    feats = [np.ones_like(x)]
    feats += [x**(d+1) for d in range(degree)]
return np.concatenate(feats, axis=1)

B = 120# bootstrap 轮数
grid = np.linspace(-3.2, 3.2, 400).reshape(-1, 1)
grid_std = standardize_x(grid)
X_boot = poly_with_bias(x_train_std, main_degree)
G_boot = poly_with_bias(grid_std, main_degree)

boot_preds = []
for b in range(B):
    idx = np.random.randint(0, X_boot.shape[0], size=X_boot.shape[0])
    Xb = X_boot[idx]
    yb = y_train[idx]
    wb = fit_ols_closed_form(Xb, yb)
    ygb = G_boot @ wb
    boot_preds.append(ygb.reshape(-1, 1))
boot_preds = np.concatenate(boot_preds, axis=1)  # (grid_n, B)
lower = np.percentile(boot_preds, 2.5, axis=1)
upper = np.percentile(boot_preds, 97.5, axis=1)

# 8) K 折验证：不同多项式次数下的 train/cv MSE
degrees = list(range(1, 13))
kf = KFold(n_splits=5, shuffle=True, random_state=777)

defcv_degree_mse(degree):
    train_mse_list, val_mse_list = [], []
for train_idx, val_idx in kf.split(x_train_std):
        xtr, xva = x_train_std[train_idx], x_train_std[val_idx]
        ytr, yva = y_train[train_idx], y_train[val_idx]
# 为加速，减少 epoch
        m, trh, vah = train_model_poly(
            xtr, ytr, xva, yva, degree=degree, 
            epochs=500, lr=0.05, early_stop_patience=25, verbose=False
        )
# 每折的最终模型在该折训练集上的 MSE 与验证集上的 MSE
        ytr_hat = predict_model(m, xtr, degree)
        yva_hat = predict_model(m, xva, degree)
        train_mse_list.append(np.mean((ytr_hat - ytr)**2))
        val_mse_list.append(np.mean((yva_hat - yva)**2))
return np.mean(train_mse_list), np.std(train_mse_list), np.mean(val_mse_list), np.std(val_mse_list)

cv_results = []
for deg in degrees:
    tr_m, tr_s, va_m, va_s = cv_degree_mse(deg)
    cv_results.append((deg, tr_m, tr_s, va_m, va_s))
    print(f"Degree={deg:2d} | Train MSE={tr_m:.4f}±{tr_s:.4f} | Val MSE={va_m:.4f}±{va_s:.4f}")

# 找一个 cv 最优的复杂度
val_mse_means = [it[3] for it in cv_results]
best_deg = degrees[int(np.argmin(val_mse_means))]
print(f"Best degree by CV: {best_deg}")

# 9) 可视化 - 分开展示四个图

# 图1：数据与拟合曲线、真实函数、预测区间
plt.figure(figsize=(10, 8))
plt.scatter(x_train, y_train, s=18, c='#1E90FF', alpha=0.6, label='Train')
plt.scatter(x_test, y_test, s=18, c='#FF8C00', alpha=0.6, label='Test')
plt.plot(grid, f_true(grid), color='#00FF00', linewidth=3.0, label='True f(x)')
# 主模型预测曲线
y_grid_pred = predict_model(model, grid_std, main_degree)
plt.plot(grid, y_grid_pred, color='#FF00FF', linewidth=3.0, label=f'Pred (deg={main_degree})')
# 预测区间
plt.fill_between(grid.ravel(), lower.ravel(), upper.ravel(), color='#00FFFF', alpha=0.25, label='Bootstrap 95% PI')
plt.title('数据、真实函数、模型预测与预测区间', fontweight='bold', fontsize=16)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.legend(loc='best', fontsize=10)
plt.grid(alpha=0.25)
plt.tight_layout()
plt.show()

# 图2：残差-拟合值图（Residuals vs Fitted）
plt.figure(figsize=(10, 8))
# 使用测试集残差诊断泛化误差
y_test_pred = yhat_test
resid = (y_test - y_test_pred).ravel()
fitted = y_test_pred.ravel()
cmap = plt.get_cmap('turbo')
norm = plt.Normalize(vmin=np.min(np.abs(resid)), vmax=np.max(np.abs(resid)))
colors = cmap(norm(np.abs(resid)))
plt.scatter(fitted, resid, c=colors, s=28, alpha=0.9, edgecolor='k', linewidth=0.2)
plt.axhline(0.0, color='black', linestyle='--', linewidth=1.2)
# 画分箱后的趋势线
bins = np.linspace(fitted.min(), fitted.max(), 18)
idxs = np.digitize(fitted, bins)
bin_centers = []
bin_means = []
for b in range(1, len(bins)+1):
    mask = (idxs == b)
if np.sum(mask) > 4:
        bin_centers.append(np.mean(fitted[mask]))
        bin_means.append(np.mean(resid[mask]))
if len(bin_centers) > 1:
    plt.plot(bin_centers, bin_means, color='#FF1493', linewidth=2.5, label='Binned trend')
plt.title('残差-拟合值图（颜色=|残差|）', fontweight='bold', fontsize=16)
plt.xlabel('Fitted values', fontsize=12)
plt.ylabel('Residuals', fontsize=12)
plt.legend(loc='best', fontsize=10)
plt.grid(alpha=0.25)
plt.tight_layout()
plt.show()

# 图3：学习曲线（训练/验证 MSE 随 epoch 的变化）
plt.figure(figsize=(10, 8))
plt.plot(np.arange(1, len(tr_hist)+1), tr_hist, color='#FF0000', linewidth=2.2, label='Train MSE')
plt.plot(np.arange(1, len(va_hist)+1), va_hist, color='#32CD32', linewidth=2.2, label='Val MSE')
plt.title('学习曲线（早停）', fontweight='bold', fontsize=16)
plt.xlabel('Epoch', fontsize=12)
plt.ylabel('MSE', fontsize=12)
plt.legend(loc='best', fontsize=10)
plt.grid(alpha=0.25)
plt.tight_layout()
plt.show()

# 图4：模型复杂度曲线（K 折 CV）
plt.figure(figsize=(10, 8))
tr_means = [it[1] for it in cv_results]
tr_stds  = [it[2] for it in cv_results]
va_means = [it[3] for it in cv_results]
va_stds  = [it[4] for it in cv_results]
plt.errorbar(degrees, tr_means, yerr=tr_stds, fmt='-o', color='#00BFFF', linewidth=2.2, capsize=4, label='Train MSE (mean±std)')
plt.errorbar(degrees, va_means, yerr=va_stds, fmt='-s', color='#FFA500', linewidth=2.2, capsize=4, label='CV MSE (mean±std)')  
plt.axvline(best_deg, color='#9400D3', linestyle='--', linewidth=2.0, label=f'Best deg={best_deg}')
plt.title('模型复杂度选择（K 折交叉验证）', fontweight='bold', fontsize=16)
plt.xlabel('Polynomial degree', fontsize=12)
plt.ylabel('MSE', fontsize=12)
plt.legend(loc='best', fontsize=10)
plt.grid(alpha=0.25)
plt.tight_layout()
plt.show()

数据、真实函数、模型预测与预测区间：

蓝色散点（训练）、橙色散点（测试）展示样本与噪声强度随 x 增大而增加（异方差性）。

绿色曲线为真实函数。品红色曲线是我们训练的多项式回归预测曲线。青色半透明带为自举法估计的 95% 预测区间。

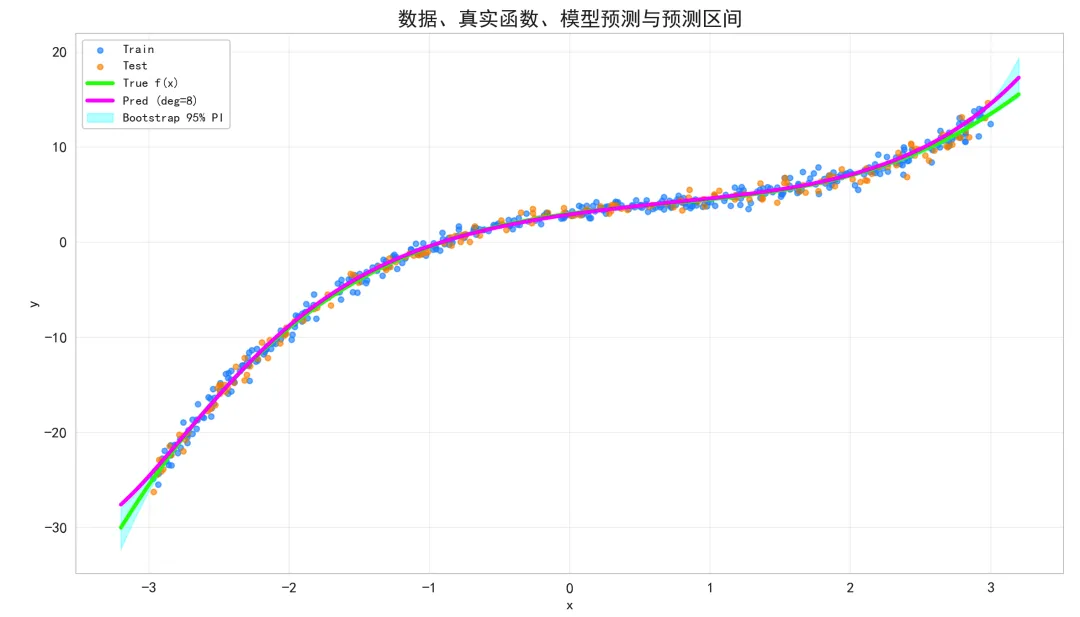
• 如果预测曲线贴近真实曲线，说明偏差小。
• 预测区间宽度随 x 变化反映不确定性与数据密度差异；若带宽在某些区域明显更宽，说明这些区域模型方差更大或数据稀疏。
• 测试点与预测区间对齐良好，表明模型泛化尚可。

残差-拟合值图：

横轴为模型拟合值，纵轴为残差。

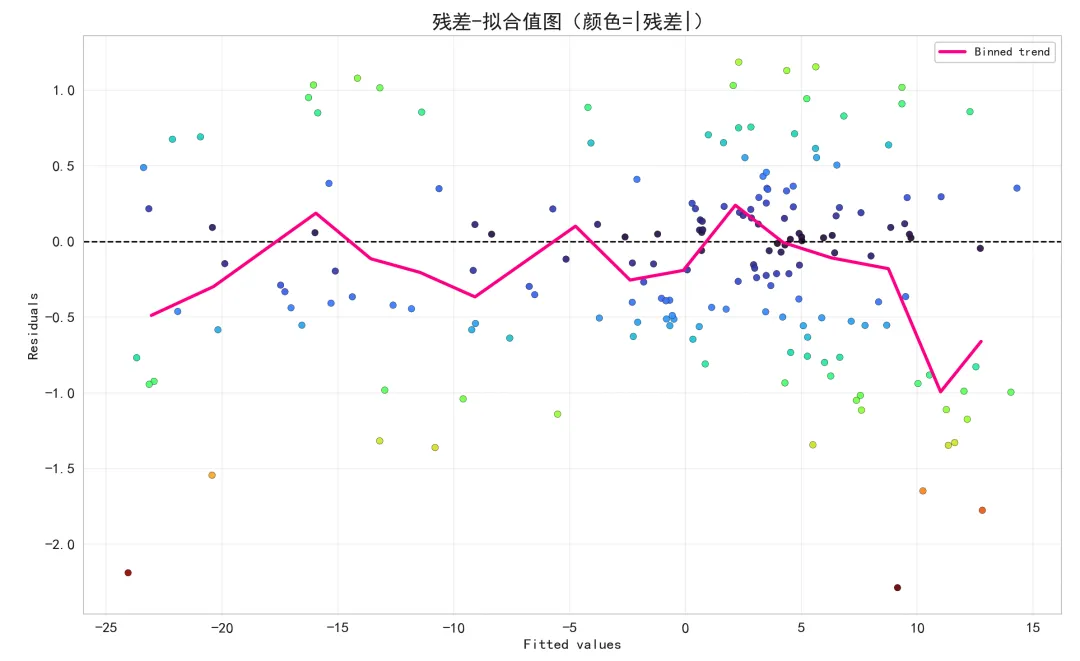
若点云均匀围绕 0 且无系统结构，说明线性可加性假设较合理；若存在锥形或弧形结构，提示异方差或模型偏差。

我们的合成数据是异方差噪声，因此可以预期在拟合值较大或较小的区域残差散布更宽。Binned trend 曲线若系统偏离 0，说明模型结构有偏差（例如多项式阶数不足或过度正则）。

学习曲线：

红色为训练集 MSE，绿色为验证集 MSE。

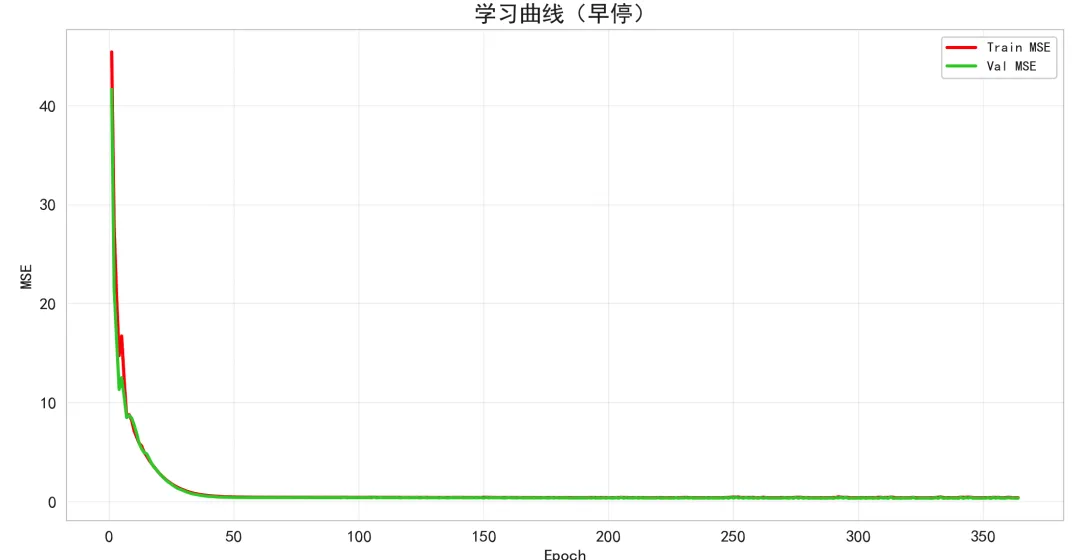
典型现象：开始阶段二者均下降；若后期训练误差继续下降而验证误差回升，表明过拟合；早停点通常选择验证误差最低处。

由于我们使用了早停，最终模型权重落在验证误差最优点附近，避免了过拟合。

模型复杂度选择：

横轴为多项式次数，纵轴为 MSE。蓝线为训练 MSE（含标准差），橙线为 5 折 CV 验证 MSE（含标准差）。

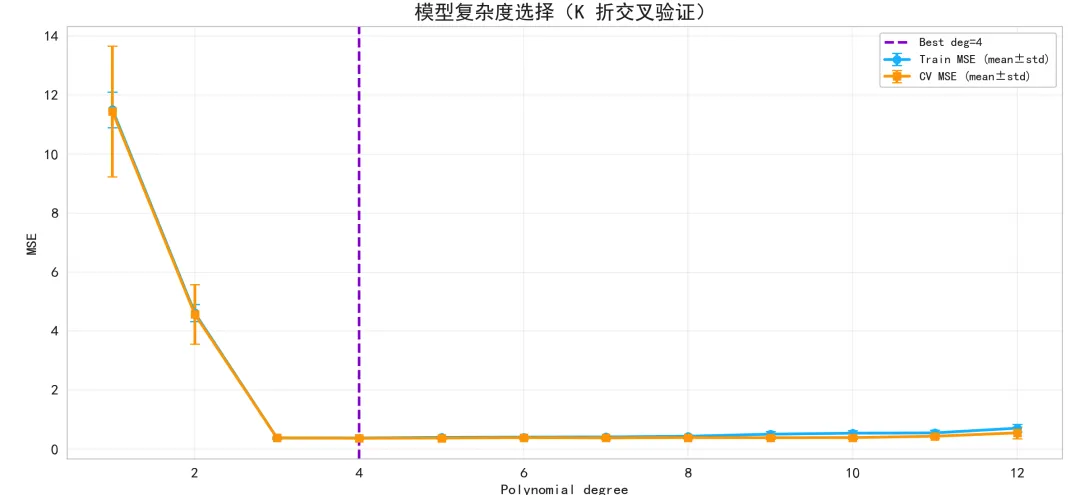
经典 U 型曲线：低次数下偏差大（验证误差高），高次数下方差大（验证误差又升高）；某个中间次数对应验证误差最低，标为最佳次数。

如果最佳次数与主模型选择一致或接近，说明我们的复杂度设定合理。

结论

理论上，MSE 在高斯同方差假设下与最大似然一致，是最自然、解析性最好的回归损失。

实践中，MSE 对异常值与异方差敏感，需要：在建模前进行数据清洗与异常值诊断；复杂度或加入正则/早停；使用 K 折交叉验证选择复杂度等等。

最后