超透镜作为超表面在平面成像与光场调控领域的重要应用形式，因其超薄结构与灵活的相位调控能力而受到广泛关注。然而，受材料色散与结构色散的共同影响，传统超透镜通常仅能在窄带波长范围内实现理想聚焦，色差问题严重制约了其在宽带成像与显示系统中的应用。本期内容将围绕宽带消色差超透镜的设计需求，构建了一套从 Python / MATLAB 数值建模到 FDTD 仿真的完整设计流程。通过引入粒子群优化（Particle Swarm Optimization, PSO）算法，对超表面单元结构参数进行全局搜索与优化，在多个工作波长下实现透射相位的协同匹配，从而有效抑制焦距漂移并提升宽带聚焦性能。
Wang, S., Wu, P.C., Su, VC. et al. Broadband achromatic optical metasurface devices. Nat Commun 8, 187 (2017). https://doi.org/10.1038/s41467-017-00166-7
https://www.nature.com/articles/s41467-017-00166-7#citeas
根据上述文献所说，要实现宽带消色差超透镜，必须在宽波长范围内提供焦距保持不变的相位延迟，对于工作波长在λ∈(λmin，λmax)的情况，聚焦超透镜的相位分布可以表示为：
其中：
因此，只有同时满足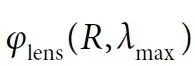
和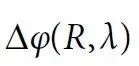
这两个相位特性，才能实现宽带消色差的功能。其中，前者表现出与波长无关的调制，它仅仅与λmax有关而独立于工作波长λ，利用几何相位就可以获得相应的相位分布，并且这种相位调制机制只依赖于单元结构的旋向或半径变化。相反，后者Δφ(R, λ)是一个与工作波长相关的函数，并与1/λ 存在一种线性关系。它代表了不同入射波长之间的相位差，如图1(b)所示。该相位差可以通过设计每个单元结构的传输相位响应来补偿，当然单元结构的相位响应也应与1/λ成线性关系。由于传输相位响应机理与几何相位的不同，因此通过合适的设计两者可不互相干扰，并可以把它们简单地合并在一起。然而，并不是每个单元结构的传输相位均与1/λ 成线性关系，因此可以引入一个额外的相位因子C(λ)，通过优化设计去实现特定波长的相位补偿。值得注意的是，这样的相移并不会影响超透镜的聚焦特性，如图1 所示。在此基础上，可以将消色差超透镜的相位剖面改写为：其中C(λ)是一个由优化算法得到的仅与波长相关的相位因子。
二、Step 2｜单元结构设计
设计模型的基本单元结构，和前面几期一样，这里不再做详细赘述了。如下：
随后通过扫参和优化得到尺寸和透射率以及尺寸和相位的数据库。
三、Step 3｜粒子群优化算法（PSO)--python/matlab
超透镜所产生的实际相位波面难以与理想相位波面实现完全匹配。二者之间的偏差可通过引入补偿函数 C(λ)C(\lambda)C(λ) 进行描述，并进一步转化为一个以误差最小化为目标的优化问题。针对该类极值问题，已有多种求解方法被广泛研究与应用，如遗传算法、模拟退火算法以及蚁群算法等。在粒子群优化（Particle Swarm Optimization，PSO）算法中，每个粒子由三维向量构成，分别表示粒子的当前位置 xix_ixi、历史最优位置 pip_ipi 以及飞行速度 viv_ivi。在优化迭代过程中，粒子的速度与位置更新关系可表示为：
其中，rand表示在区间 (0,1)内生成的随机数，w为惯性权重因子，c1和 c2为加速因子（经验取值），pgbest表示全局最优适应度对应的位置。项 c1×rand×(pi−xi)反映了粒子对自身历史最优解的学习能力，而 c2×rand×(pgbest−xi)则体现了粒子之间的信息共享与协同搜索机制。在本文中，C(λ)被定义为粒子的位置信息向量 xi，用于对不同波长下的相位误差进行补偿，并将理想相位波面与实际相位波面之间的差异作为适应度函数，从而实现超透镜相位调控性能的优化，因此通过设计PSO算法不断迭代得到最优的参数值。
四、Step 4｜根据PSO得到的位置参数建立透镜模型
五、Step 5｜计算聚焦光斑
根据步骤四宽带消色差超透镜结构建议相应光源，在FDTD中编写代码实现不同波长下的远场聚焦效果如下，可以看到不同波长(1000 nm、1150 nm、1200 nm、1250 nm)下光斑的聚焦中心几乎聚焦在同一位置。
