1. 为什么在双容水箱系统中弃用传统 PID?
在工业工程控制应用中,双容水箱是一个典型的二阶耦合控制对象。其动力学行为遵循以下公式:
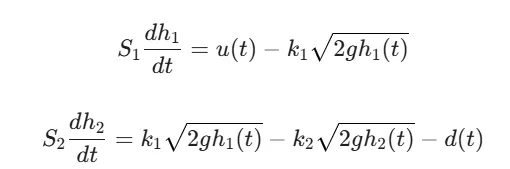 其中:
其中:如果选用传统 PID,通常会有两个难以逾越的问题需要面对:
- 1. 约束冲突:PID控制很难在不触碰进水泵流量饱和(Saturation)和液位溢出保护两个约束的前提下实现最优的动态响应。
- 2. 模型失配与稳态误差:相较于真实的物理特性(Plant),系统的线性化模型往往存在天然偏差。在面对负载扰动时,标准的 MPC 往往无法彻底消除静差。
下面文章将展示如何通过 状态增广(State Augmentation) 方法去实现无静差(Offset-Free)MPC模型的构建。其核心思路是在状态空间中显式引入误差积分项,利用滚动优化(Receding Horizon)在约束范围内寻找全局最优解。
2. 物理仿真环境:非线性 Plant 模拟
在设计控制器之前,我们首先需要去构建一个高仿真的模拟系统。代码直接在连续动力学的方程上进行内容修改,添加了针对传感器自身的噪声和相关阶跃扰动信号。
def tank_physics_step(h, u, dt, noise_std=0.005, leak_disturb=0.0): """ 双容水箱非线性动力学演化 微分方程:S * (dh/dt) = Q_in - Q_out """ u_val = float(np.asarray(u).flatten()[0]) h = np.asarray(h).flatten() # 结构参数:截面积 S, 流量系数 k S1, S2 = 0.5, 0.5 k1, k2 = 0.2, 0.15 g = 9.81 # 处理液位非负的物理边界 h1_safe, h2_safe = max(h[0], 1e-6), max(h[1], 1e-6) # 基于伯努利原理的非线性流量计算 flow_1_to_2 = k1 * np.sqrt(2 * g * h1_safe) flow_out_2 = k2 * np.sqrt(2 * g * h2_safe) # 离散化演化 dh1 = (u_val - flow_1_to_2) / S1 dh2 = (flow_1_to_2 - flow_out_2 - leak_disturb) / S2 h_next = h + np.array([dh1, dh2]) * dt # 模拟真实工业传感器的测量噪声 measured_h = h_next + np.random.normal(0, noise_std, size=2) return h_next, np.maximum(measured_h, 0)
设计要点:
- • 其中
np.sqrt 体现出系统具备强非线性的特点。 - • 通过设计
leak_disturb来模拟整个系统中的weizhi的泄露流量。
3. Offset-Free 控制器:从线性化到状态增广
3.1 增广状态空间的设计逻辑
在面对常值扰动的时候,传统的MPC系统往往表现不佳。我们可以通过引入跟踪误差的积分项来解决这一问题。增广后的系统定义如下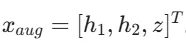
class OffsetFreeMPC: def __init__(self, Ad, Bd, Np, Nc, Q, R, Rd, h_max, u_max, du_max): # 增广矩阵构建:将误差积分 z(k+1) = z(k) + (h2(k) - r) 转化为状态空间表达 C = np.array([[0, 1]]) # 输出观测矩阵 self.A_aug = np.block([ [Ad, np.zeros((2, 1))], [C @ Ad, np.eye(1)] ]) self.B_aug = np.vstack([Bd, C @ Bd]) # 求解离散黎卡提方程 (DARE),获得终端惩罚矩阵 P 以确保稳定性 P = solve_discrete_are(Ad, Bd, Q[:2, :2], R) self.P_terminal = np.zeros((3, 3)) self.P_terminal[:2, :2] = P
核心解读:
- • 稳定性判据:通过计算终端代价P,我们为控制器提供了一个“软着陆”的预测目标,其存在目的提升控制器的收敛性能。
3.2 滚动时域下的二次规划 (QP) 求解
我们使用 CVXPY 构建优化问题。控制目标不仅是液位跟踪,还要兼顾控制量的平滑。
def solve(self, x0_meas, z0, ref, u_last, dt=0.5, t_curr=0): # 决策变量:控制增量序列 du (Incremental Control) du = cp.Variable((self.B_aug.shape[1], self.Nc)) x = cp.Variable((self.A_aug.shape[0], self.Np + 1)) # 初始状态与目标配置 [h1=0, h2=ref, z=0] x0_aug = np.hstack([x0_meas.flatten(), z0]) ref_aug = np.array([0, ref, 0]) constraints = [x[:, 0] == x0_aug] cost = 0 for k in range(self.Np): # 处理控制时域约束 if k < self.Nc: u_k = u_last + cp.sum(du[:, :k + 1], axis=1) constraints += [ du[:, k] <= self.du_max, du[:, k] >= -self.du_max, # 变化率限制 u_k >= 0, u_k <= self.u_max # 执行器硬约束 ] cost += cp.quad_form(du[:, k], self.Rd) + cp.quad_form(u_k, self.R) else: u_k = u_last + cp.sum(du[:, :], axis=1) # 动力学预测与状态权重惩罚 constraints += [x[:, k + 1] == self.A_aug @ x[:, k] + self.B_aug @ u_k] cost += cp.quad_form(x[:, k + 1] - ref_aug, self.Q) # 最终代价叠加 cost += cp.quad_form(x[:, self.Np] - ref_aug, self.P_terminal) # 调用 OSQP 求解器 prob = cp.Problem(cp.Minimize(cost), constraints) prob.solve(solver=cp.OSQP, warm_start=True) # 取最优动作序列的第一步执行 new_u = np.clip(float(u_last) + float(du[:, 0].value), 0, self.u_max) z_next = z0 + dt * (x0_meas[1] - ref) # 显式积分更新 return new_u, z_next, self.predict_future(x0_meas, new_u, dt, t_curr)
关键细节解析:
- • 增量式 MPC:和传统工业一致,我们通过优化△u,来对阀门的开启速度进行物理限制。
- • 暖启动 (Warm Start):可以通过设置参数量
warm_start=True,利用上一时刻的值来计算当前的收敛计算。
4. 仿真表现定量分析
在300 步的仿真中,系统展现出如下特性:
- 1. 稳态追踪:系统在经历初始调节后,Tank 2 的液位能够以极小的超调量稳定在 1.2m。
- 2. 抗扰动能力:在第 70 步注入外部泄露扰动d=0.05后,液位出现瞬态波动。此时增广状态中的积分项迅速介入,控制器自动增加了进水流量 。即使在线性化模型不完全准确的情况下,系统仍能在 30 步内重新消除稳态误差。
- 3. 约束一致性:无论是在启动阶段还是扰动恢复阶段,控制量u始终被严格限制在范围内,体现了 MPC 在显式处理约束方面的压倒性优势。
全部代码请前往CSDN学而要时习获取