Python基础篇 - 函数的递归(Recursion)
- 2026-02-10 13:44:19
Python基础篇 - 函数的递归(Recursion)
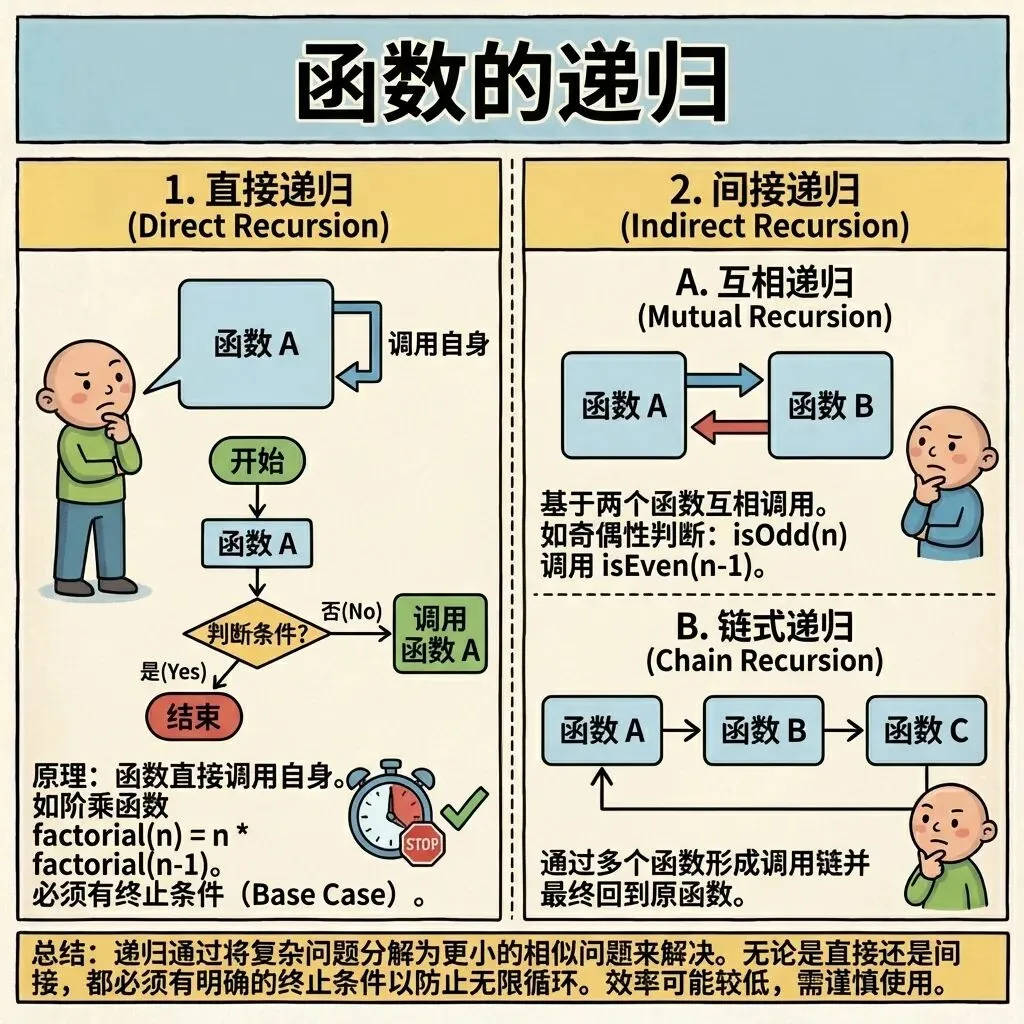
函数的递归 







<合集链接> 这里是我滴合集内容链接,大家感兴趣就康康吧。 1. 人工智能进阶之路 - 机器学习篇 2. Origin-study 3. 人工智能进阶之路-Python基础篇 4. 充电er的乱坠闲聊(我自己的日常生活篇) 5. Origin认知 
点个 赞 你最好看



今天的基础篇内容讲解函数的递归的基本知识,大家这么聪明,一看就会了。
1. 递归:递归一种是逻辑思想,将一个大工作分为逐渐减小的小工作,只不过在程序中,是依靠函数嵌套这个特性来实现了。
2. 递归的本质:函数嵌套,在函数体中调用自身函数,直到函数满足出口条件(递归结束的条件)。
3. 应用场景:高效地解决具有重复子问题特征的问题,逐步拆分,然后一层层的反向返回结果。
函数递归代码示例:
# 示例:计算n的阶乘(n!)# 1.非递归实现(循环迭代)def factorial_iterative(n):"""非递归(循环)计算阶乘"""result = 1 # 初始值:0!和 1!都为1# 从2到n累乘for i in range(2, n + 1):result *= ireturn result# 2.递归实现def factorial_recursive(n):"""递归计算阶乘"""# 递归终止条件(必须要有终止条件,否则无限递归)if n == 0 or n == 1:return 1# 递归调用:n! = n × (n-1)!return n * factorial_recursive(n - 1)




总结:今日我们学习了Python基础篇-函数的递归(Recursion):函数的递归,核心是理解递归 “自我调用、逐步拆解” 的本质:以阶乘为例,递归解法通过明确的终止条件(n=0/1: 返回1),将大问题拆分为更小的子问题,直到触达终止条件后反向返回结果(先拆分、再一层层反向返回结果)。对比非递归的循环累乘,递归代码更简洁、贴合数学逻辑,但必须注意终止条件的设置,否则会引发无限递归。递归是编程中重要的思维方式,掌握它能更高效地解决具有重复子问题特征的问题。在Python基础篇,后续我们将持续学习Python基础知识,祝每一位study er学习愉快。





本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。
