Python 模拟布朗运动
- 2026-01-22 17:36:42
在本文中,我们将探讨布朗运动(Brownian Motion)的模拟方法——这是衍生品定价中最基础的概念之一。布朗运动是一种数学模型,用于模拟资产价格的行为,从而为期权合约的定价提供依据。
对某项资产上的期权进行定价的一种典型方法是:在期权存续期内,模拟大量随机的资产价格路径;在每条路径下计算该期权的收益;然后对所有路径下的期权价格取平均值,并将该平均值折现,从而得到最终的期权价格。这正是蒙特卡洛(Monte Carlo)方法的一个典型应用。
本文将专注于使用 Python 编程语言模拟布朗运动路径。我们将首先介绍“标准布朗运动”(Standard Brownian Motion),随后逐步增加布朗运动动态的复杂性。与 QuantStart 网站的所有文章一样,本文将提供完整的代码,以便读者能够完全复现下文所示的结果。
本文深受 Paul Glasserman 所著的《金融工程中的蒙特卡洛方法》(Monte Carlo Methods for Financial Engineering)[Glasserman, 2003] 一书的影响。该书详细阐述了相关理论基础,导出了下文所使用的离散化公式(本文将直接给出这些公式,而不进行推导)。
文章首先模拟所谓的“标准布朗运动”,即均值为零、方差为单位1的布朗运动路径。接着,我们将讨论如何在模拟中引入非零常数均值和非常数(但为常量)方差。在后续文章中,我们将进一步探讨均值和方差随时间变化的情形:首先考虑分段常数的均值与方差,之后再扩展到完全随时间变化的均值与方差情形。
注:如果您希望回顾布朗运动的数学定义,请参阅我们此前发表的相关文章。
标准布朗运动
以下公式引自 [Glasserman, 2003] 一书中的公式 (3.2)。该公式给出了在 n 个时间点(时间点不一定等间距)上生成一条(单条)布朗运动路径的递推关系。其核心含义是:在时刻 ti 的新布朗运动路径值,等于前一时刻 ti−1 的路径值,加上时间间隔 Δti=ti−ti−1 的平方根与一个在时刻 ti 生成的标准正态分布随机样本的乘积。
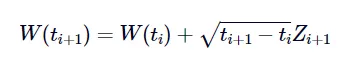
然而,我们将利用 Python 的 NumPy 库所提供的向量化方法,同时生成 N 条路径。为此,我们将从标准正态分布中一次性抽取 N 个随机样本,然后利用上述递推关系,在向量化操作中并行地模拟这 N 条路径。
首先,我们需要导入后续分析所需的相关量化计算与可视化库,包括 Matplotlib、NumPy、Pandas 和 Seaborn:
import matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport seaborn as sns
我们还需要设置一个随机种子值,以确保您生成的结果与我们的完全一致。为此,我们需要使用一个(伪)随机数生成器(RNG),此处使用的是 NumPy 提供的默认生成器。接着,必须提供一个整数作为种子值,以确保以下所有结果均可复现:
rng = np.random.default_rng(42)paths = 50points = 1000
mu, sigma = 0.0, 1.0Z = rng.normal(mu, sigma, (paths, points))interval = [0.0, 1.0]dt = (interval[1] - interval[0]) / (points - 1)
t_axis = np.linspace(interval[0], interval[1], points)W[:, real_idx]),将每条路径在该时刻的值设为前一时刻的值,加上时间步长 Δt 的平方根与矩阵 Z 中对应的标准正态随机样本的乘积:W = np.zeros((paths, points))for idx in range(points - 1):real_idx = idx + 1W[:, real_idx] = W[:, real_idx - 1] + np.sqrt(dt) * Z[:, idx]
subplots 方法,它能让我们更精细地控制图形和坐标轴的配置。我们指定创建一个单行单列的子图,并以英寸为单位设置图形尺寸(默认分辨率为 100 dpi)。随后,我们遍历所有路径,将时间轴与矩阵 W 中对应的每一行(使用 NumPy 的向量化语法 W[path, :])进行绘图。最后,显示该图形:fig, ax = plt.subplots(1, 1, figsize=(12, 8))for path in range(paths):ax.plot(t_axis, W[path, :])ax.set_title("Standard Brownian Motion sample paths")ax.set_xlabel("Time")ax.set_ylabel("Asset Value")plt.show()
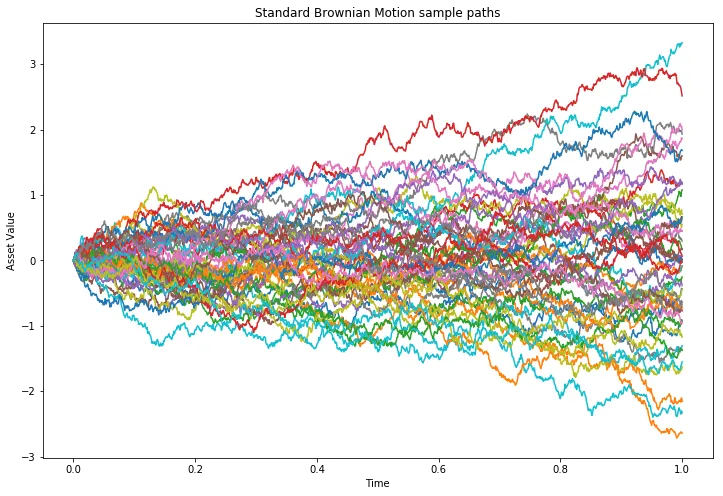
可以明显看出,在接近 T(模拟结束时刻)时,大部分路径的取值集中在零附近,落在 [−1,1] 区间内,而少数路径则表现出更极端的终值。这正是标准布朗运动所预期的行为。
然而,我们可以通过对所生成的 N 条样本路径的终值分布进行量化分析,使这一观察更加严谨。为此,我们可以使用核密度估计(Kernel Density Estimate, KDE),这是一种从有限样本数据中估计连续概率分布的方法。我们将使用 Seaborn 统计可视化库来实现这一点。
第一步是创建一个 Pandas DataFrame(包含单列),其中存储所有样本路径在终点时刻的取值:
final_values = pd.DataFrame({'final_values': W[:, -1]})fig, ax = plt.subplots(1, 1, figsize=(12, 8))sns.kdeplot(data=final_values, x='final_values', fill=True, ax=ax)ax.set_title("Kernel Density Estimate of asset path final value distribution")ax.set_ylim(0.0, 0.325)ax.set_xlabel('Final Values of Asset Paths')plt.show()
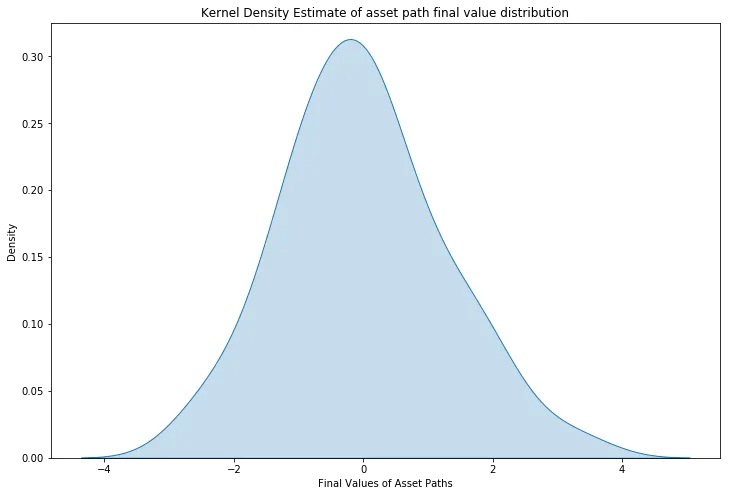
print(final_values.mean(), final_values.std())(final_values -0.011699dtype: float64,final_values 1.251382dtype: float64)
所得均值为 -0.01,接近于零;标准差为 1.25,也相当接近于 1。如果模拟的路径数量进一步增加,根据大数定律,这些统计量将趋近于标准正态分布的理论值(即均值为 0,标准差为 1)。
在下一节中,我们将允许采样路径具有非零均值和非单位标准差。
具有常数漂移率与波动率的布朗运动
下一个递推关系式引自 [Glasserman, 2003] 中的公式 (3.3)。它是对前述公式的改进,在原有基础上增加了一项 μΔt,并将最后一项乘以 σ。正是这两个修改使得布朗运动路径可以具有非零均值(由 μ 控制)和非单位标准差(由 σ 控制):
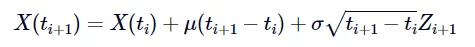
mu_c, sigma_c = 5.0, 2.0mu_c * dt 项,并在后一项中加入了 sigma_c * ...。由于我们仍然使用固定长度的时间步长,因此依然可以使用常量 Δt(即 dt):X = np.zeros((paths, points))for idx in range(points - 1):real_idx = idx + 1X[:, real_idx] = X[:, real_idx - 1] + mu_c * dt + sigma_c * np.sqrt(dt) * Z[:, idx]
fig, ax = plt.subplots(1, 1, figsize=(12, 8))for path in range(paths):ax.plot(t_axis, X[path, :])ax.set_title("Constant mean and standard deviation Brownian Motion sample paths")ax.set_xlabel("Time")ax.set_ylabel("Asset Value")plt.show()
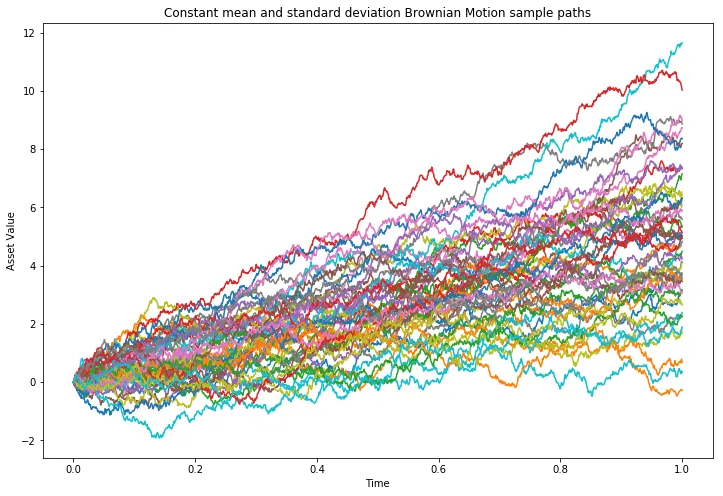
注意这些路径呈现出向均值 5 的正向漂移趋势,且其离散程度(波动幅度)相比标准布朗运动明显增大。通过调整 μc 和 σc 的取值,也可以生成具有不同动态特征的路径。
下一步计划
在本系列的下一篇文章中,我们将放宽均值和标准差为常数的假设,转而引入随时间变化的均值和标准差,以构建更复杂的资产价格动态模型。在后续文章中,我们还将探讨多维布朗运动、“布朗桥”(Brownian Bridge)以及几何布朗运动(Geometric Brownian Motion)。
