内附代码|交叉滞后模型怎么选?JRP主编示范:用RI-CLPM探究双向因果

在心理学纵向研究中，我们经常需要探讨变量A与B之间“谁预测谁”的问题。

这个时候，我们都会习惯性先跑一下交叉滞后面板模型（CLPM）。

但在阅读文献或面对审稿意见时，我们不难发现：现在单纯使用CLPM经常会受到质疑。

顶级心理学期刊Journal of Research in Personality主编Richard E. Lucas曾指出，CLPM的局限在于它未能区分“个体间差异”与“个体内变异”。

如果不能有效剥离个体稳定的特质水平，CLPM捕捉到的结果很可能具有误导性。

为此，随机截距交叉滞后面板模型（RI-CLPM）提供了一种更稳健的方案。

它的核心逻辑是通过提取随机截距，排除个体自身稳定水平的干扰，从而更精准地捕捉变量间的动态因果效应。

本文将解读作者Lucas发表在Journal of Personality（2024年影响因子2.7，JCR Q2区）上的研究。

探讨Lucas建议从CLPM转向RI-CLPM的原因，并详细解析其公开的R语言代码，方便大家在实际研究中参考使用。

文章来源：Lucas, R. E., & Rohrer, J. M. (2024). On the robustness of reciprocal associations between personality and religiosity in a German sample. Journal of Personality, 92(6), 1649-1667. https://doi.org/10.1111/jopy.12964

Lucas这篇文章，其实是对Entringer等人（2023）关于“大五人格与宗教关系”研究的一次硬核复核。

他认为原研究使用CLPM模型不够科学，结论可能不稳健。

于是用RI-CLPM重新跑了遍数据，直接用实证结果进行了反驳。

在看Lucas的反驳之前，先快速同步一下原研究到底做了什么：

Entringer等人追踪了4万多名德国被试，时间跨度长达12年（共4波纵向数据）。

他们主要想探讨大五人格和宗教之间是否存在双向因果？

以及这种关系是否会受到地区（文化）的调节？

测量工具：大五人格（每个特质3道题）和宗教（参与宗教活动的频率，1道题）。

原研究结论：大五人格和宗教之间确实存在双向预测效应，且这种效应受地区调节。

原研究来源：Entringer, T. M., Gebauer, J. E., & Kroeger, H. (2023). Big five personality and religiosity: Bidirectional cross-lagged effects and their moderation by culture. Journal of Personality, 91(3), 736–752. https://doi.org/10.1111/jopy.12770

在本文中，Lucas对原研究结果的稳健性提出了一系列质疑。

模型选择

原研究使用的是传统交叉滞后面板模型（CLPM）。

简单来说，这个模型的逻辑是在控制了变量Y原有的水平（前一波的Y）后，看前一波的变量X还能不能预测后一波Y的变化。

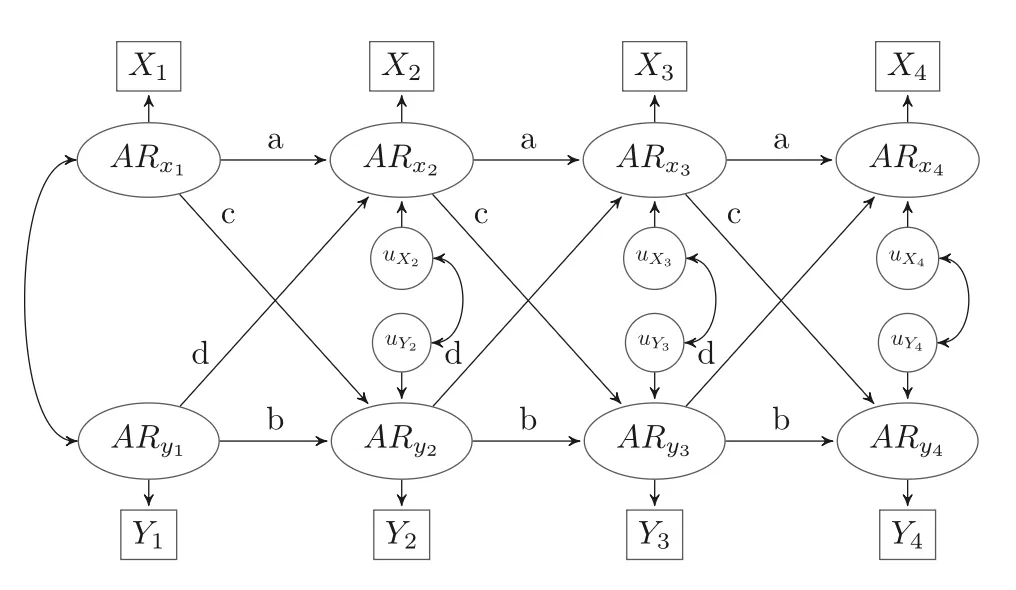
CLPM路径图

但Lucas的质疑就在这里：

CLPM有一个核心假设，它认为除了变量自身的稳定性（自回归效应）和跨时间的相互影响（滞后效应）外，就没有其他稳定性来源了。

这恰恰与心理学研究的常识相违背。

因为心理学研究的大多数变量（比如人格、宗教）往往自带一种“稳定的底色”——也就是个体间稳定的特质差异。

CLPM的问题在于把这种“天生的稳定差异”和“随时间产生的动态变化”混在了一起。

Lucas指出，在某些现实情境下，这种模型设定错误会100%出现虚假的滞后效应。

打个比方：假如我们在研究小朋友的“饭量”和“体重”之间的关系。

小明小朋友天生块头大、基础代谢高，这是他自身的稳定特质，所以他自然吃得比别人多，体重也比别人重。

在CLPM的视角下：模型看到小明第一年饭量大，第二年体重重，就很容易得出“饭量显著预测了体重增长”的结论。

但实际情况是：这仅仅是因为小明本身“块头大”这一稳定特质在起作用，并不是因为他多吃那口饭导致了体重的动态增长。

这就是Lucas质疑的点：如果不把这种“稳定的底色”剥离出来，我们所看到的双向因果，很可能只是一种统计错觉。

变量控制

其次，原研究将大五人格的五个特质同时放入模型去预测宗教，但这忽略了在现实情境中，各个特质之间并非完全独立。

因为模型同时纳入并控制了所有特质，统计上最后评估的其实是剔除共有变异后的“数学残差”，而不再是原本心理学意义上的特质了。

比如： 我们把“苹果”和“梨”同时放进模型分析。

因为它们都是水果，都有果皮、果核和果肉，模型会把这些共有的部分全部剔除掉，只针对它们剩下的不同点进行分析。

但问题是，这些剩下的“残差”真的还能代表苹果或梨本身吗？

此外，一次性纳入所有大五人格特质会增加模型的复杂度，进而可能干扰参数估计的准确性。

效应量

最后，原研究得出的交叉滞后效应量其实非常小。

Lucas指出，研究者需要解释为什么这么微小的效应具有重要意义。

而且，极小的效应量往往可能只是由微小的模型设定错误，或者某些残留的混淆因素引起的偏差，并不一定代表真实存在的因果关系。

质疑过后，Lucas直接上手对原数据重新进行了建模，以此来反驳原研究结果的稳健性。

具体的操作和结果，我们可以看下面几个维度。

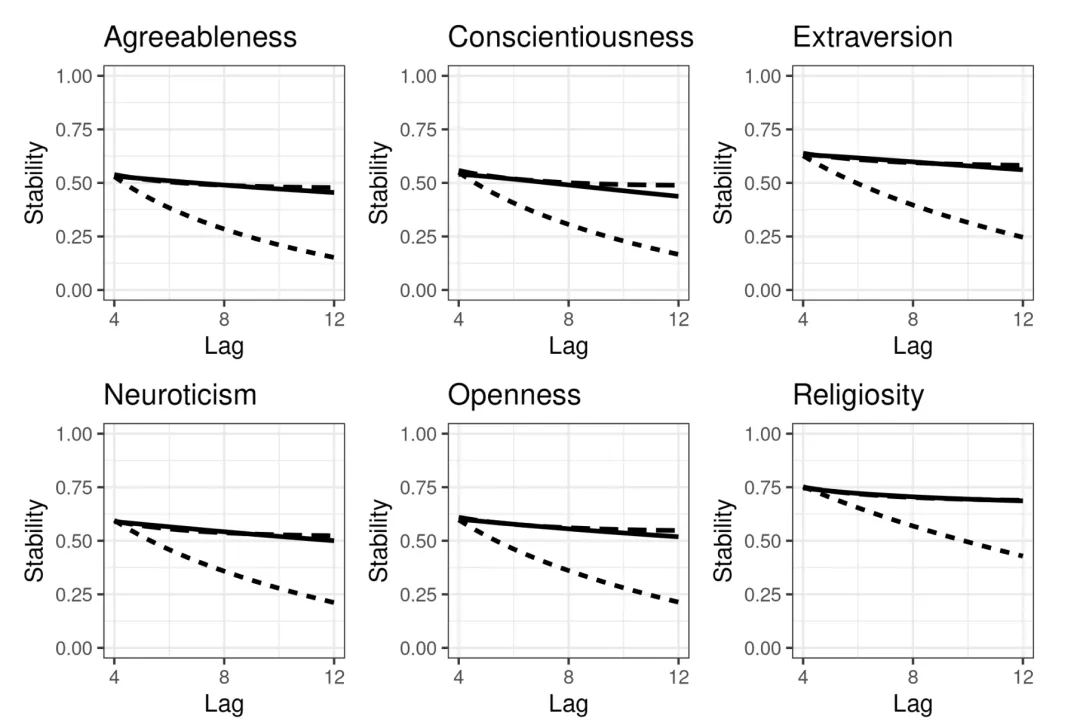
第一步：观察长期积累的相关性

首先，作者把所有波次的数据汇总在一起，检验了宗教与大五人格各维度之间的整体相关性。

Lucas对此的逻辑是：

如果人格和宗教之间真的存在长期且相互强化的因果关系，那么经过12年的不断影响，这种累积效应应该会反映在它们的相关系数上。

也就是说，我们理应观察到两者之间有较强的相关性。

但实际结果却令人意外：从数据来看，整体相关性非常微弱。

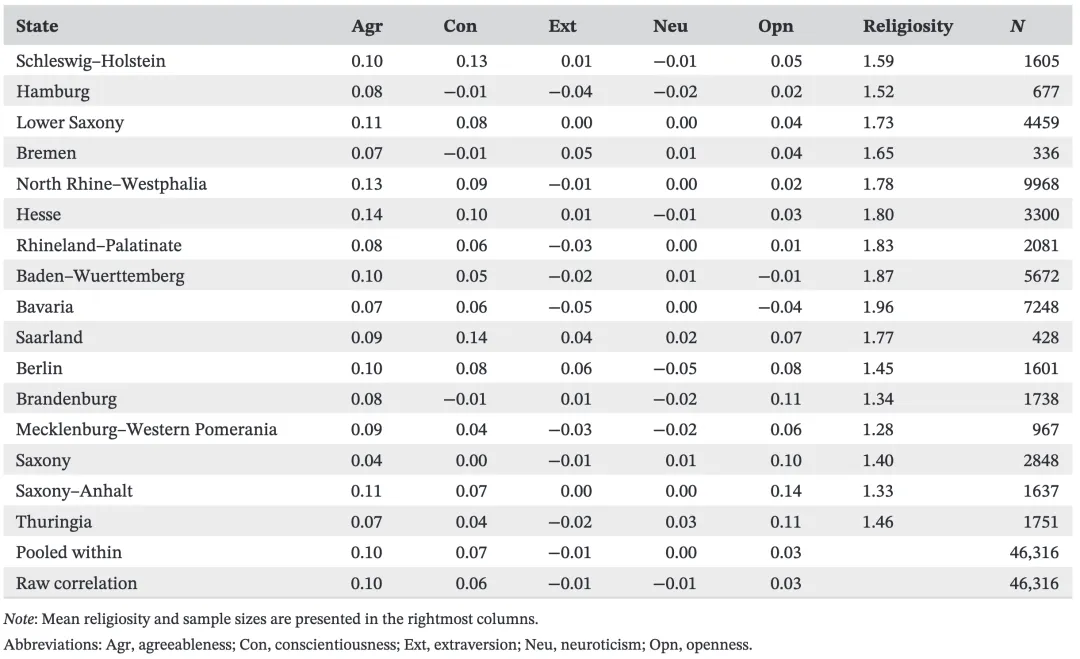
各人格特质与宗教在“个体内”及“个体间”的相关性

在不区分地区的总样本中，相关性最高的是宜人性，但也仅有0.10；

即便分地区来看，最高的相关系数也才0.14。

结论：这种微弱的相关水平，显然很难支撑起原研究中所谓的“强有力且双向的因果关系”。

第二步：多模型组合的“稳健性大检验”

为了彻底检验原研究结论的可靠性，Lucas并没有只跑一个模型，而是进行了模型之间的“排列组合”。

他按照观测变量/潜变量、全特质/单特质纳入、CLPM/RI-CLPM这三个维度，一共组合出了8个不同的模型，同时完全复刻了一遍原研究的CLPM模型，进行对比。

在此，我们先了解一下RI-CLPM。

在之前的内容讲到CLPM容易混淆“底色”和“变化”，而RI-CLPM解决了这个问题。

它通过设置随机截距，把个体间稳定的“底色”剥离出来，剩下的部分才用来分析个体内的动态变异。

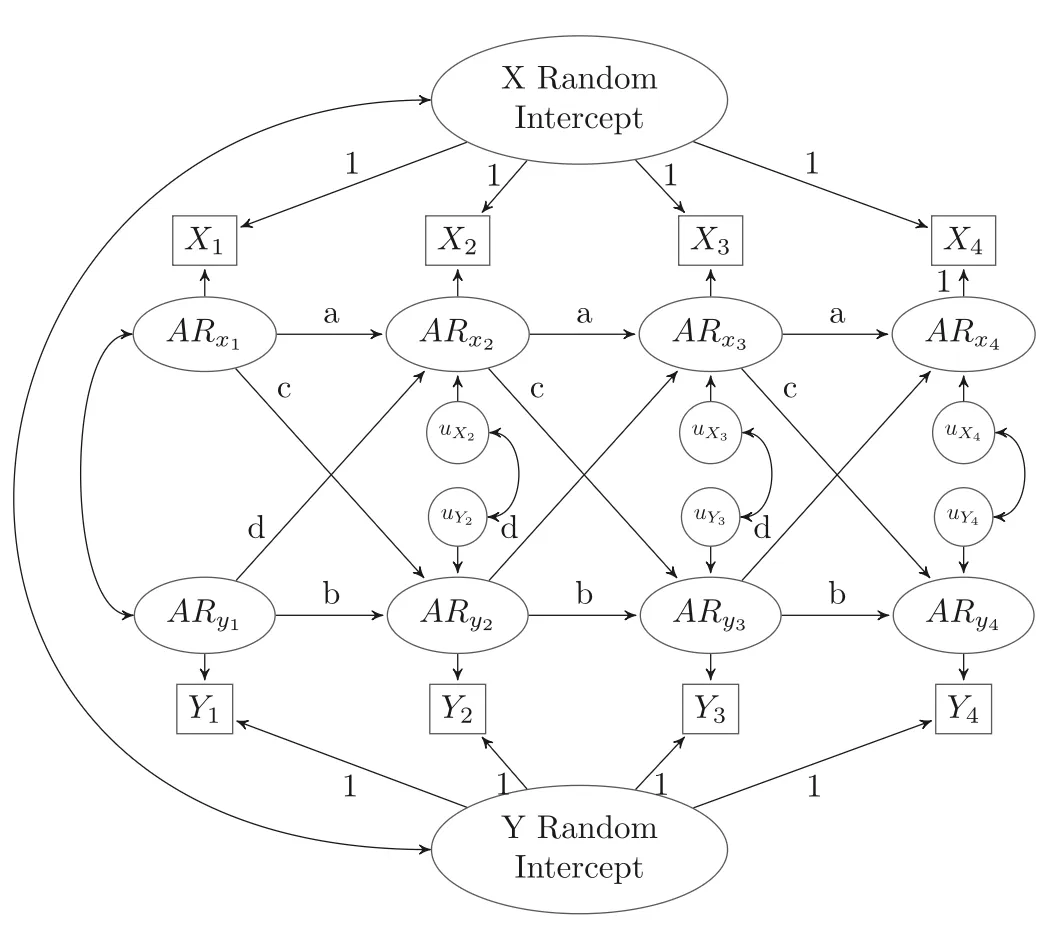
RI-CLPM路径图

再用刚才“饭量与体重”的例子：RI-CLPM会先给每个孩子划一条他自己的“饭量均线”和“体重均线”。

它不看小明是不是比小红吃得多，它只看小明自己：如果小明今年心情好，比他平时的平均饭量多吃了一碗，那么明年他的体重是否会比他平时的平均体重更重一点？

这一通分析下来，Lucas发现了三个非常硬核的结果。

拟合优度完胜：不论是潜变量还是观测变量，不论特质是同时还是单独纳入，RI-CLPM的模型拟合度都显著优于传统的CLPM。

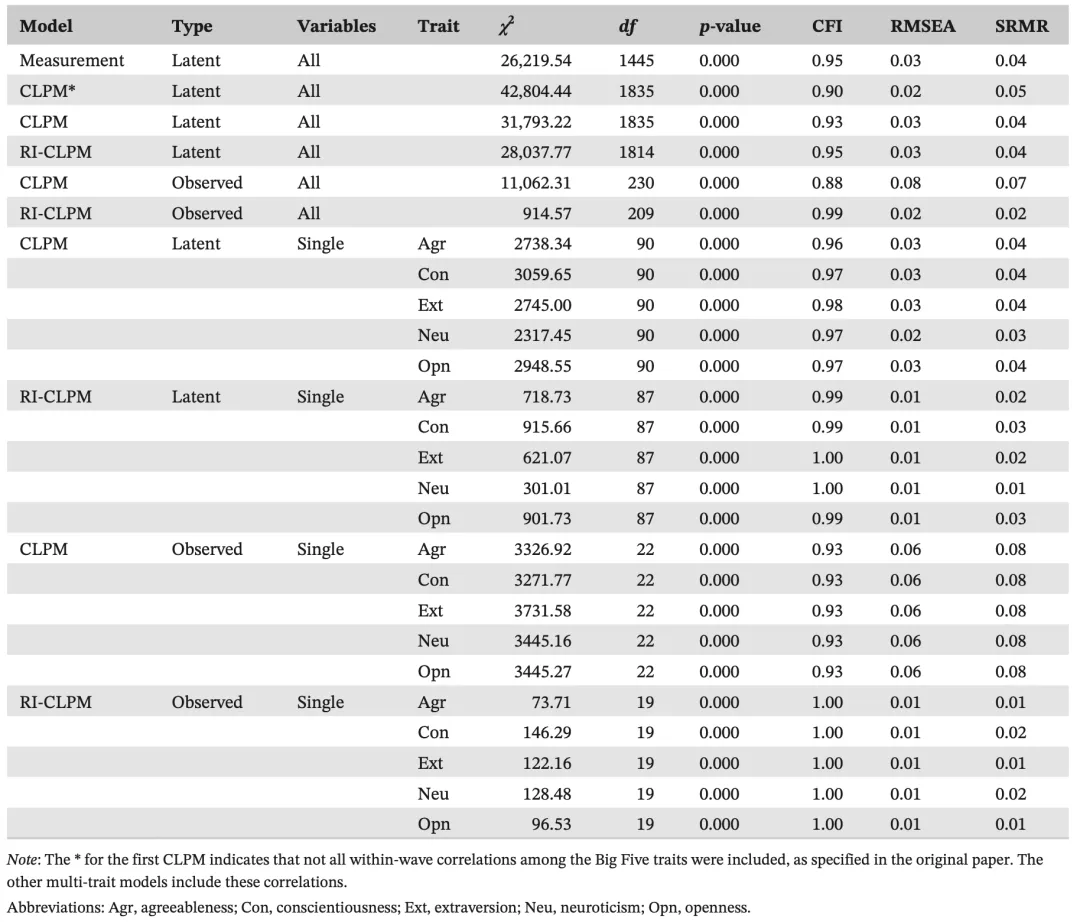
各模型拟合优度

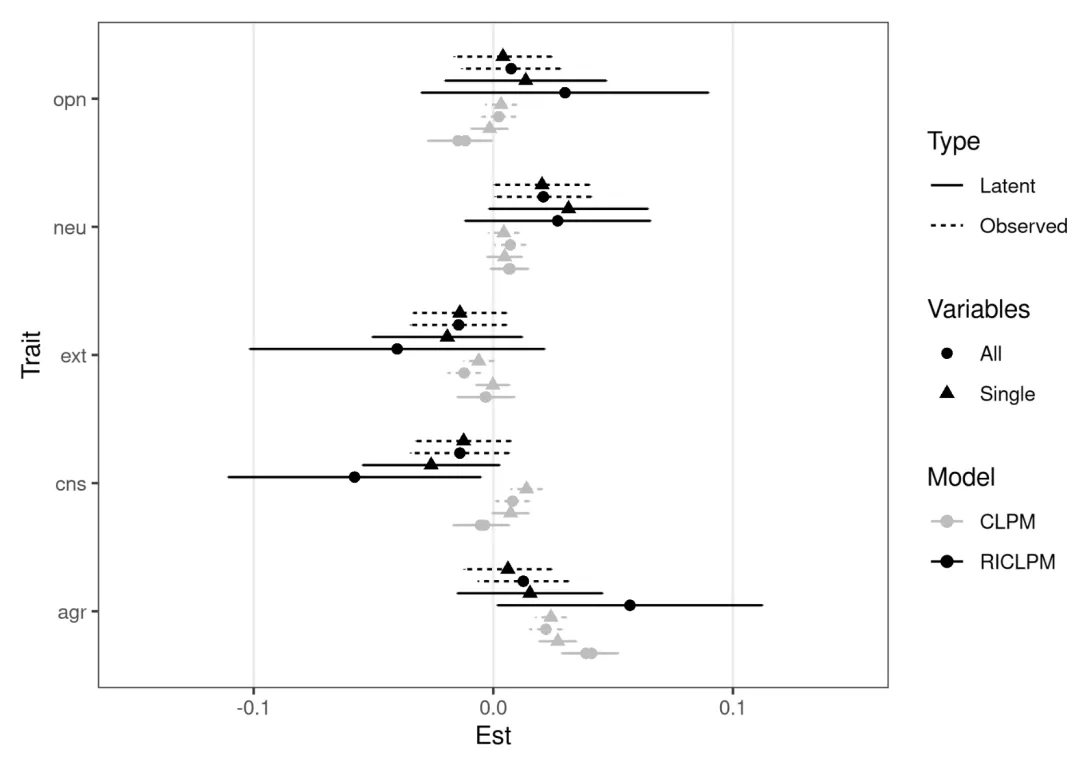
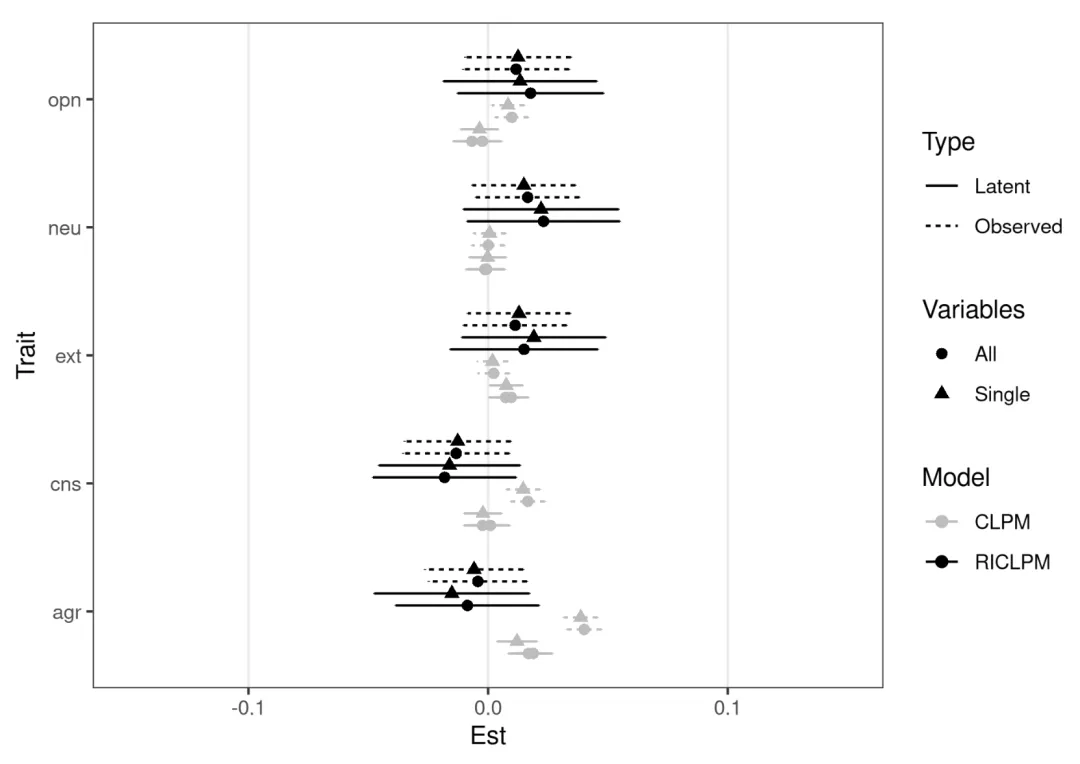
地区对“人格对宗教滞后效应”的调节效应分析

结论：这一步复核有力地支撑了Lucas的观点——原研究的结论并不稳健。

选择不同的模型，结果可能天差地别，而更符合现实规律的RI-CLPM告诉我们：人格和宗教之间的双向因果可能并不存在。

第三步：动态面板模型DPM

最后，Lucas还使用了一个更复杂的工具——动态面板模型（DPM），用它再次分析了数据，并与CLPM和RI-CLPM的结果进行了对比。

为什么要大费周章再加一个DPM呢？

这其实是为了回应学术界对RI-CLPM的一个主要质疑：RI-CLPM虽然剥离了“个体底色”的干扰，但也因为它把底色完全剥离不看了，导致它无法检验到一个人的稳定特质是否会对另一个变量的长期变化趋势产生影响。

而这恰恰是很多研究者关心的。

还是用“饭量与体重”来举例：RI-CLPM的局限在于它把小明“天生大块头”这个底色给过滤掉了。

DPM的逻辑是它既承认小明天生大块头饭量大（稳定特质），而且在分析时并不会像RI-CLPM那样为了追求“纯净”而把这个底色剥离掉。

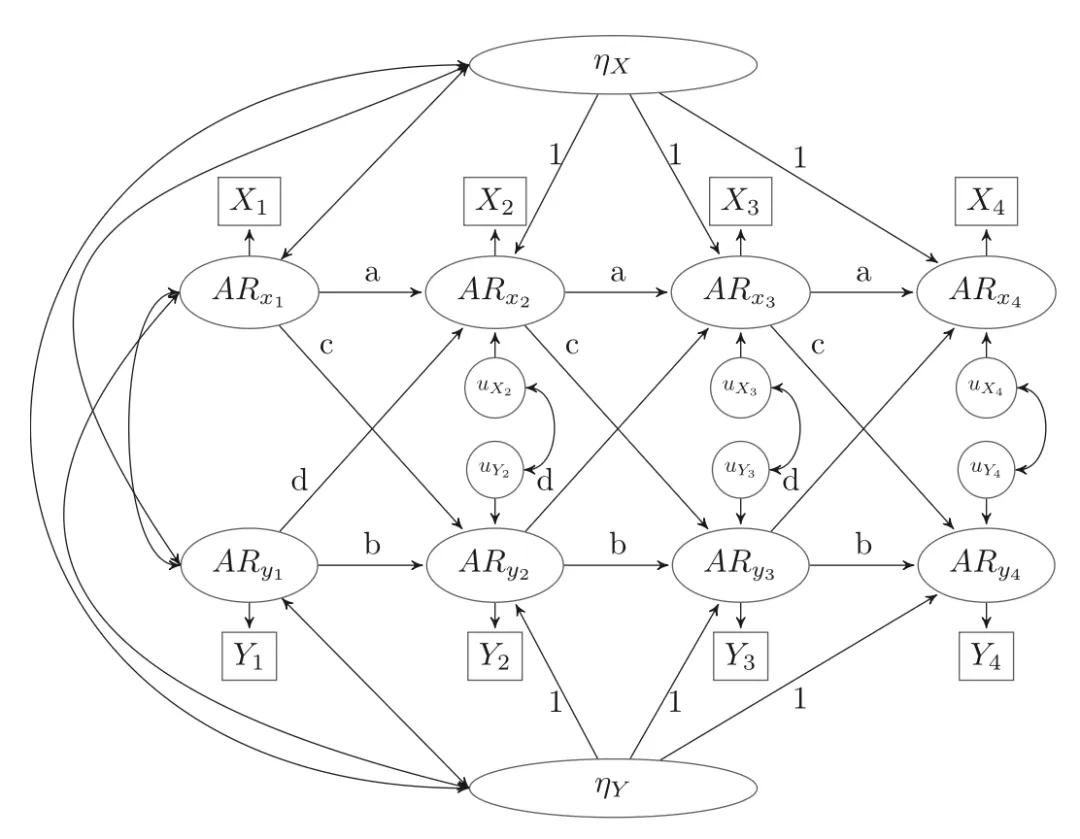
DPM路径图

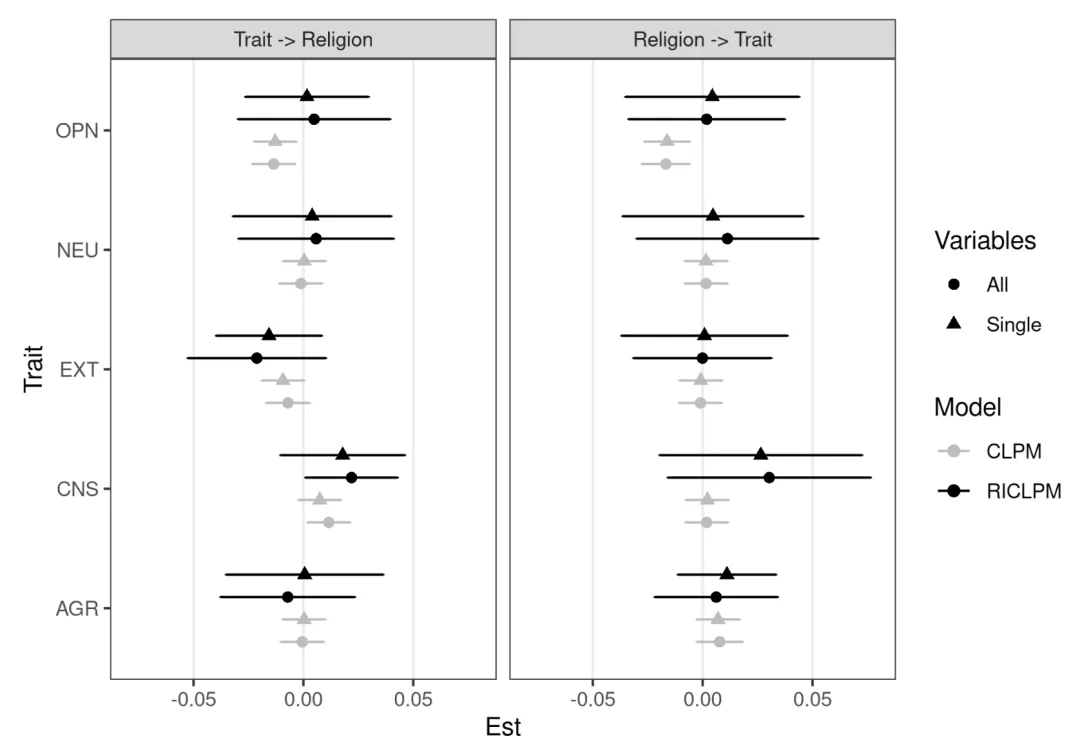
简单来说，DPM结合了CLPM和RI-CLPM的优点：它既承认个体差异的稳定性，又允许这种稳定性作为“动力源”，持续影响未来的动态变化过程。

分析结果从图中可以看到，相比于CLPM，DPM得出的结果与RI-CLPM高度相似。

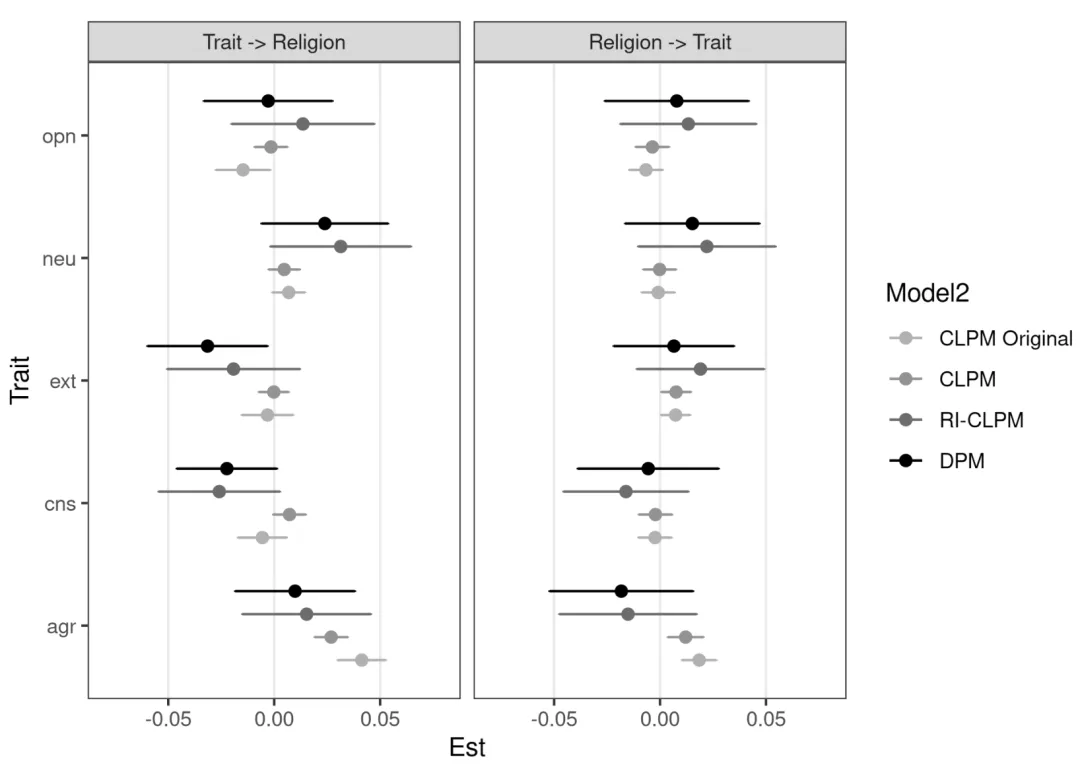
DPM、CLPM、RI-CLPM与原研究的CLPM的结果比较

这进一步佐证了Lucas的观点：由于DPM这种更严谨的模型也跑出了和RI-CLPM类似的结果，说明传统的CLPM确实存在稳健性问题。

换句话说，RI-CLPM虽然简化了底色，但在捕捉变量间关系上，比CLPM更靠谱。

对于人格与宗教这种存在双向因果、且高度稳定、难以操纵的变量，纵向追踪研究确实是最佳选择。

但基于Lucas在本文的操作，可以得到以下几点实操建议。

观测变量vs潜变量：精确性与复杂度的博弈

虽然潜变量分析能通过统计手段抵消测量误差，但它是一把双刃剑。

尤其在RI-CLPM这种本身就很复杂的模型中，引入潜变量会极大增加模型错误设定的风险，甚至导致模型无法收敛。

相比之下，使用观测变量进行分析，模型会更简洁、更稳健。

全特质纳入vs单特质分析：解释力的代价

在研究大五人格时，是把五个特质全部纳入模型，还是逐一分析？

Entringer等人的原研究选择“全纳入”，虽然控制了共线性，但代价是让分析的对象变成了“数学残差”。

在自己的研究中，我们需要警惕：当一个变量被扣除了它与其他变量共有的核心特征后，剩下的残差是否还具备原本的心理学意义？

为什么不直接用这其中最优的DPM？

既然DPM结合了CLPM和RI-CLPM的优势，为什么Lucas不直接推崇DPM？

首先，从原文的分散表述中可以得知，DPM的模型复杂度极高。

在处理像本文这样的大规模样本时，其运行的时间和算力成本（或计算开销）巨大。

其次，Lucas引入DPM的首要目的是“稳健性检验”。

他通过证明“不剥离底色（DPM）”和“剥离底色（RI-CLPM）”得出了相同的结论，从而有力地回击了针对RI-CLPM的质疑，让他对于CLPM的反驳形成了完整的逻辑闭环。

最后，一起来解读一下作者的分析代码。

这样，在自己的纵向研究中，也可以复刻这些模型来探索因果关系。