当前位置：首页>python>我的Python100天打卡:55/100 第十五章 Numpy常见运算/一维数组的加减乘除、乘幂/广播原则

我的Python100天打卡:55/100 第十五章 Numpy常见运算/一维数组的加减乘除、乘幂/广播原则

2026-01-31 05:13:06

#鸢尾花数学大系

挑战100天持续练习Python

今天是第55天

---

上次笔记，完成了第十四章Numpy数组的一维、二维、三维索引和切片的练习题，巩固了相关的切片知识。

今天来挑战第十五章！具体内容包括：

15.1 一维数组和二维数组的加减乘除、乘幂

15.2 广播原则（包括一维数组和标量、一维数组和列向量、二维数组和标量、二维数组和一维数组、二维数组和列向量）

首先先看本章思维导图：

15.1.1 一维数组的加减乘除、乘幂

1️⃣基本运算代码如下：

# 1. 加法：运算符+，或使用numpy.add()

# 2. 减法：运算符-，或使用numpy.subtract()

# 3. 乘法：运算符*，或使用numpy.multiply()

# 4. 除法：运算符/，或使用numpy.divide()

# 5. 乘幂：运算符**，或使用numpy.power()

2️⃣一维数组

首先，先让AI给我框架，我自己思考关键代码，以呈现下方一维数组的加减乘除和乘幂运算：

（1）先来引入头文件和进行数组定义（关键：np.array()）：

import numpy as npimport matplotlib.pyplot as plt# 练习1.1：创建两个相同形状的一维数组# 创建数组a，包含元素 [-2, -1, 0, 1, 2]# 【思考：如何用NumPy创建这个数组？可以用什么函数？】a = np.array([-2, -1, 0, 1, 2])# 我一开始想用“a = [-2, -1, 0, 1, 2]”，但其实这是“list”，并不符合“数组”的含义# 因此，修改为“np.array()”的表示形式# 由此，也更清晰地认识到：NumPy数组支持向量化运算（如逐元素加减乘除）和 .shape等属性，而普通列表不支持这些# 创建数组b，包含元素 [2, 2, 2, 2, 2]b = np.array([2, 2, 2, 2, 2])print("数组a:", a)print("数组b:", b)print("数组a的形状:", a.shape)print("数组b的形状:", b.shape)print()

（2）再来尝试进行数组的加减乘除、乘幂（比预想的简单和直观！）：

# 练习1.2：实现图15.1中的五种基本运算# 1. 加法add_result = a + b # 【思考：如何对两个数组进行逐元素加法？】➡️我试着直接加，结果真的一次成功！很奇妙哦！print("加法结果 (a + b):", add_result)# 2. 减法sub_result = a - b print("减法结果 (a - b):", sub_result)# 3. 乘法mul_result = a * b print("乘法结果 (a * b):", mul_result)# 4. 除法div_result = a / b print("除法结果 (a / b):", div_result)# 5. 乘幂power_result = a ** b print("乘幂结果 (a ** b):", power_result)print()

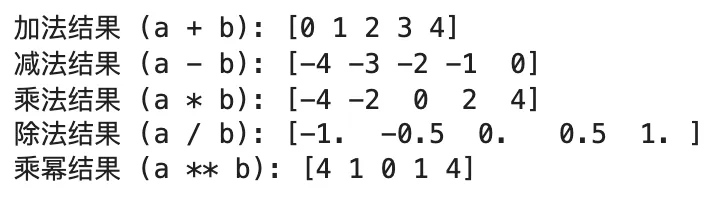
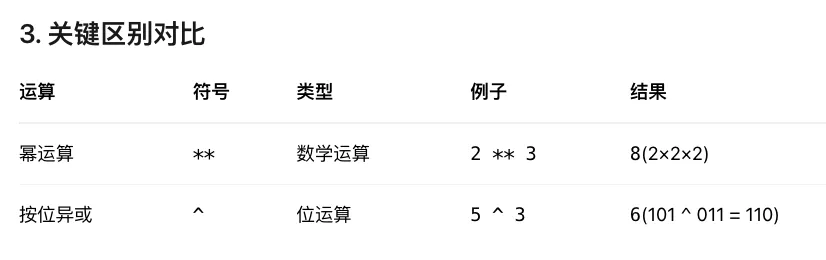
（3）需要注意的是：乘幂（**）和按位异或（^）是两种完全不同的运算方式，请参考AI给出的例子和解释：

15.1.2 二维数组的加减乘除、乘幂

1️⃣先创建二维numpy数组：

# 练习2.1：创建两个相同形状的二维数组# 创建数组A，形状为3×3# 【思考：如何用NumPy创建二维数组？有哪些方法？】# ⬇️我的思考：Numpy创建二维数组，跟一维数组类似，也是用np.array()，# 只不过里面的元素由[[a],[b],...,[n]]构成A = np.array([[-2, -1, 0],              [1, 2, 3],              [4, 5, 6]])# 创建数组B，形状为3×3B = np.array([[2, 2, 2],              [2, 2, 2],              [2, 2, 2]])print("二维数组A:")print(A)print("\n二维数组B:")print(B)print("\n数组A的形状:", A.shape)print("数组B的形状:", B.shape)print()

2️⃣计算二维numpy数组的加减乘除、乘幂（与一维数组类似）：

# 练习2.2：实现二维数组的逐元素运算# 1. 加法add_2d = A + B   # 沿用跟一维数组类似的结构print("加法结果 (A + B):")print(add_2d)print()# 2. 减法sub_2d = A - Bprint("减法结果 (A - B):")print(sub_2d)print()# 3. 乘法（非矩阵乘法）mul_2d = A * Bprint("乘法结果 (A * B):")print(mul_2d)print()# 4. 除法（自动排除除数为0的情况）div_2d = A / Bprint("除法结果 (A / B):")print(div_2d)print()# 5. 乘幂power_2d = A ** Bprint("乘幂结果 (A ** B):")print(power_2d)print()

3️⃣可视化二维numpy数组的运算结果（以A+B为例）：

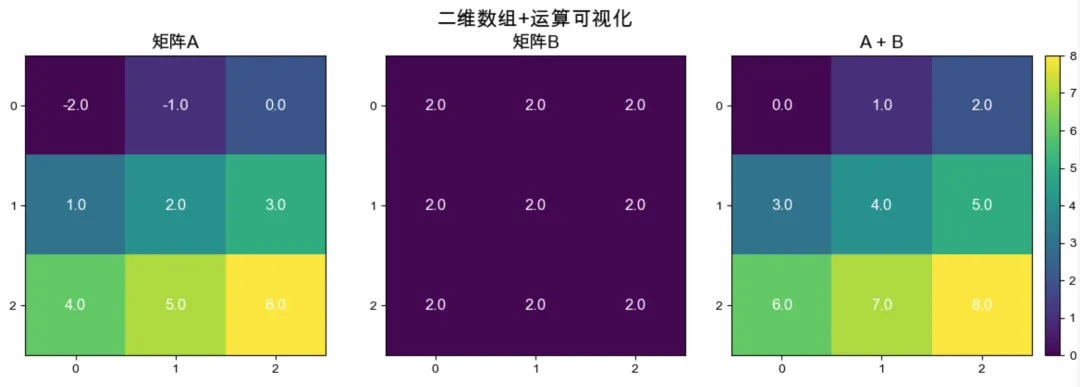
15.2 广播原则

简单来说，Numpy的广播原则（broadcasting），指定了不同形状的数组之间的算术运算规则，将形状较小的数组，扩展为形状较大的数组，使之大小相同，再进行运算，以提高效率。

15.2.1 一维数组和标量

1️⃣先创建一维数组和标量：

import numpy as npimport matplotlib.pyplot as plt# 练习2.1：一维数组和标量的运算（图15.3）# 创建一个一维数组arr_1d = np.array([-2, -1, 0, 1, 2])scalar = 2  # 标量# 我注意到，“标量”只是一个数值，但Numpy会自动将其适配广播原则，使其能够适配需要进行运算的数组的维度，我的理解正确吗？# ⬆️AI说对哦 ^w^print("一维数组:", arr_1d)print("标量:", scalar)print()

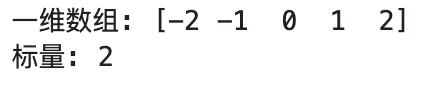
2️⃣再对一维数组和标量进行五种运算：

# 实现标量与数组的五种运算# 【思考：标量如何与数组的每个元素进行运算？】scalar_add = arr_1d + scalar # 【提示：直接用 + 运算符】scalar_sub = arr_1d - scalar # 【提示：直接用 - 运算符】scalar_mul = arr_1d * scalar # 【提示：直接用 * 运算符】scalar_div = arr_1d / scalar # 【提示：直接用 / 运算符】scalar_power = arr_1d ** scalar # 【提示：直接用 ** 运算符】print("一维数组 + 标量:", scalar_add)print("一维数组 - 标量:", scalar_sub)print("一维数组 × 标量:", scalar_mul)print("一维数组 ÷ 标量:", scalar_div)print("一维数组 ^ 标量:", scalar_power)print()

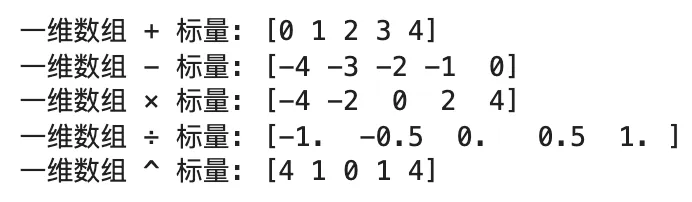
3️⃣心得：上面的“标量”还是比较容易理解的；但下面几个学习，就比较抽象了，一个个来看吧：

15.2.2 一维数组和列向量

首先，还是先用一个可视化图片，来解释下“一维数组”和“列向量”相加后的变化：

（1）这是原来的“一维数组”和“列向量”，请注意各自的形状：

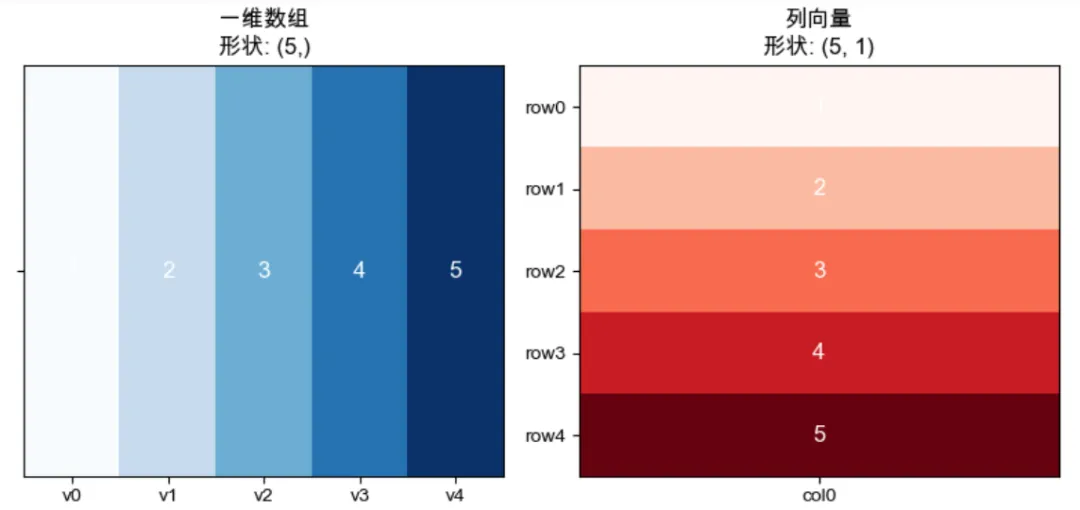
（2）这是它们相加后的结果，请注意其形状：

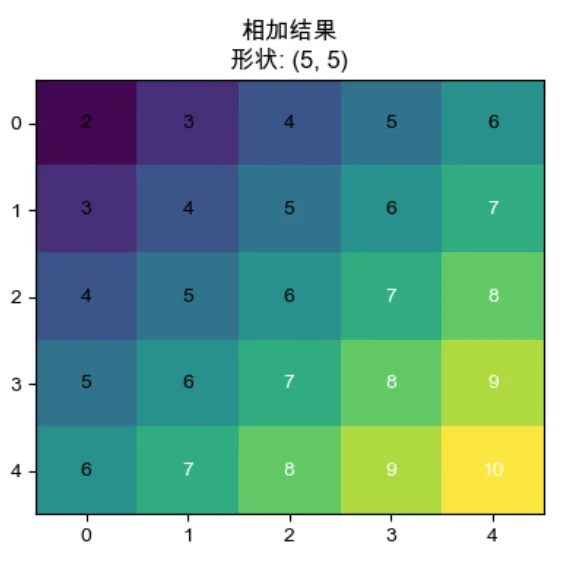
（3）用文字逐步解释上述过程：

15.2.4 二维数组和一维数组

有了之前的铺垫，现在来看看“二维数组”和“一维数组”的相加：

1️⃣首先看书本给到的例子：

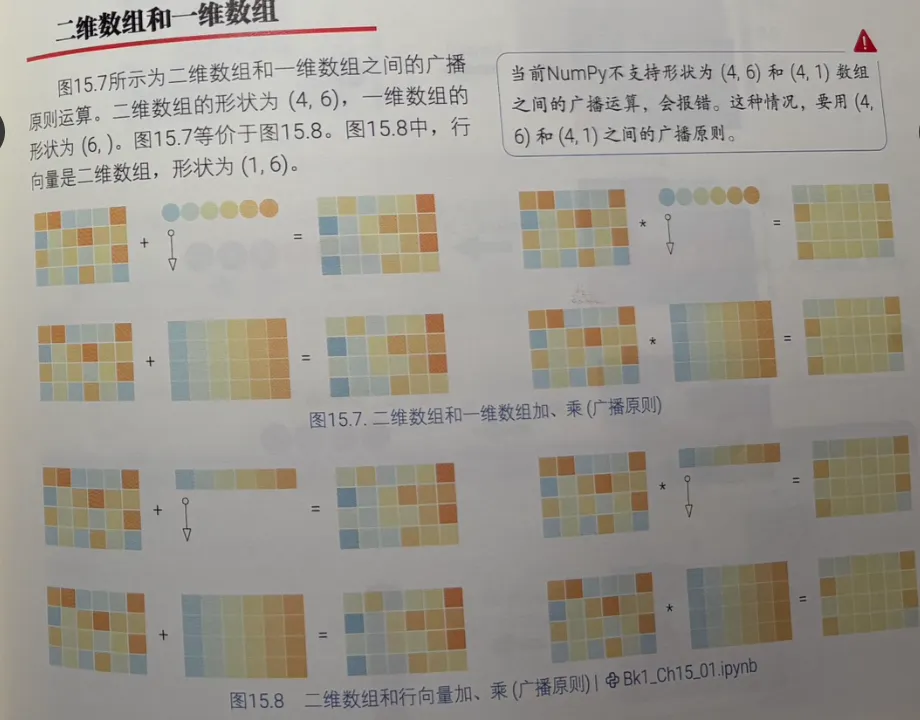
2️⃣再填写AI给的框架，用注释记录自己的思考：

# 练习2.5：二维数组和一维数组的运算（图15.7）# 创建二维数组 (4,6)arr_2d = np.array([[1, 2, 3, 4, 5, 6],                   [7, 8, 9, 10, 11, 12],                   [13, 14, 15, 16, 17, 18],                   [19, 20, 21, 22, 23, 24]])# 创建一维数组 (6,)arr_1d_6 = np.array([1, 2, 3, 4, 5, 6])print("二维数组 (形状 {}):".format(arr_2d.shape))print(arr_2d)print("\n一维数组 (形状 {}):".format(arr_1d_6.shape))print(arr_1d_6)print()# 实现二维数组和一维数组的加法# 【思考：形状(4,6)和(6,)如何相加？广播原则如何应用？】broadcast_2d_1d = arr_1d_6 + arr_2d # 【提示：直接相加，注意广播方向】print("二维数组 + 一维数组 (广播加法):")print("结果形状:", broadcast_2d_1d.shape)print("结果:\n", broadcast_2d_1d)print()

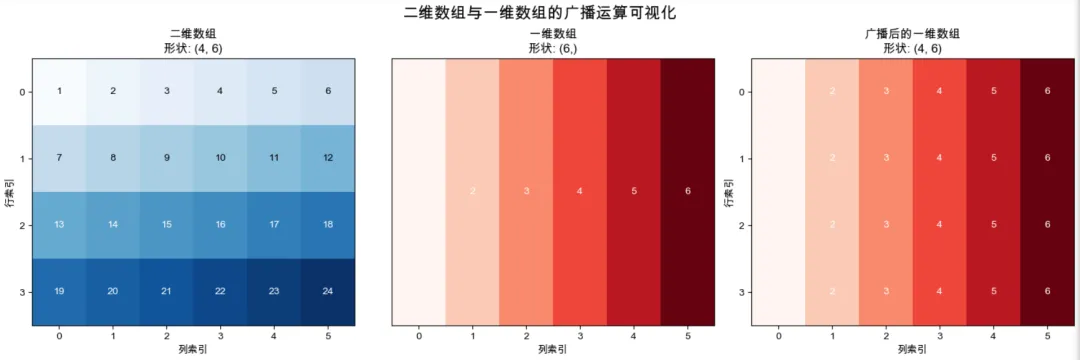
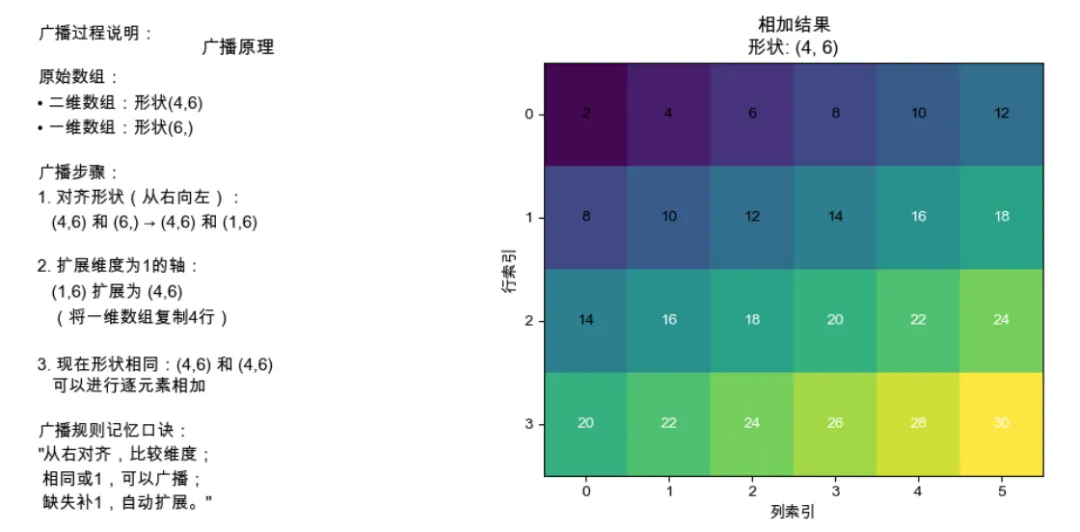
15.2.5 二维数组和列向量

1️⃣书本主要探讨了二维数组和列向量在加法和乘法方面的广播原则。

2️⃣AI教练则给了更广泛的数组形状，用“循环➕一个个测试”的方法，将不同形状的数组进行配对，突出一个“举一反三”的作用！详见下方代码：

# 练习2.7：广播原则的边界情况# 测试一些广播规则test_cases = [    (np.array([1, 2, 3]), np.array([[1], [2], [3]])),  # (3,) 和 (3,1)    (np.array([[1, 2, 3]]), np.array([[1], [2], [3]])),  # (1,3) 和 (3,1)    (np.array([1, 2, 3]), np.array([1, 2])),  # 不兼容的形状]print("广播规则测试:")for i, (arr1, arr2) in enumerate(test_cases, 1):    print(f"\n测试案例 {i}:")    print(f"数组1 形状: {arr1.shape}")    print(f"数组2 形状: {arr2.shape}")    try:        # 【提示：尝试相加】        result = arr1 + arr2        # ⬆️问了AI，才知道可以用如此简洁的方式，尝试将不同形状的数组相加～        print("可以广播，结果形状:", result.shape)    except ValueError as e:        print(f"不能广播: {e}")