动手时刻:Python 仿真 QKD 网络 (上) —— 搭建不完美的物理层

昨天，我们在云端俯瞰了宏大的 Q-SDN 网络架构。今天，我们要降落到地面，打开代码编辑器，开始干脏活累活了。

物理学家费曼曾说过：“What I cannot create, I do not understand.（我不能创造的，我就没真正理解。）”

你可能觉得你懂 BB84 协议了：不就是随机选基、比对、丢弃吗？ 但当你真正试图用代码去模拟它时，你会遇到无数现实的问题：

• 光子在信道里飞的时候，怎么模拟“噪声”？
• Bob 选错基的时候，代码逻辑怎么写才能体现“50% 随机性”？
• 最后的误码率（QBER）到底是怎么算出来的？

今天，我们将编写一套 QKD 仿真器。 我们将不再写几行简单的脚本，而是采用 面向对象 (OOP) 的正规工程思维，构建 Alice、Bob 和 Quantum Channel 三个核心类。

我们的目标是：模拟发送 10,000 个光子，经过有噪声的信道，完成筛选（Sifting），并统计出最终的误码率。

打开你的 IDE（VS Code / PyCharm / Jupyter），把昨天的环境准备好。Let's Code!

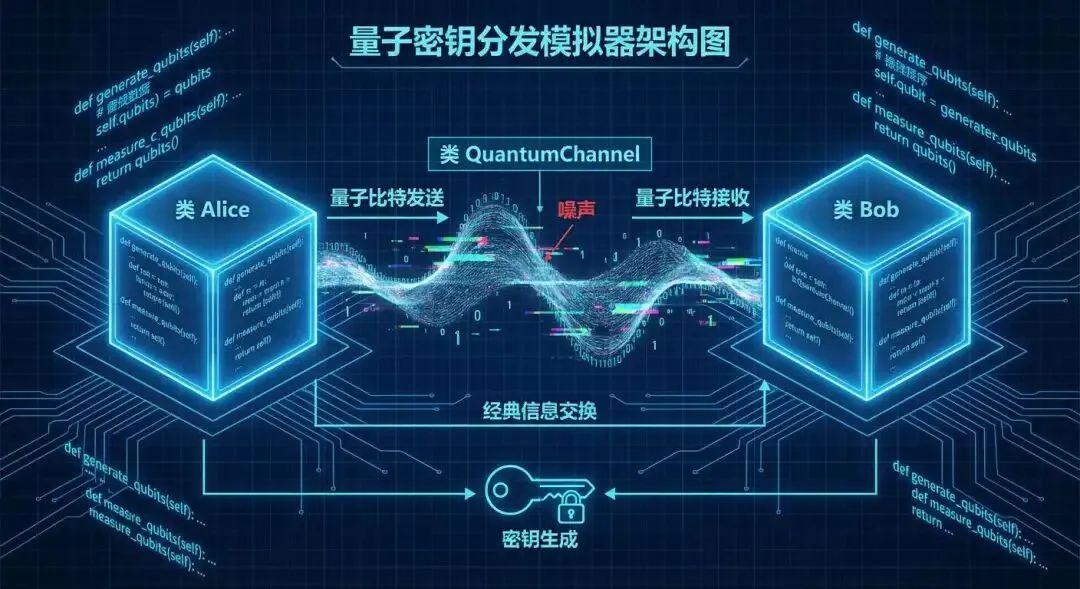
上帝视角 —— 系统架构设计

在敲下第一行代码之前，优秀的工程师都会先画图。 我们要构建的仿真器包含三个核心对象：

1. QuantumChannel (量子信道)：

• 这是环境。它是“上帝”的地盘。
• 它负责传输光子。
• 关键特性：它是不完美的。我们要在里面加入noise_rate（噪声率），模拟光子在传输过程中发生比特翻转（Bit Flip）的情况。

2. QNode (量子节点)：

• 这是一个父类。Alice 和 Bob 都是节点，他们有共性。
• 共性：都需要选择基矢（Basis），都需要处理比特（Bit）。

3. SimulationManager (仿真管理器)：

• 这是“主程序”。
• 负责协调流程：Alice 发 -> Channel 传 -> Bob 收 -> 双方对基 -> 统计结果。

构建物理层 —— 充满噪声的信道

首先，我们来写最核心的“环境”——信道。 在真实的物理世界中，噪声来源很多（热噪声、暗计数、光纤双折射）。 在我们的仿真模型中，我们将其简化为 BSC 模型 (Binary Symmetric Channel，二进制对称信道)： 即：光子有  的概率发生比特翻转（0变1，1变0），或者发生相位翻转（我们暂只模拟比特翻转）。

新建文件 qkd_sim_v1.py，写入以下代码：

import numpy as np

# ==========================================
# 0. 基础配置
# ==========================================
# 为了方便理解，我们定义常数
BASIS_Z = 0# 标准基 (+)：对应 0°/90°
BASIS_X = 1# 对角基 (x)：对应 45°/135°

classQuantumChannel:
"""
    模拟量子信道。
    职责：传输量子态，并引入噪声。
    """
def__init__(self, noise_rate=0.0):
        self.noise_rate = noise_rate
        print(f"[System] 信道初始化完毕。物理噪声率设定为: {noise_rate * 100}%")

deftransmit(self, photon_stream):
"""
        传输光子流。
        :param photon_stream: Alice 发出的光子列表 [{'bit':0, 'basis':1}, ...]
        :return: 到达 Bob 端的光子列表 (可能已发生翻转)
        """
        output_stream = []
        error_count = 0

for p in photon_stream:
# 复制一份光子数据，避免修改原数据（模拟光子离开 Alice）
            current_photon = p.copy()

# === 模拟噪声干扰 ===
# 生成一个 0~1 的随机数，如果小于噪声率，则发生翻转
if np.random.rand() < self.noise_rate:
# 比特翻转：0->1, 1->0
                current_photon['bit'] = 1 - current_photon['bit']
                error_count += 1

            output_stream.append(current_photon)

        print(f"[Channel] 传输完成。传输 {len(photon_stream)} 个光子，"
f"因噪声翻转了 {error_count} 个比特。")
return output_stream

代码解析： 这段代码虽然简单，但它模拟了通信中最本质的属性：不确定性。np.random.rand() < self.noise_rate 这行代码，就是上帝掷出的那个骰子。在后续的过程中，Eve 的攻击也会在这里发生。

主角登场 —— Alice 与 Bob 的类设计

接下来，我们要定义 Alice（发送者）和 Bob（接收者）。 为了代码复用，我们先写一个父类 QNode。

classQNode:
"""量子节点的基类"""
def__init__(self, name):
        self.name = name
        self.bits = []   # 存储比特
        self.bases = []  # 存储基矢

defclear_memory(self):
        self.bits = []
        self.bases = []

Alice：制备与发送

Alice 的任务是：生成随机比特，选择随机基矢，然后把它们打包成光子发出去。

classAlice(QNode):
defprepare_photons(self, n_photons):
"""
        制备 N 个光子
        """
        print(f"[{self.name}] 正在制备 {n_photons} 个光子...")
# 1. 生成随机比特 (0 或 1)
        self.bits = np.random.randint(0, 2, n_photons)
# 2. 生成随机基矢 (0 或 1)
        self.bases = np.random.randint(0, 2, n_photons)

# 3. 打包成光子流
        stream = []
for i in range(n_photons):
            stream.append({
'bit': self.bits[i],
'basis': self.bases[i]
            })
return stream

Bob：测量与坍缩

Bob 的逻辑最复杂，因为涉及到量子力学的测量原理。

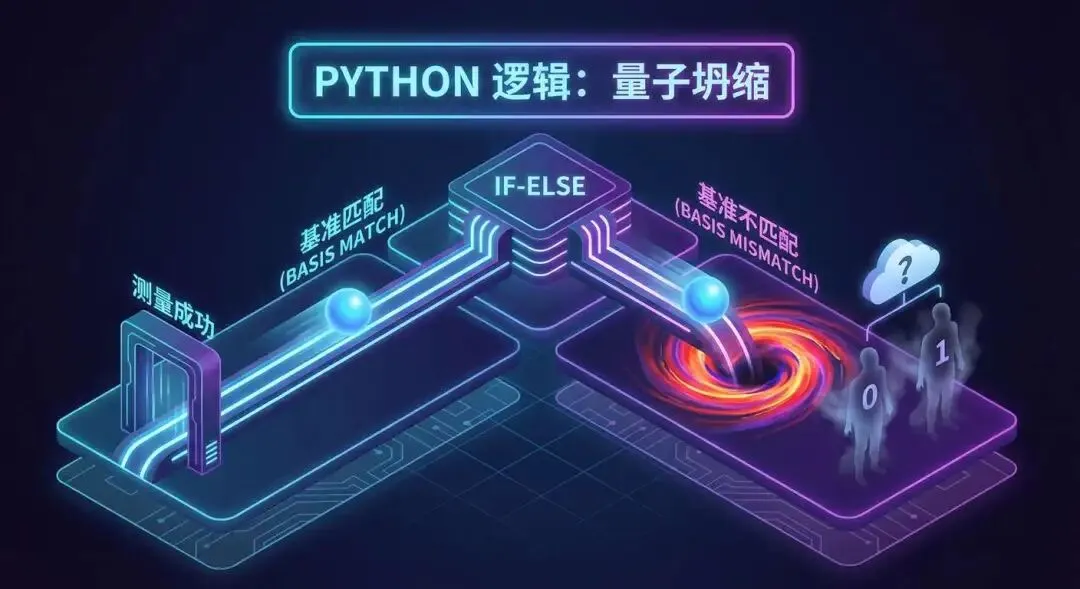
物理规则回顾：

1. 基矢相同：测量结果 = 传入的光子状态（如果不考虑噪声）。
2. 基矢不同：测量结果 = 完全随机（50% 是 0，50% 是 1）。

classBob(QNode):
defmeasure_photons(self, incoming_stream):
"""
        测量接收到的光子流
        """
        n = len(incoming_stream)
        print(f"[{self.name}] 正在测量 {n} 个光子...")

# 1. Bob 随机选择测量基矢
        self.bases = np.random.randint(0, 2, n)
        self.bits = [] # 用来存测量结果

for i in range(n):
            photon = incoming_stream[i]
            alice_basis = photon['basis']
            alice_bit = photon['bit']
            bob_basis = self.bases[i]

            measured_bit = None

# === 量子测量逻辑 ===
if bob_basis == alice_basis:
# Case A: 基矢匹配 -> 确定性结果
# (注意：这里的 alice_bit 已经是经过信道噪声后的结果了)
                measured_bit = alice_bit
else:
# Case B: 基矢不匹配 -> 坍缩到随机结果
                measured_bit = np.random.randint(0, 2)

            self.bits.append(measured_bit)

        print(f"[{self.name}] 测量完成。")

后处理 —— 筛选 (Sifting)

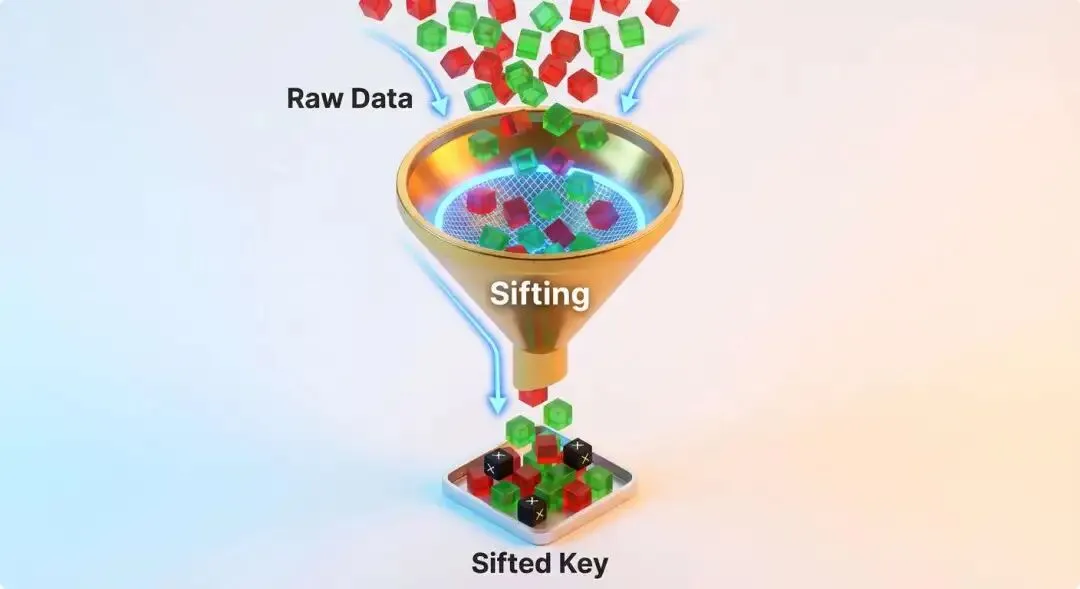
现在，光子已经跑完了全程。 Alice 手里有一串比特，Bob 手里也有一串。 但是，由于有一半的基矢是不匹配的，这两串比特现在看起来完全不一样。

我们需要进行 Sifting（基矢比对），把那些“牛头不对马嘴”的数据剔除掉。

在主程序中添加筛选逻辑：

defrun_sifting(alice, bob):
"""
    模拟经典信道上的基矢比对过程
    """
    print("\n=== 开始后处理: 筛选 (Sifting) ===")

    sifted_alice_bits = []
    sifted_bob_bits = []
    match_indices = []

    total_count = len(alice.bases)

for i in range(total_count):
# Alice 和 Bob 公开通过经典信道对比基矢
if alice.bases[i] == bob.bases[i]:
            match_indices.append(i)
            sifted_alice_bits.append(alice.bits[i])
            sifted_bob_bits.append(bob.bits[i])

    print(f"原始长度: {total_count}")
    print(f"筛选后长度: {len(sifted_alice_bits)} (约为原始的一半)")

return sifted_alice_bits, sifted_bob_bits

跑起来！—— 完整的仿真实验

最后，我们将所有模块组装起来，进行一次完整的实验。 我们将设置噪声率为 5%，看看最终的误码率是多少。

if __name__ == "__main__":
# 1. 初始化环境
    N_PHOTONS = 10000
    NOISE_LEVEL = 0.05# 5% 的信道噪声

    channel = QuantumChannel(noise_rate=NOISE_LEVEL)
    alice = Alice("Alice")
    bob = Bob("Bob")

# 2. 量子传输阶段
    print("\n--- Phase 1: 量子传输 ---")
# Alice 制备
    photons = alice.prepare_photons(N_PHOTONS)
# 信道传输 (引入噪声)
    noisy_photons = channel.transmit(photons)
# Bob 测量
    bob.measure_photons(noisy_photons)

# 3. 后处理阶段
    print("\n--- Phase 2: 后处理 ---")
# 筛选
    final_key_a, final_key_b = run_sifting(alice, bob)

# 4. 结果分析：计算误码率 (QBER)
# 注意：在真实 QKD 中，我们只能抽取一小部分来算 QBER
# 但在上帝模式仿真中，我们可以对比全部密钥来验证理论

    errors = 0
    final_len = len(final_key_a)
for i in range(final_len):
if final_key_a[i] != final_key_b[i]:
            errors += 1

    qber = errors / final_len if final_len > 0else0

    print("\n=== 最终实验报告 ===")
    print(f"设定噪声率 : {NOISE_LEVEL * 100:.2f}%")
    print(f"最终 QBER  : {qber * 100:.2f}%")

if qber < 0.11:
        print(">> 状态: 安全。可以进行下一步纠错。")
else:
        print(">> 状态: 危险！误码率过高，可能存在窃听或信道故障。")

深入分析 —— 为什么 QBER 和噪声率一样？

运行上述代码，你会发现一个有趣的现象： 如果你的 NOISE_LEVEL 设为 0.05 (5%)，那么最终算出来的 QBER 大约也是 5%。

读者提问：“这不废话吗？噪声是 5%，错误率当然是 5%。”

且慢！ 这里有一个极其重要的物理逻辑需要你理解。 我们回顾一下 Bob 的测量过程：

1. 基矢不匹配时：Bob 瞎猜。结果 50% 对，50% 错。这一部分数据，错误率高达 50%。但是，这部分数据在 Sifting 阶段被删掉了。
2. 基矢匹配时：
• 如果信道无噪声：Alice 是 0，Bob 必测得 0。错误率 0%。
• 如果信道有噪声：Alice 是 0，信道翻转成 1，Bob 测得 1。错误率 = 翻转概率。

结论： Sifting 过程不仅仅是筛选基矢，它实际上过滤掉了因为“测量原理（测不准）”带来的那 50% 随机错误，只留下了“信道本身”带来的错误。 这就是为什么我们在后处理之后看到的 QBER，能够直接反映信道的物理质量（或 Eve 的攻击强度）。

如果 Eve 出现（比如 Day 16 的中间人攻击），她会导致基矢匹配的那部分数据也出现错误，从而拉高 QBER。我们将在下一章模拟这个过程。

结语

今天，你亲手赋予了 Alice 和 Bob 生命。 看着终端里打印出的 QBER: 5.02%，你是否感到一种掌控感？ 这不再是教科书上冷冰冰的 ，而是你自己模拟出来的真实数据。

但是，现在的 Alice 和 Bob 还是“幼稚”的。

1. 他们没有防御力：如果我把 NOISE_LEVEL 调到 20%，他们只会傻傻地报警，不会尝试修补。
2. 他们没有敌人：目前的噪声只是大自然的随机干扰，还没有那个狡猾的 Eve。

明日预告：动手时刻 (下) —— 召唤 Eve 与纠错算法实战明天，我们将升级这个仿真器。

1. 我们要写一个 class Eve，让她在信道中间进行“截获-重发”攻击。
2. 我们将亲眼看到 Eve 的出现是如何让 QBER 飙升到 25% 的。
3. 如果不幸发生了错误（QBER < 11%），我们将手写一个简化版的 Cascade 纠错算法，看看如何把那些错误的比特救回来。

代码难度会升级，请保持你的 IDE 处于热身状态。 明天见，代码构建者！

📝

1. 修改代码：尝试修改 NOISE_LEVEL 为 0.0，运行代码。你的 QBER 是多少？如果是 0.5 (50%)，说明代码逻辑有问题（Sifting 没起作用）；应该是 0.0。
2. 脑洞挑战：在目前的 Bob.measure_photons 函数中，我们假设 Bob 的探测器是完美的。试着给 Bob 也加一个参数 detector_efficiency = 0.8（探测效率 80%）。这意味着有 20% 的光子 Bob 会“漏测”（变成 None）。这会如何影响 Sifting 的逻辑？（提示：Bob 需要告诉 Alice 哪些位他没收到）。

(动手写代码，是理解量子通信最快的捷径。)