【#数学哲学 #科学基础 #宇宙法则 #东方哲学 #认知科学 #人工智能 #科学传播】

一、引言：一个震撼的思想命题

“数学，既不是科学，也不是哲学，他是科学和哲学之母，是先天科学，是先天哲学，是道的规则之因果逻辑。”

这句话初读可能令人困惑甚至怀疑，但它指向了数学哲学中最深刻、最根本的问题。在我们习以为常的认知中，数学是科学的“语言”，是哲学的“工具”，但很少有人追问：数学本身是什么？

今天，我们将打破这一常规思维，从多个维度深入探讨这一命题。你会发现，数学的定位远比我们想象的更为根本——它可能是宇宙的“先天代码”，是理性与存在之间的“终极契约”，是我们理解一切实在的“元框架”。

二、数学的“先天性”：超越经验的知识体系

2.1 康德的洞见：先天综合判断

18世纪德国哲学家康德提出了一个划时代的观点：数学是一种“先天综合判断”。所谓“先天”，指独立于一切经验；所谓“综合”，指能够扩展我们的知识。

这一观点打破了传统经验主义与理性主义的对立。数学既不像纯粹逻辑那样只是分析已有概念（如“所有单身汉都是未婚的”），也不像自然科学那样完全依赖感官经验。数学命题（如“三角形内角和等于180度”）具有必然性和普遍性，但又确实告诉了我们关于世界的实质性信息。

搜索关键词：康德 先天综合判断 数学哲学 先验知识

2.2 数学与经验科学的根本区别

伽利略曾言：“自然之书是用数学语言写成的。”这成为现代科学的信条。但我们必须清楚区分：

• 经验科学（如物理、化学、生物学）：通过观察、实验、验证/证伪来建立理论。其真理标准是与经验世界相符，且理论总是可修正、可改进的近似。

• 数学：通过定义、公理、逻辑演绎来建立定理系统。其真理标准是逻辑自洽性和内部一致性。一旦证明，便成永恒。

当我们说“1+1=2”时，我们不是在总结数苹果的经验，而是在陈述一个基于皮亚诺公理系统的逻辑必然。你可以怀疑感官（苹果会不会突然消失？），但你不能怀疑逻辑推理本身。

搜索关键词：经验科学 vs 形式科学 数学真理性 逻辑自洽性

2.3 认知科学的挑战：数学是“天生”的吗？

现代认知科学提出了有趣的反驳：人类的数学能力可能部分源于进化过程中对物理世界的适应。我们识别数量、感知空间关系的能力，确实与大脑的特定神经模块相关。

但这并不否定数学的“先天性”，只是区分了两种“先天”：

• 心理学意义上的先天：与生俱来的认知倾向或模块

• 认识论意义上的先天：独立于经验的有效性基础

数学的先天性主要指后者。即使我们的数学直觉源于进化，数学真理的逻辑有效性仍超越任何具体的认知过程。

三、数学：科学之母

3.1 科学革命的核心：数学化的世界观

科学革命的本质，不是简单的“观察更多”，而是将自然现象数学化。开普勒用椭圆方程描述行星轨道，牛顿用微积分统一天地运动，麦克斯韦用偏微分方程预言电磁波。

没有数学，现代科学理论将只是模糊的隐喻和定性描述。数学为科学“赋形”——将模糊的自然规律转化为精确、可计算、可预测的形式模型。

3.2 数学的预言力量

数学最令人震撼的特征之一，是其不可思议的预言能力。数学结构往往先于物理应用被发现，等待数十年甚至数百年后才被“认领”：

• 非欧几何（19世纪初发现） → 广义相对论（1915年）

• 群论（19世纪中叶发展） → 粒子物理标准模型（20世纪中后期）

• 矩阵力学（纯粹数学理论） → 量子力学（成为量子力学的核心数学框架）

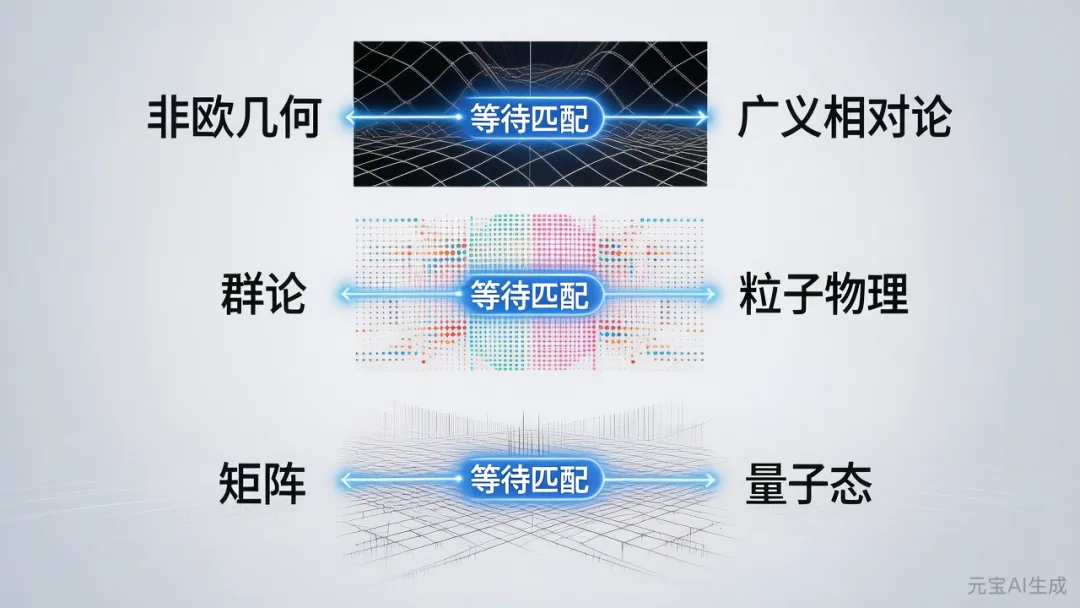
这些案例强烈暗示：数学不是人类为描述世界而发明的便利工具，而是一个独立存在的“领域”，科学家只是在“发现”早已在那里的结构。

3.3 数学宇宙假说：最激进的科学哲学观点

麻省理工学院物理学家马克斯·泰格马克提出了“数学宇宙假说”：我们的物理现实就是一个数学结构。宇宙并非“服从”数学规律，宇宙就是数学规律的具象化。

这一假说虽然激进，但能解释数学的“不合理有效性”：数学之所以能完美描述物理世界，因为物理世界本就是数学的。我们生活在“一个巨大、自洽的数学对象”中。

搜索关键词：数学宇宙假说 Max Tegmark 万物理论 宇宙是数学结构

四、数学：哲学之母

4.1 理性思维的终极典范

如果说科学展示了数学的描述力量，那么哲学则见证了数学的规范力量。数学为人类理性思维设定了最高标准：

• 何为证明？ 数学证明要求绝对严谨，每一步都必须基于明确的前提和有效的推理规则。

• 何为真理？ 数学真理一旦确立，便具有必然性、永恒性和普遍性。

• 何为清晰？ 数学概念要求精确定义，避免哲学中常见的模糊和歧义。

哲学中的分析传统，很大程度上是向数学看齐的结果——用逻辑的清晰性来解决传统哲学问题的模糊性。

4.2 数学哲学：哲学自我反思的镜子

数学本身也成为哲学最重要的反思对象之一。围绕数学本质的争论，映射了人类对知识、真理和实在的根本理解：

• 逻辑主义（罗素、怀特海）：试图将数学还原为逻辑。认为数学真理是逻辑真理的延伸。

• 形式主义（希尔伯特）：将数学视为符号操作的游戏。关注数学系统的形式一致性和完备性。

• 直觉主义（布劳威尔）：强调数学是人类心灵的构造。数学对象只存在于心智活动中。

• 柏拉图主义（哥德尔、彭罗斯）：认为数学对象客观存在，独立于物质世界和人类心智。

这些争论至今未有定论，但正是这些争论本身，推动着哲学对理性、知识和实在的深入理解。

4.3 数学与伦理：一个被忽视的连接

表面上，数学与伦理毫无关系。但深入思考，数学精神——追求真理、尊重逻辑、崇尚清晰、承认错误——本身就是一种重要的理智德性。

在一个后真相时代，数学所体现的理性精神，或许比我们想象的更为珍贵。它教会我们：有些东西比我们的偏好、情感和立场更重要——那就是逻辑和证据。

五、东方智慧：“道”的数学维度

5.1 “道”与数学：跨越时空的共鸣

当我们将东方哲学中的“道”与数学联系起来时，会发现惊人的思想共鸣。

“道”在传统理解中，是宇宙万物的本源、规律和运行方式。它“独立不改，周行而不殆”，是“先天而天弗违”的终极法则。这与数学作为“先天科学”的定位何其相似？

“道生一，一生二，二生三，三生万物”的生成逻辑，与数学公理系统如何推导出复杂定理的结构，在形式上高度相似。

5.2 宋明理学的“理”与数学的“结构”

宋明理学提出了“理一分殊”的思想：“太极”（总法则）散为“万理”（具体事物的规律）。每一个具体事物都有其特殊的“理”，但这些特殊的“理”都统一于总的“太极”之中。

数学可以理解为最纯粹、最抽象的“理”。不同的数学分支（代数、几何、分析）研究不同的结构，但它们共享着更深层的逻辑统一性（如范畴论试图揭示的）。

5.3 永恒的“道”与永恒的“数学”

“道”是永恒不变的规则，而现象世界是永恒变化的。“变化是永远不变的”——赫拉克利特的名言在此获得新的意义。

数学作为“道”的理性表达，正是那永恒不变的形式框架。它不随宇宙的演化和人类的兴衰而改变。勾股定理在古希腊成立，在今天成立，在未来无数年后依然成立，即使那时可能已没有人类来理解它。

搜索关键词：道家思想 数学 宋明理学 理一分殊 永恒真理

六、数学的本质：发现还是发明？

6.1 柏拉图主义的强有力证据

许多数学家都描述过类似的体验：感觉自己不是在“创造”数学，而是在“发现”一个早已存在的领域。哥德尔、彭罗斯等顶尖思想家都是坚定的柏拉图主义者。

支持柏拉图主义的主要证据包括：

1. 数学的客观强制性：我们无法随意“发明”数学。1+1必须等于2，圆的周长与直径之比必须是π。数学探索受到极强的内在约束。

2. 数学的预先存在：如前所述，许多数学结构在物理应用之前很久就被发现。

3. 数学的统一性：不同的数学家独立工作，最终会到达相同或等价的数学结构。

6.2 反对声音与回应

反对柏拉图主义的主要论点包括：

• 如果数学客观存在，为何有多种几何（欧氏、非欧）？

• 如果数学是发现的，为何需要人类的创造性工作？

对此，柏拉图主义者可以回应：

1. 数学实在是一个无限丰富的“国度”，不同的几何是这一国度的不同“区域”，它们都是客观存在的数学可能性。

2. “发现”不等于“容易找到”。探索数学需要巨大的创造性，就像探索物理世界（如深海、太空）也需要创造性工具和方法。

6.3 一个综合的视角：主客共舞

或许最合理的观点不是非此即彼，而是认识到：人类心智的理性结构与宇宙的深层数学结构是同构的。

数学既不是纯粹客观的“发现”，也不是纯粹主观的“发明”。它是客观的数学领域与主观的理性能力相遇的场所。我们之所以能发现数学，因为我们的理性与数学实在“匹配”；数学之所以有效，因为宇宙本身具有数学结构。

这种“主客共舞”的观点，既承认了数学的客观性，也肯定了人类理性的创造性参与。

七、数学：宇宙的无声语言与先天代码

7.1 作为“无声语言”的数学

数学是宇宙“诉说”自身结构的语言，但它是无声的——不通过声音或符号直接表达，而是内嵌于万物的关系与模式之中：

• 行星轨道是椭圆方程的物理实现

• 蜂巢结构是最优空间填充问题的自然解

• DNA双螺旋的几何是数学旋转对称性的体现

• 量子世界的概率幅是复数波函数的物理表现

“阅读”这种语言，就是理解宇宙的深层结构。而有趣的是，如果有外星文明，数学将是我们与它们沟通的第一语言，因为它描述的是非人格化的普遍结构关系。

7.2 作为“先天代码”的数学

比“语言”更根本的是“代码”。代码决定了一个系统能做什么、如何运行：

• 先天代码：在系统运行之前就已存在，定义了所有可能性

• 生成性代码：简洁的代码可以生成极其复杂的现象

• 确定性代码：给定初始条件和代码，系统的演化是完全确定的（量子力学的不确定性本质也是由数学规则描述的）

如果宇宙是一台巨大的计算机，那么数学就是它的操作系统和源代码。物理学定律是这部代码运行时的宏观表现。科学家的工作，本质上是逆向工程宇宙的源代码。

7.3 语言与代码的统一

这两个隐喻共同描绘了一个更完整的图景：

• 语言是代码的输出：我们观测到的规律（自然定律）是底层数学代码运行的“可读输出”

• 代码是语言的深层语法：我们之所以能“读懂”宇宙，因为我们的理性与宇宙共享同一套底层代码

这种观点下，数学不再是描述世界的工具，而是世界的本质。追求对宇宙的理解，最终就是去聆听那无声的语言，破译那先天的代码。

八、人类的角色：有限理性者的崇高使命

8.1 数学的绝对性与人类的有限性

数学真理具有一种令人敬畏的绝对性：

• 永恒性：不随时间改变

• 普遍性：不随空间改变

• 必然性：不容许例外

相比之下，人类是有限、短暂、依赖感官的生物。但正是这样的生物，却能够通过理性触及这种非时间性的绝对。这是人类认知的“悲剧性超越”——我们知道自己的有限，却能够理解无限；我们生命短暂，却能思考永恒。

8.2 不断发现：永无止境的探索

“道是永恒不变的规则，变化是永远不变的，就是不断的发现数学之道。”

这句话精妙地捕捉了人类认知的辩证过程：

1. 永恒的道（不变的数学规则）是探索的目标

2. 永恒的变化（现象世界的流变）是探索的背景

3. 不断的发现（人类的认知过程）是连接二者的桥梁

我们永远在“路上”，永远在“逼近”，永远在“发现”。这不是一种缺陷，而是认知的本质——有限者理解无限的唯一方式。

8.3 宇宙的自我意识？

一个更激进的思想是：人类（及其他可能的理性存在）对数学的探索，可能是宇宙自我认识的途径。

如果宇宙本质上是数学结构，而人类理性能够理解这些结构，那么人类对数学的发现，或许可以视为：宇宙通过我们这部分具有反思能力的复杂系统，在时间中逐步认识自身的本质。

这不是神秘主义，而是基于宇宙同构性的合理推断。我们不是宇宙的“外来观察者”，而是宇宙自我观察的“眼睛”。

九、数学在现代与未来的意义

9.1 人工智能时代的数学

在人工智能迅猛发展的今天，数学的基础地位更加凸显：

• 机器学习本质上是高维空间中的优化问题

• 神经网络是复杂函数的近似器

• 算法理论决定了AI能力的根本极限

不理解数学，就不可能真正理解AI的能力与局限。数学不仅是描述世界的语言，也是创造智能的工具。

9.2 数学教育与思维培养

在实用主义盛行的时代，数学教育常被简化为“解题技巧”。但数学的真正价值远不止于此：

• 逻辑思维的训练

• 抽象能力的培养

• 对确定性的追求

• 对错误的诚实面对

这些品质，在信息过载、真假难辨的当代社会，比任何时候都更为重要。

9.3 数学与人类未来

面对气候变化、流行病、能源危机等全球性挑战，数学提供的建模、预测和优化工具不可或缺。但更重要的是，数学所代表的理性精神——尊重事实、尊重逻辑、追求真理——可能是人类应对复杂挑战的最宝贵资源。

十、结论：回归最初的命题

让我们回到开篇的命题：“数学，既不是科学，也不是哲学，他是科学和哲学之母，是先天科学，是先天哲学，是道的规则之因果逻辑。”

经过漫长的思想旅程，我们现在可以更深刻地理解这一命题：

数学是“科学之母”，因为没有数学，科学将无法获得其精确性、预测力和统一性。科学理论必须最终坐落在数学的土壤上。

数学是“哲学之母”，因为数学为哲学提供了理性思维的终极典范，同时也是哲学反思自身能力的最重要镜鉴。

数学是“先天科学”，因为它提供独立于经验的知识框架；数学是“先天哲学”，因为它揭示了理性本身的结构。

数学是“道的规则之因果逻辑”，因为它是宇宙运行最纯粹的形式表达，是那不可言说的“道”在理性范畴内最清晰的呈现。

最终，数学是什么？

数学是理性与存在的交汇点，是可能性与必然性的编织网，是永恒与变化的连接桥。它是人类有限的理性触碰宇宙无限奥秘的唯一可靠途径。

我们每一次证明定理、每一次建立理论、每一次用数学解开自然之谜，都是在变化的洪流中，打下通向永恒彼岸的桩基。数学，就是那根植于永恒、指引我们穿越时间之河的、最可靠的绳索。

而这一切的起点，就是认识到数学的独特地位——它不是科学的仆人，不是哲学的工具，而是孕育它们的母亲，是理解一切的起点，是宇宙写给理性存在者的、最深刻的情书。

【#思考的力量 #理性精神 #知识探索 #人类认知 #宇宙奥秘】

【文章结束】

作者注：本文试图融合东西方思想、科学与哲学、传统智慧与现代认知，探讨数学的根本地位。文中观点部分基于现有哲学和科学理论，部分为思辨性延伸，旨在激发思考而非提供定论。欢迎理性讨论与批评指正。

转发建议：如果你曾被数学的美震撼，如果你思考过知识的本质，如果你对宇宙的奥秘感到好奇，请分享这篇文章。让我们一起重新思考数学——这门既古老又年轻，既抽象又具体，既“无用”又无处不在的学科。