期刊图片复现|Python绘制高颜值Mantel检验网络图+相关性热图
- 2026-02-07 20:17:28
期刊图片复现|Python绘制高颜值Mantel检验网络图+相关性热图

论文:Navigating the safe and just operating space for urban systems: A cross-scale landscape approach 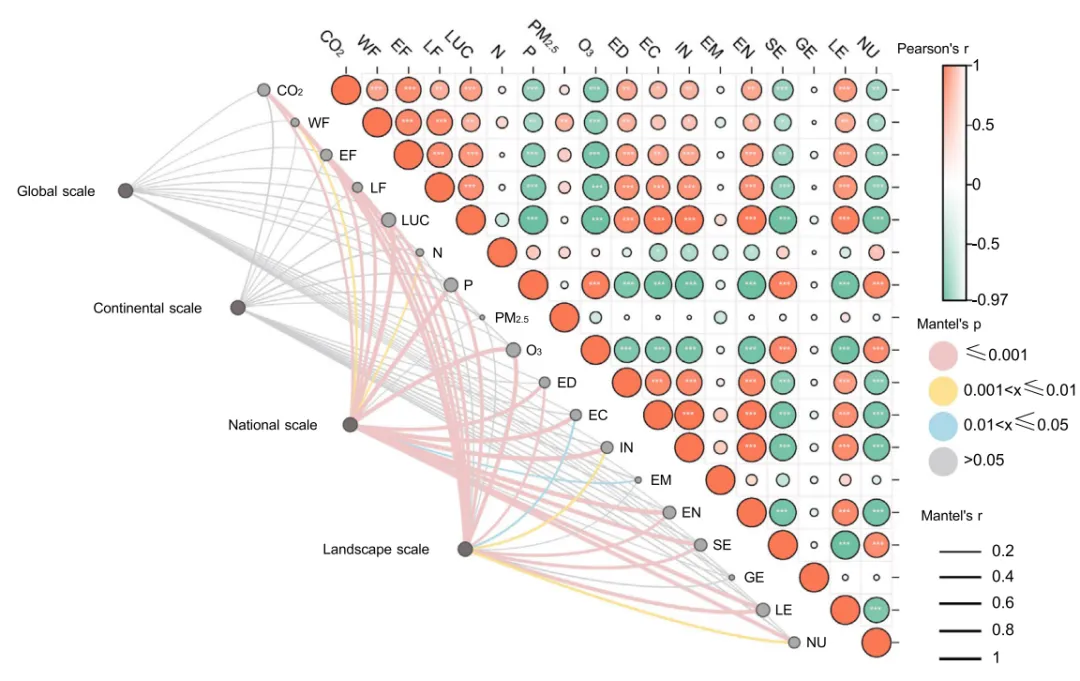
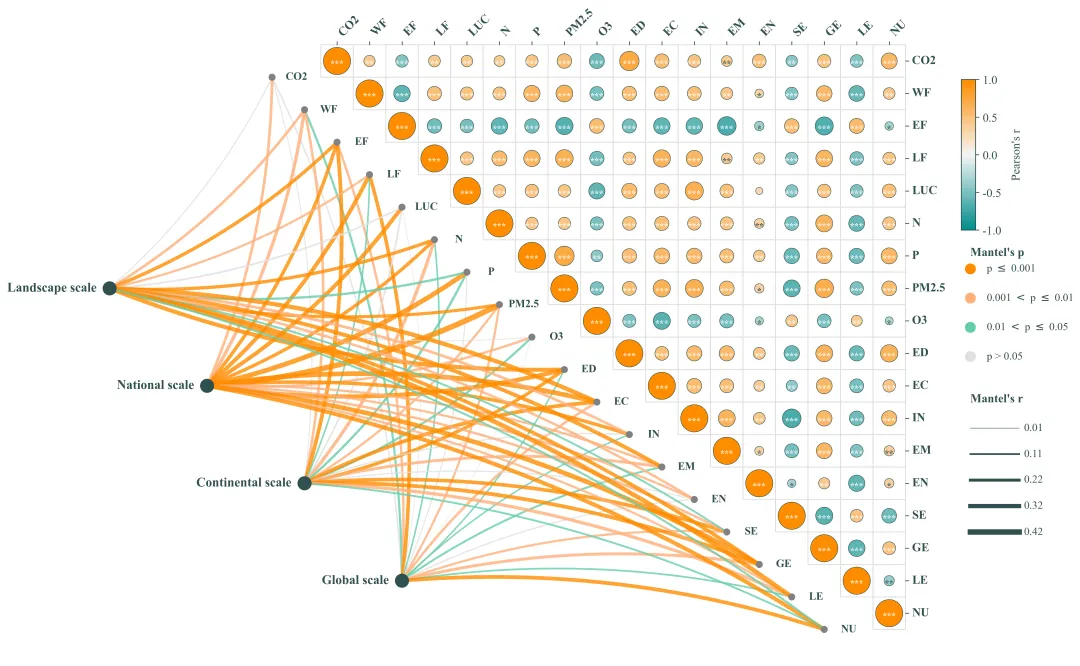
多种配色 此图综合展示了四个空间尺度上的驱动因素与SJOS各项指标之间的跨尺度相互作用及内部关联机制 。图中左侧的网络连线部分代表Mantel检验的结果,连接了左侧的四个尺度节点与中间对角线上的具体SJOS指标,连线的颜色表示统计显著性,连线的粗细则代表Mantel相关系数r的大小(线条越粗表示该尺度对该指标的影响越强)。图中右侧的三角热图部分展示了城市内部各指标间的皮尔逊相关性,圆圈的颜色反映相关性的方向(红色代表正相关,绿色代表负相关),颜色越深且圆圈越大代表相关性越强,圆圈内的星号表示显著性水平。 注意,此为个人理解,可能存在错误,具体内容还请阅读原文进行理解。 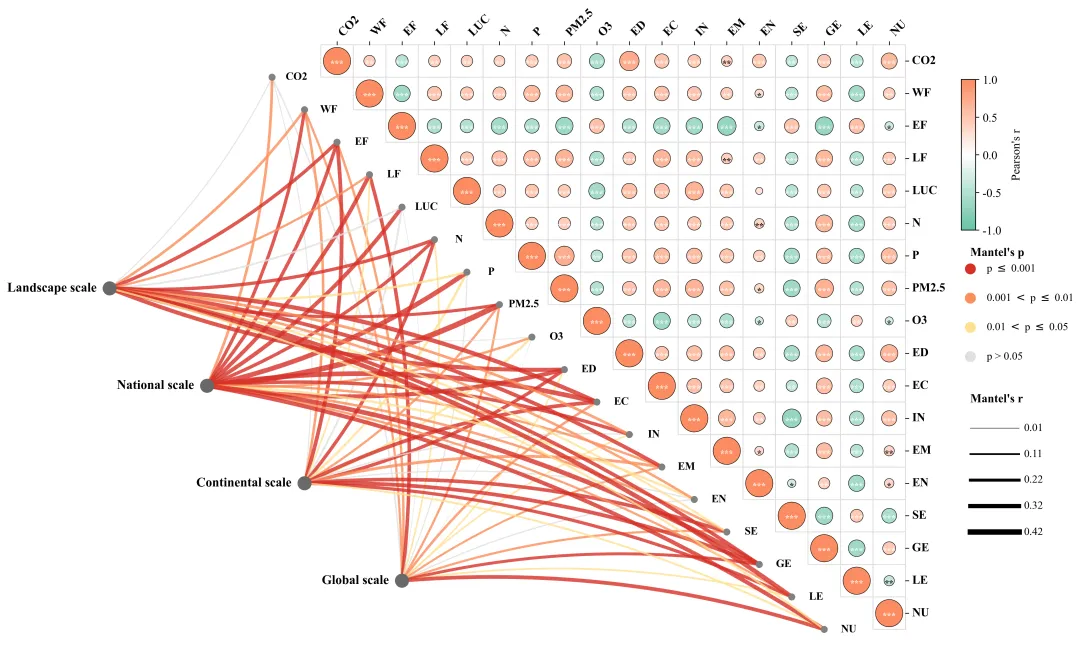
多种配色 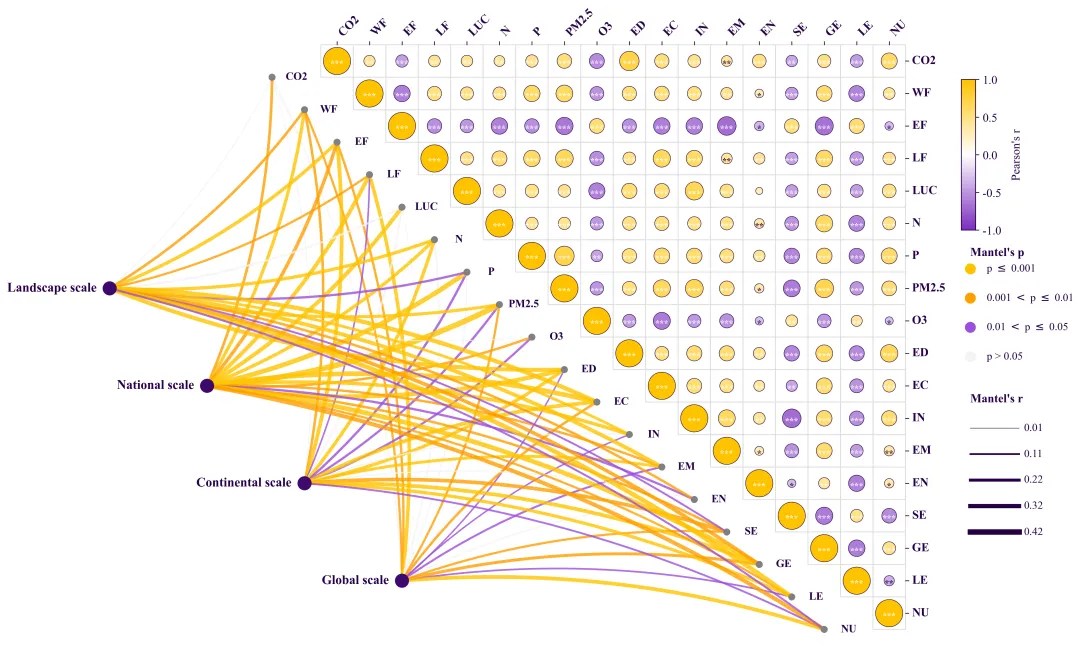
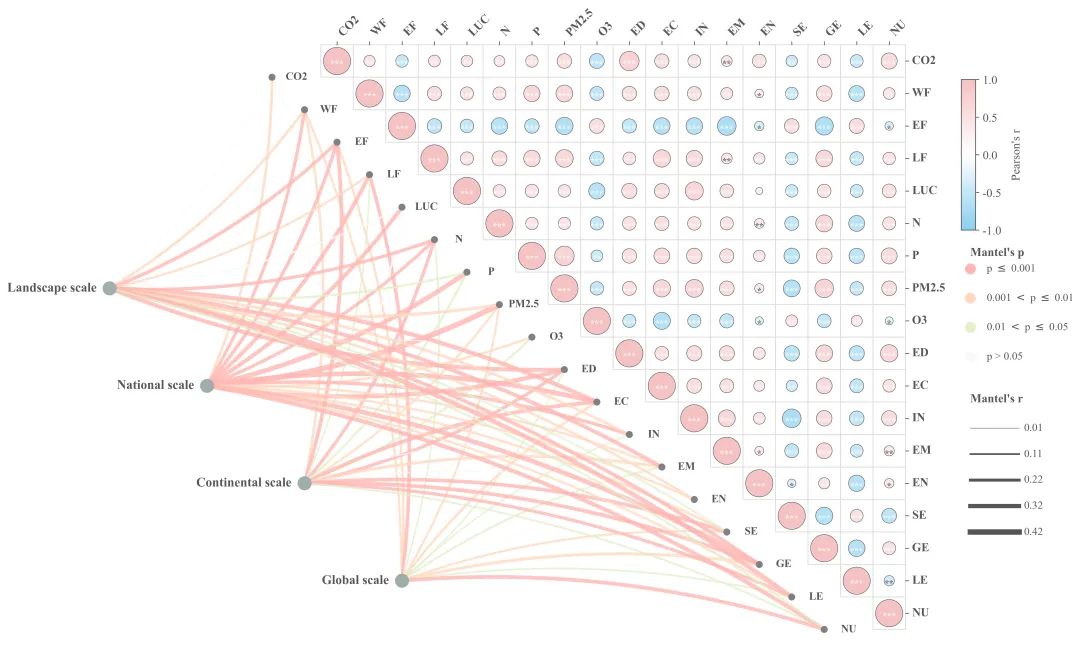
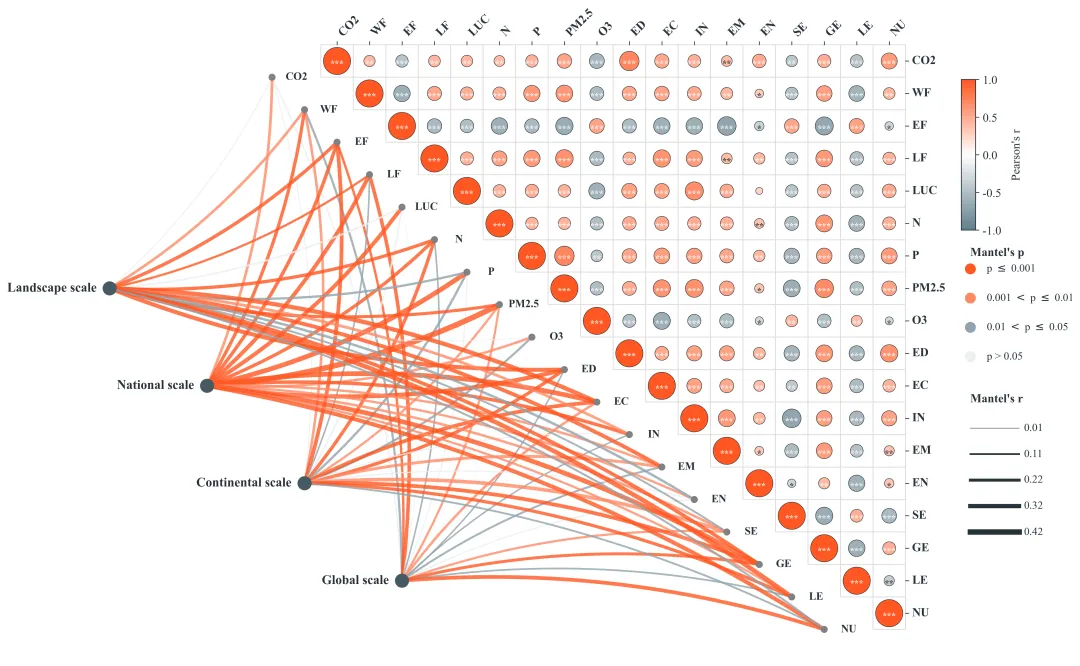
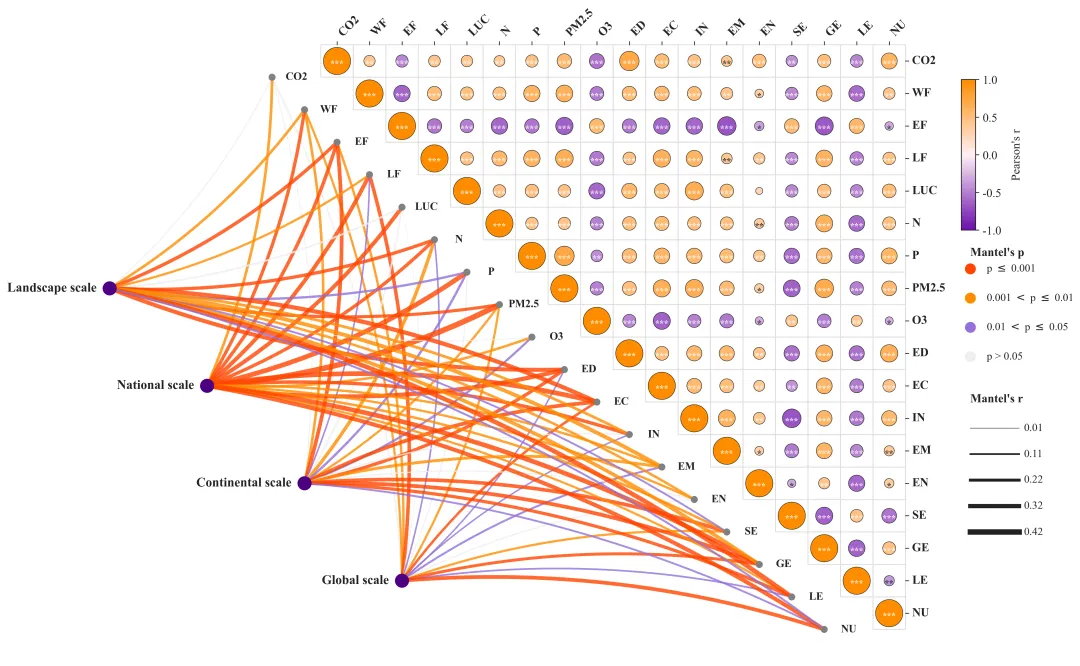
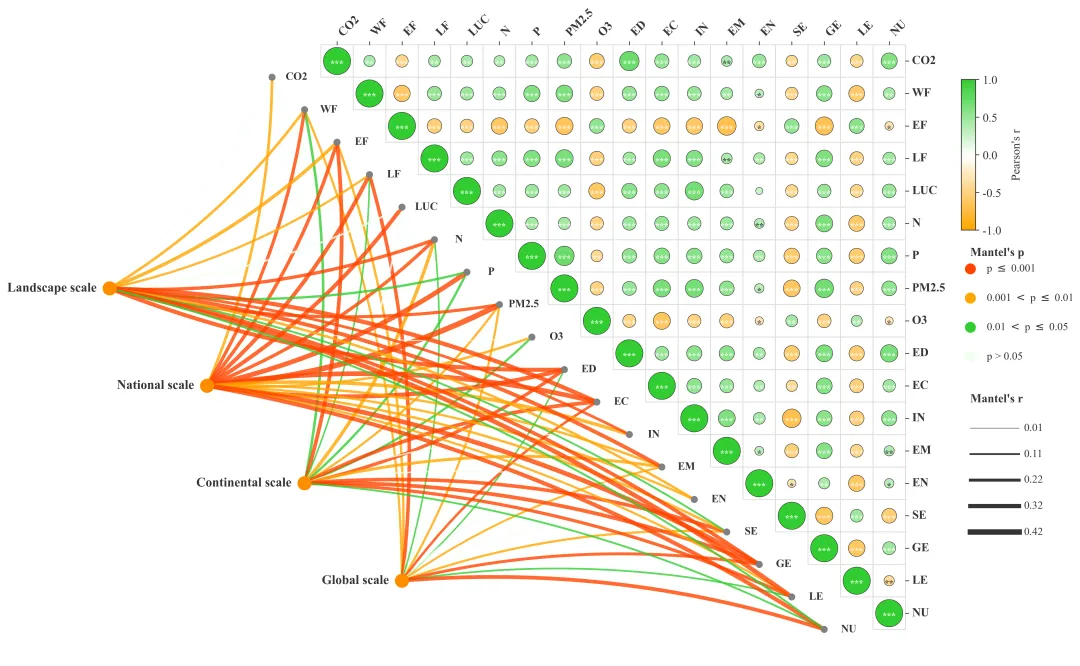
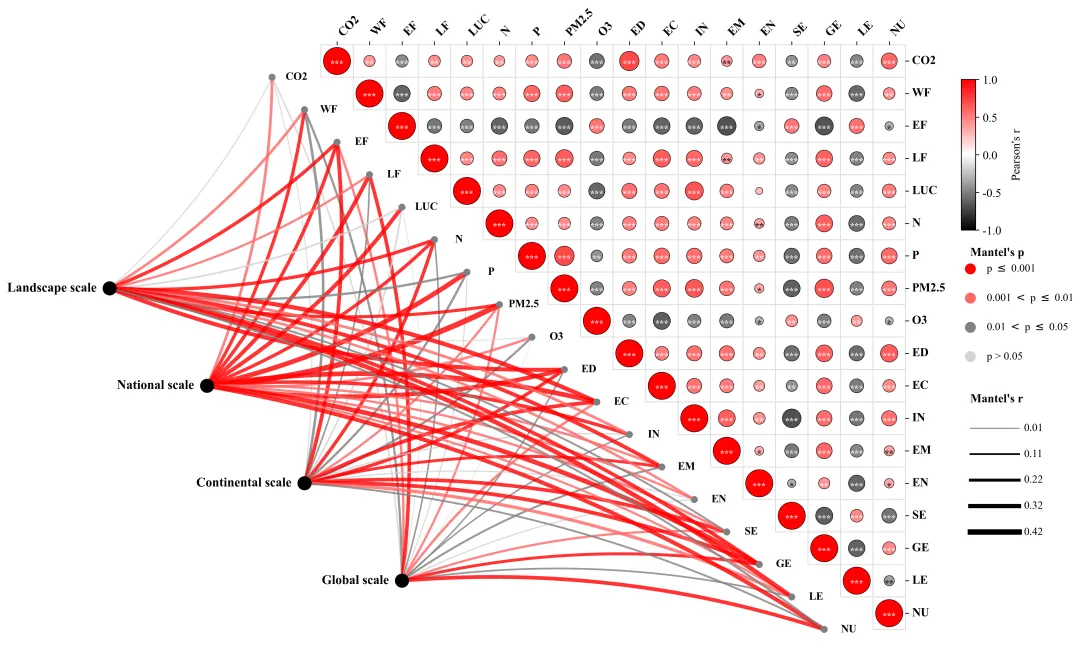
多种配色 



库的导入以及字体设置 

颜色库设置以及配色方案的选择设置 

网络线颜色配置函数,根据 Mantel 检验的显著性 P 值,决定连线的颜色。显著性越高(P值越小),颜色通常越深或越醒目。 

网络线粗细配置函数,将 Mantel 检验的相关系数 R 值(绝对值)映射为线条的粗细。R 值越大,线越粗。 

显著性标记配置函数,将热图中的相关性 P 值转换为星号标记 

绘图函数:初始化画布,提取颜色配置。根据变量数量确定画布布局。创建画布,隐藏坐标轴。定义热图圆点大小和布局间隔。 

绘图函数:绘制右上角的相关性热图,双重循环遍历变量矩阵,确保只绘制右上三角。绘制每个单元格的背景方框。根据相关系数绘制实心圆:如果相关性显著,在圆圈内添加星号。 

绘图函数:在热图的左侧对角线外围,绘制锚点,这些点将作为 Mantel 连线的终点。在锚点和热图之间添加变量名称。在热图的顶部和右侧添加刻度线和倾斜的变量标签。 

绘图函数:绘制左侧的节点,计算左侧大节点坐标位置。通过 

绘图函数:绘制连线,负责画出连接左侧节点和右侧热图锚点的曲线。根据 Mantel 检验结果的P值和 R 值动态设置颜色、粗细。判断线条是向上弯曲还是向下弯曲,避免线条过于密集导致混乱。 

绘图函数:绘制图例以及绘图结果保存 





期刊图片复现|Python绘制二维偏依赖PDP图 期刊复现|python绘制基于SHAP分析和GAM模型拟合的单特征依赖图 期刊图片复现|python绘制带有渐变颜色shap特征重要性组合图(条形图+蜂巢图) 期刊复现|用Python绘制SHAP特征重要性总览图、依赖图、双特征交互效应SHAP图,解锁XGBoost模型的终极奥秘 期刊图片复现|Python绘制shap重要性蜂巢图+单特征依赖图+交互效应强度气泡图+交互效应依赖图(回归+二分类+分类) 

公众号中的所有所有的免费代码都已经下架了,都并入到付费部分里了,付费合集代码和数据的购买通道已经开通,全部合集100元,后续将会持续更新,决定购买请后台私信我,注意只会分享练习数据和代码文件,不会提供答疑服务,代码文件中已经包含了每行代码的完整注释,购买前请确保真的需要!!!

代码绘制成果展示











代码解释


第一部分

# =========================================================================================# ====================================== 1. 环境设置 =======================================# =========================================================================================import matplotlib.pyplot as pltimport numpy as npimport pandas as pdfrom matplotlib.patches import Circle, Rectangle, ConnectionPatchfrom matplotlib.colors import LinearSegmentedColormap, Normalizefrom scipy.spatial.distance import pdist, squareformfrom scipy.stats import pearsonr

第二部分

# =========================================================================================# ======================================2.颜色库=======================================# =========================================================================================COLOR_SCHEMES = {1: {'cmap': ["#66C2A5", "white", "#FC8D62"],'p_colors': {'high': '#D73027', 'med': '#FC8D59', 'low': '#FEE090', 'none': '#E0E0E0'},'node': 'dimgray','text': 'black'},}SCHEME_ID = 18 # 设置当前选用的配色方案config = COLOR_SCHEMES.get(SCHEME_ID, COLOR_SCHEMES[1]) # 获取配色方案cmap = LinearSegmentedColormap.from_list("custom_cmap", config['cmap']) # 根据配置创建自定义的线性渐变色图norm = Normalize(vmin=-1, vmax=1) # 创建归一化对象,将数值映射到 [-1, 1] 范围

第三部分

# =========================================================================================# ======================================3.网络线颜色配置函数=======================================# =========================================================================================def get_mantel_color(p, p_colors):#根据 Mantel 检验的 p 值返回对应的颜色if p <= 0.001:return p_colors['high']if p <= 0.01:return p_colors['med']if p <= 0.05:return p_colors['low']return p_colors['none']

第四部分

# =========================================================================================# ======================================4.网络线粗细配置函数=======================================# =========================================================================================def get_dynamic_width(r, r_min, r_max):#根据相关系数 r 值动态计算线条宽度if r_max <= r_min: # 最大最小值相等return 2.0 # 返回默认宽度val = abs(r) # r的绝对值val = max(r_min, min(val, r_max)) # 限制在最大值、最小值之间normalized = (val - r_min) / (r_max - r_min) # 对数值进行归一化处理return 0.5 + normalized * 5.0 # 将归一化值映射到0.5-5.5的宽度范围

第五部分

# =========================================================================================# ======================================5.显著性标记配置函数=======================================# =========================================================================================def get_sig_label(p):if p <= 0.001:return '***'if p <= 0.01:return '**'if p <= 0.05:return '*'return ''

第六部分

# =========================================================================================# ======================================6.绘图函数=======================================# =========================================================================================def plot_mantel_heatmap(variables, scales, corr_r, corr_p, mantel_df):text_color = config['text'] # 文本颜色node_color = config['node'] #节点颜色p_colors = config['p_colors'] #线颜色n_vars = len(variables) # 右侧热图变量的数量n_scales = len(scales) # 左侧节点的数量# 创建画布fig, ax = plt.subplots(figsize=(18, 14))ax.set_aspect('equal') # 坐标轴比例ax.axis('off') # 关闭坐标轴显示gap_size = 1.5 #、热图和右侧节点之间的间隔base_radius = 0.42 # 设置热图中圆点的基础半径系数anchor_coords = {} # 初始化字典,用于存储左侧变量的连接锚点坐标

第七部分

for i in range(n_vars): # 遍历行变量for j in range(n_vars): # 遍历列变量if j >= i: # 仅绘制对角线及右上方的三角区域grid_x = j # 网格 x 坐标grid_y = (n_vars - 1) - i # 网格 y 坐标# 创建矩形边框rect = Rectangle((grid_x - 0.5, grid_y - 0.5), #坐标1, # 宽度1, # 高度fill=False, # 不填充edgecolor='#E0E0E0', # 边框颜色lw=1, # 线宽zorder=1) # 图层顺序sig_text = get_sig_label(p_val)if sig_text: # 如果有显著性标记star_color = 'white' if abs(r_val) > 0.4 else text_color # 根据背景深浅自动调整星号颜色#添加标记ax.text(grid_x, #xgrid_y - 0.1, #ysig_text, # 文本内容ha='center', # 水平居中va='center', # 垂直居中color=star_color, # 文本颜色fontsize=9, # 字体大小fontweight='bold', # 字体加粗zorder=3) # 图层顺序

第八部分

if i == j: #处理对角线anchor_x = grid_x - 0.5 - gap_size # 连接线锚点的 x 坐标anchor_y = grid_y - 0.5 # 连接线锚点的 y 坐标# 绘制锚点ax.scatter(anchor_x, #xanchor_y,#ys=50, # 点的大小c='gray', # 颜色edgecolors='none', # 无边框zorder=5) # 图层顺序anchor_coords[variables[i]] = (anchor_x, anchor_y) # 存储该变量的锚点坐标# 变量标签的 x 坐标label_x = (anchor_x + (grid_x - 0.5)) / 2# 绘制变量标签文本ax.text(label_x, #xanchor_y,#yvariables[i], # 变量名称ha='center', # 水平居中va='center', # 垂直居中fontsize=11, # 字体大小fontweight='bold', # 字体加粗color=text_color, # 文本颜色zorder=6) # 图层顺序# 绘制变量标签ax.text(right_x + tick_len + 0.1, # x坐标y, # y 坐标var, # 文本内容ha='left', # 水平左对齐va='center', # 垂直居中fontsize=12, # 字体大小fontweight='bold', # 字体加粗color=text_color) # 文本颜色

第九部分

linspace 使其在垂直方向均匀分布,并用 sx = 3-sy 制造了一个倾斜的布局效果。绘制大圆点和对应的文本标签。scale_coords = {} # 初始化字典,存储左侧节点的坐标# 在垂直方向上均匀分布尺度节点的位置scale_y_positions = np.linspace(n_vars -8, 1, n_scales)# 倒序遍历左侧节点名称for idx, name in enumerate(reversed(scales)):sy = scale_y_positions[idx] # y 坐标# 绘制文本ax.text(sx - 0.4, # x 坐标sy, # y 坐标name, # 文本内容ha='right', # 水平右对齐va='center', # 垂直居中fontsize=13, # 字体大小fontweight='bold', # 字体加粗color=text_color) # 文本颜色

第十部分

r_abs_min = mantel_df['r'].abs().min() # Mantel r 值的绝对值最小值r_abs_max = mantel_df['r'].abs().max() # Mantel r 值的绝对值最大值# 如果最大最小值相等if r_abs_min == r_abs_max: r_abs_min = 0# 创建变量名到索引的映射字典var_to_idx = {v: k for k, v in enumerate(variables)}for scale_idx in range(n_scales): # 遍历# 获取当前的所有 Mantel 结果行rows = mantel_df[mantel_df['scale_index'] == scale_idx]rows = rows.copy() # 创建副本rows['var_idx'] = rows['var'].map(var_to_idx) # 映射变量索引rows = rows.sort_values(by='var_idx') # 按变量索引排序# 创建连接线con = ConnectionPatch(xyA=scale_coords[scale_idx], # 起点坐标xyB=anchor_coords[var_name], # 终点坐标coordsA="data", # 坐标系类型coordsB="data",axesA=ax, # 所属坐标轴axesB=ax,arrowstyle="-", # 箭头样式connectionstyle=f"arc3,rad={current_rad}",color=color, # 线条颜色linewidth=lw, # 线条宽度alpha=0.8, # 透明度zorder=4 # 图层顺序)ax.add_patch(con) # 添加连接线到坐标轴

第十一部分

legend_left = n_vars + 3 # 设置图例左边缘的 x 坐标# 添加颜色条的子坐标轴cax = fig.add_axes([0.82, # 左0.60,# 下0.011,# 宽0.15])# 高# 创建颜色条cb = plt.colorbar(plt.cm.ScalarMappable(norm=norm, cmap=cmap),cax=cax)# 颜色条标题cb.set_label("Pearson's r",fontsize=12,labelpad=10,color=text_color)# 设置颜色条刻度参数cb.ax.yaxis.set_tick_params(color=text_color, labelcolor=text_color)cb.outline.set_edgecolor(text_color) # 颜色条边框颜色# 遍历 p 值图例项for label, color in [('p <= 0.001', p_colors['high']),('0.001 < p <= 0.01', p_colors['med']),('0.01 < p <= 0.05', p_colors['low']),('p > 0.05', p_colors['none'])]:# 网络线颜色图例圆点ax.scatter(legend_left-1.5, #xp_legend_y,#ys=120,#大小c=color,#颜色edgecolors='none')#不要边缘线# 绘制图例文字ax.text(legend_left -1, #xp_legend_y,#ylabel.replace('<=', r'$\leq$').replace('<', '$<$'), #文本va='center', # 垂直居中fontsize=11,#大小color=text_color)#颜色# 绘制文本ax.text(legend_left +0.15, #xr_legend_y,#y"{:.2f}".format(r_val), # 文本va='center', # 垂直居中fontsize=11,#大小color=text_color)#颜色r_legend_y -= 0.8 # 向下移动坐标

第十二部分

主程序:数据处理与计算,程序的入口,负责读取数据、执行统计检验并调用绘图函数。
数据读取:从 Excel 读取原始数据。通过切片提取分割数据。
标准化:对所有数据进行 Z-score 标准化,这是计算euclidean距离矩阵前的必要步骤,以消除量纲影响。
Mantel 检验循环:计算两个向量的欧几里得距离矩阵,使用 Spearman 方法进行 Mantel 相关性检验,置换次数 9999 次,将结果存入 mantel_df。
Pearson 相关性:计算变量两两之间的相关系数及其 P 值,用于绘制三角热图。
绘图:调用 plot_mantel_heatmap 进行可视化。将 Mantel 结果、Pearson R 值矩阵、Pearson P 值矩阵保存到新的 Excel 文件中,便于后续查看具体数值。
# =========================================================================================# ======================================2.颜色库=======================================# =========================================================================================if __name__ == "__main__":target_file = r'data.xlsx' #输入数据var_slice_obj = slice(0, 18) # 变量数据scale_slice_obj = slice(18, 22) # 目标数据df = pd.read_excel(target_file, sheet_name=0) # 读取df_vars = df.iloc[:, var_slice_obj] # 获取变量数据df_scales = df.iloc[:, scale_slice_obj] # 获取目标数据variables = df_vars.columns.tolist() # 获取变量名称scales = df_scales.columns.tolist() # 获取目标名称# 实例化标准化器scaler = StandardScaler()# 对变量数据标准化,并转回 DataFrame (保持列名和索引,方便后续 corr 计算)df_vars_std = pd.DataFrame(scaler.fit_transform(df_vars),columns=df_vars.columns,index=df_vars.index)# 对尺度数据标准化,并转回 DataFramedf_scales_std = pd.DataFrame(scaler.fit_transform(df_scales),columns=df_scales.columns,index=df_scales.index)left_data = df_vars_std.values # 获取变量数据的 numpy 数组right_data = df_scales_std.values # 获取目标数据的 numpy 数组n_left = left_data.shape[1] # 获取右侧变量数量n_right = right_data.shape[1] # 获取左侧目标数量mantel_r = np.zeros((n_left, n_right)) # 初始化存储 Mantel r 值的零矩阵mantel_p = np.zeros((n_left, n_right)) # 初始化存储 Mantel p 值的零矩阵mantel_df = pd.DataFrame(mantel_results_list) # 将结果列表转换为 DataFramecorr_matrix = df_vars.corr(method='pearson') # 计算右侧变量间的皮尔逊相关系数矩阵corr_r = corr_matrix.values # 获取相关系数数值矩阵corr_p_matrix = np.zeros((n_left, n_left)) # 初始化相关系数 p 值矩阵df_corr_p = pd.DataFrame(corr_p_matrix, index=variables, columns=variables)with pd.ExcelWriter(output_excel_path, engine='openpyxl') as writer:# Mantel Testmantel_df.to_excel(writer, sheet_name='Mantel_Results', index=False)# 变量间相关系数corr_matrix.to_excel(writer, sheet_name='Pearson_R_Matrix')#变量间相关性显著性df_corr_p.to_excel(writer, sheet_name='Pearson_P_Matrix')

如何应用到你自己的数据

1.设置颜色方案:
SCHEME_ID = 18 2.设置绘图结果的保存路径:
plt.savefig( fr'theme{SCHEME_ID }.png', dpi=300, bbox_inches='tight')plt.savefig( fr'theme{SCHEME_ID }.pdf', dpi=300, bbox_inches='tight')
3.设置原始数据的路径:
target_file = r'data.xlsx' #输入数据4.提取数据:
var_slice_obj = slice(0, 18) # 变量数据scale_slice_obj = slice(18, 22) # 目标数据
5.设置要计算的距离矩阵,注意原文并非使用这种矩阵,我这是因为数据原因,需要根据实际情况进行修改:
dist_matrix_right = squareform(pdist(var_right_col, metric='euclidean'))6.执行mantel检验:
r, p, _ = mantel(dist_matrix_left, dist_matrix_right, method='spearman', permutations=9999) # 执行 Mantel 检验7.设置分析结果的保存路径:
output_excel_path = r'results.xlsx'
推荐


获取方式

本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。
