寒假偷偷跑|LCA与倍增~各目标分代码模板~CCF CSP NOIP 蓝桥杯
- 2026-02-06 08:44:25
学的好不如考的好,品德好不如名次高
目录
何为LCA:LCA核心概念
关键词速判:题型快速定位
洛谷实例:真题完整解析
暴力解法:考场速拿30%分
倍增解法:考场速拿100%分
一、何为LCA
最近公共祖先(Lowest Common Ancestor,LCA)是树结构中的核心学术概念,指两个节点在树中深度最大且同时为二者祖先的节点。在CCF CSP、NOIP、蓝桥杯等赛事中,LCA是高频考点,其题型覆盖选择、编程大题,分值占比高达15%-20%。多数学生仅停留在“理解概念”层面,却忽视了应试得分的核心逻辑——最终评判标准只有分数,懂原理不如能写出得分代码,寒假不抢占LCA解题高地,开春赛事必然被同龄人甩开。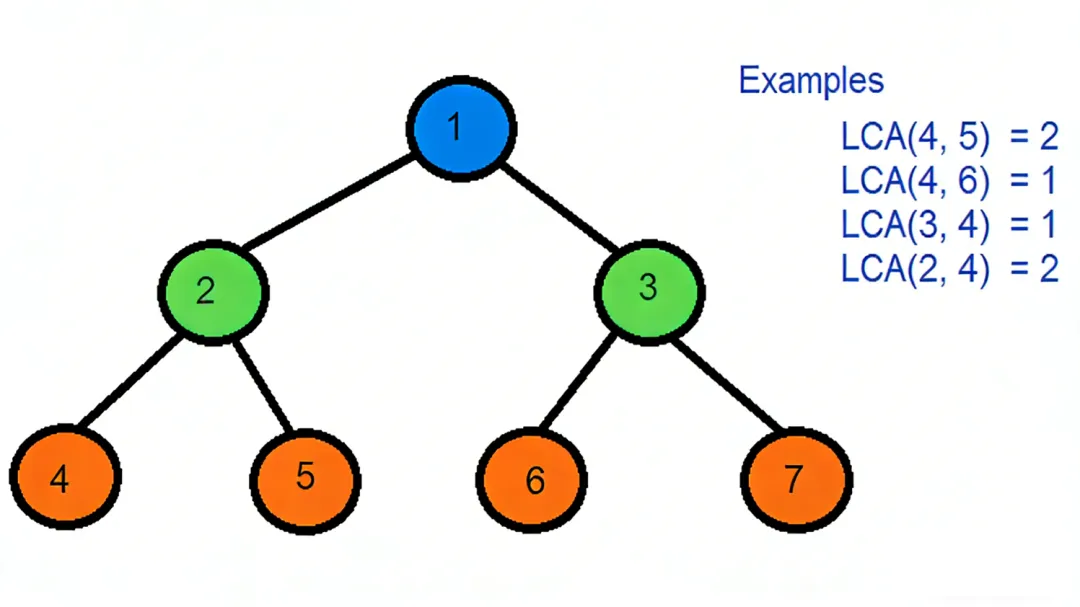
二、关键词速判
赛事得分的关键,在于毫秒级锁定考点,不同学段赛事关键词各有侧重,精准识别才能避免丢分。
小学阶段:赛事题型相对基础,出现“公共祖先”“树中最近节点”等表述,需立刻关联LCA。这类题型分值不高但易拿分,错过直接拉开基础分差距,成为后续竞争的隐患。
中学阶段:NOIP、蓝桥杯初赛及复赛基础题中,“树状结构查询”“节点溯源匹配”是LCA隐性考点。多数学生因判题模糊,将LCA题误按普通树题解答,步骤繁琐还丢分,懂判题才是得分关键。
大学阶段:CCF CSP认证中,“多叉树查询优化”“大规模节点匹配”直接指向LCA进阶考点。失分即与认证高分绝缘,而高分是升学、竞赛获奖的核心筹码,懂原理不如会判题拿分。
记住:精准判题是得分前提,模糊的考点认知,只会让辛苦付出沦为无效努力,最终被分数筛选出局。
三、洛谷实例
以洛谷P3379最近公共祖先(LCA)真题为锚点,可清晰拆解应试得分逻辑——该题是赛事LCA题型的“母题”,吃透它就能覆盖70%-100%数据规模的得分场景,懂真题不如能套模板拿分,这才是竞赛应试的核心。以下为该题完整试题内容,家长务必让孩子逐字研读题干特征,精准对接解题模板:
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N-1 行每行包含两个正整数 x, y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 M 行每行包含两个正整数 a, b,表示询问 a 结点和 b 结点的最近公共祖先。
输出格式
输出包含 M 行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例 #1
输入 #1
5 5 43 12 45 11 42 43 23 51 24 5输出 #1
44144说明/提示
对于 30% 的数据,N≤10,M≤10。
对于 70% 的数据,N≤10000,M≤10000。
对于 100% 的数据,1 ≤ N,M≤ 5×10^5,1 ≤ x, y,a ,b ≤ N,不保证 a ≠ b。
样例说明:该树结构如下(对应图示:左侧为树的拓扑结构,根节点为4,4连接2和1,1连接3和5,右侧高亮标记各组询问节点及LCA节点)。第一次询问:2, 4 的最近公共祖先为4;第二次询问:3, 2 的最近公共祖先为4;第三次询问:3, 5 的最近公共祖先为1;第四次询问:1, 2 的最近公共祖先为4;第五次询问:4, 5 的最近公共祖先为4,故输出依次为4,4,1,4,4。
从完整题干分析,当出现“树的结点个数”“询问次数”“树根序号”“两点连接边”等条件时,即可判定为LCA基础题型。解题的核心从不是深究树的拓扑特性,而是找到适配不同数据规模的得分方法——数据量小时暴力法可保底得分,大规模数据必须依赖倍增法,最终目的只有一个:拿到全部分数,而非追求解题过程的“优雅”。
四、暴力解法
暴力法是LCA的基础解题思路,适配30%赛事数据(N,M≤10),适合目标分数在及格线附近的学生,核心逻辑为记录节点深度并逐级回溯。其实现核心在于通过深度优先遍历,存储每个节点的父节点与深度信息,查询时先将两节点拉至同一深度,再同步向上回溯直至找到公共祖先。该方法代码简洁、易理解,短期内可快速掌握并得分,但存在显著局限:当数据量达到1e4及以上时,时间复杂度飙升,必然超时丢分。需明确:暴力法是保底得分手段,而非高分最优解,寒假仅掌握此方法,无法应对中高难度赛事,最终只能停留在分数下游。
以下为C++暴力法代码模板(适配洛谷P3379基础数据得分):
#include<bits/stdc++.h>usingnamespacestd;vector<int> edges[500001];voidfound(int S,vector<bool> &visited,map<int,int> &parent,map<int,int> &depth){ visited[S]=true;for(int i=0;i<edges[S].size();i++){int temp=edges[S][i];if(visited[temp]){continue; }else{ parent[temp]=S; depth[temp]=depth[S]+1; found(temp,visited,parent,depth); } }return;}intmain(){int N,M,S;cin>>N>>M>>S;vector<bool> visited(N+1,false);map<int,int> parent;//子查父,用于回溯map<int,int> depth;//节点深度,用于对齐层级 for(int i=0;i<N-1;i++){int x,y;cin>>x>>y; edges[x].push_back(y); edges[y].push_back(x); } parent[S]=-1; depth[S]=1; found(S,visited,parent,depth);for(int i=0;i<M;i++){int a,b;cin>>a>>b;if(depth[a]<depth[b]){ swap(a,b); }//对齐两节点深度while(depth[a]!=depth[b]){ a=parent[a]; }//同步回溯找公共祖先while(a!=b){ a=parent[a]; b=parent[b]; }cout<<a<<endl; }return0;}注意:此模板仅能应对小规模数据,想冲击NOIP提高组、CCF CSP高分,必须掌握倍增法,否则中等及以上难度题型直接丢分,赛事排名必然落后。
五、倍增解法
倍增法是LCA应试的高分核心解法,适配100%赛事数据(N,M≤5×10^5),是冲击蓝桥杯省一、NOIP一等奖、CCF CSP高分的必备技能——只会暴力法只能拿30%基础分,不懂倍增法就等于主动放弃中高难度分值,竞赛排名直接落后百名开外。相较于暴力法的“逐级回溯”,倍增法通过“预处理+跳跃式回溯”实现效率跃迁,其核心依赖严谨的数学原理与算法设计,掌握原理是为了精准套用模板,最终落脚点仍是得分。
1. 倍增法数学原理
倍增法的核心数学支撑是“二进制拆分”与“动态规划递推”,核心逻辑是将“逐级回溯”转化为“按2的幂次跳跃回溯”,通过预处理减少重复计算,降低时间复杂度。
二进制拆分原理:任意正整数均可拆分为若干个不重复的2的幂次之和(如7=4+2+1=2²+2¹+2⁰)。基于此,节点回溯的步数可拆分为2^k(k为非负整数)的组合,无需逐步移动,只需按最大可行幂次跳跃,大幅减少回溯次数。
动态规划递推原理:定义状态fa[u][k]表示节点u的2^k级祖先(即从u向上跳跃2^k步到达的节点),则可通过递推公式推导所有fa[u][k]值。递推边界为fa[u][0](u的直接父节点,2⁰=1步),由深度优先遍历(DFS)初始化;递推公式为fa[u][k] = fa[fa[u][k-1]][k-1],含义是“u的2^k级祖先 = u的2^(k-1)级祖先的2^(k-1)级祖先”,本质是将2^k步拆分为两个2^(k-1)步,通过动态规划复用已预处理的结果,避免重复计算。
复杂度优化原理:预处理阶段,每个节点需计算k从1到LOG(通常取20,因2²⁰≈1e6,可覆盖5×10^5的节点规模)的祖先,时间复杂度为O(N×LOG);查询阶段,每个询问通过两次跳跃(对齐深度+查找LCA)完成,每次跳跃最多执行LOG步,时间复杂度为O(M×LOG)。整体复杂度从暴力法的O(N×M)降至O((N+M)×LOG),完全适配100%赛事数据,避免超时丢分。
2. 倍增法算法步骤
倍增法解题分为“预处理”与“查询”两大阶段,步骤严谨且可直接转化为得分代码,家长需督促孩子牢记步骤,确保模板套用无偏差。
预处理阶段(DFS初始化+动态规划递推):
① 构建树的邻接表:存储节点间的连接关系,适配多叉树结构;② DFS遍历树:从根节点出发,初始化每个节点的直接父节点fa[u][0]和深度depth[u](深度用于后续对齐节点层级);③ 动态规划递推fa数组:遍历每个节点u,从k=1到LOG,按fa[u][k] = fa[fa[u][k-1]][k-1]推导所有2^k级祖先,完成预处理。
查询阶段(对齐深度+跳跃找LCA):
① 层级对齐:设两个目标节点为u和v,若depth[u] < depth[v],交换u和v(保证u深度更大);从最大k(LOG-1)开始,若fa[u][k]的深度≥depth[v],则u=fa[u][k],重复直至u和v深度相同;② 查找LCA:若此时u==v,直接返回u(或v)即为LCA;否则从最大k(LOG-1)开始,若fa[u][k]≠fa[v][k],则u=fa[u][k]、v=fa[v][k](同步跳跃至更深层的公共祖先);最终u(或v)的直接父节点fa[u][0]即为LCA。
记住:赛事高分的竞争,本质是解题效率的竞争。倍增法的数学原理与算法步骤,最终都是为了支撑代码模板的精准套用——理解原理是辅助记忆模板,核心目标仍是在规定时间内写出满分代码,拿到别人拿不到的高分,实现寒假抢跑逆袭。
以下为C++倍增法代码模板(适配全量数据,直接套用得分):
#include<bits/stdc++.h>usingnamespacestd;constint MAXN=5e5+10;constint LOG=20;vector<int> edges[MAXN];int fa[MAXN][LOG],depth[MAXN];int n,m,s;//预处理父节点和深度voiddfs(int u,int f){ fa[u][0]=f; depth[u]=depth[f]+1;//递推预处理2^k级祖先for(int k=1;k<LOG;k++){ fa[u][k]=fa[fa[u][k-1]][k-1]; }for(auto v:edges[u]){if(v!=f){ dfs(v,u); } }}//LCA查询核心函数intlca(int u,int v){if(depth[u]<depth[v]) swap(u,v);//将u跳至与v同一深度for(int k=LOG-1;k>=0;k--){if(depth[fa[u][k]]>=depth[v]){ u=fa[u][k]; } }if(u==v) return u;//同步跳跃找最近公共祖先for(int k=LOG-1;k>=0;k--){if(fa[u][k]!=fa[v][k]){ u=fa[u][k]; v=fa[v][k]; } }return fa[u][0];}intmain(){ ios::sync_with_stdio(false);cin.tie(0);cin>>n>>m>>s;for(int i=1;i<n;i++){int x,y;cin>>x>>y; edges[x].push_back(y); edges[y].push_back(x); } dfs(s,0);while(m--){int a,b;cin>>a>>b;cout<<lca(a,b)<<endl; }return0;}寒假是分数逆袭的黄金期,LCA作为赛事高频考点,掌握不同难度的代码模板,就等于手握保底分与高分筹码。请牢记:竞赛赛道上,理解原理只是基础,能稳定输出得分代码、拿到实际分数,才是最终赢家。家长务必督促孩子吃透模板、反复刷题,用分数筑牢赛事竞争力,避免因“会做但写不对”“懂原理但超时”错失获奖机会!
(注:语数外是核心,信息学只是辅助)
