leetcode编程算法随笔(难度1854 Dijkstra )3650. 边反转的最小路径总成本
- 2026-02-04 13:03:10
leetcode编程算法随笔(难度1854 Dijkstra )3650. 边反转的最小路径总成本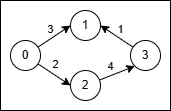
主要包含 思路 1. 首先明确的是,主要是解决图上的最短路径问题,因此点,连接点的边,边的权重,起始点,终点这几个基础是不可少的。变化的情况就具体情况具体分析。 另外,一般情况下,边权非负也很重要,否则无限多的来回走负边,就让问题没有意义了。 2. 从基本点出发,从一个起始点,到一个终点,如果路径有很多,那么一条最短路会有什么特点? 似乎,起点到这个路径上每一个点所选的路径数值都应该是最小的,贪心的感觉就来了~ 假设起点为 s, 终点为 e, 路径 s->...->x->... ->e 是 最短路径 那么 s->...->x 就应该是 s到x的最短路径, 否则,选择一条比当前s到x路径更短的路径,保持x到e 不变,就可以得到一个条更短的路径。 如果所有途径的中间点x 都解决了,是不是有点动态规划的感觉? 3. 如果想,因为路径不确定,所以没法知道哪些点是途径点,似乎问题就卡住了,换方向,换角度 ,这里应该有很多思路,其中一个可能是这样的 假如最短路径为 s-> a -> ... -> x -> .. ->e 那么第一点a 有什么特点? 从 s 到 a 从 a 到 s。。。 a 作为路径上的第一个点,是所有与s 直接相连的点中,路径最短的点吗? 未必啊, 但是呢,如果能发现从s到a的距离也不可能再小了,就会很有用 
#注意边权非负 s不可能通过走其它点,绕路走向a 而是的路径数值更小 #这里似乎很细微,所以看起来也很巧妙,一个词概括:微妙 #可以概括为将比较粗略(抽象)的思路,具体一下,可能会看出点什么~ a与s 放到一起考虑,会如何?它们有什么共同点吗?这很难的样子,但是假如它们是一个整体了,那么新加入的与这个整体距离最近的点,有什么特点? 与前面的a连接到s 一样 新加入的点,无论是与哪个点连入这个整体,从s到它的距离都不能更小了 # 如同动态规划里常常会假定一个状态或者子问题已解决一样。 
在简单的版本里,可以通过遍历,来找到距离当前整体距离最近的点x。 具体做法略。 在优化的版本里,则使用堆。每次加入一个新的点进入整体,就将与该点连接的点遍历一下,加入到堆。比如当a 被加入后,遍历与a相连接的点,加入与原整体相邻元素的堆中,注意度量方式,是与这个整体(集合)的距离。 
#可以总结为,考虑特点的时候,尝试从不同性质,或将该元素放入不同的集合, # 这里好像很有点打哪里指向哪里的感觉!但应该比只是去套公式好一些 到了这一步,基本上就可以写代码了。呃,这个题目,还有个小的弯弯绕,做一些分析,可以知道,还是Dijkstra的方式解决 参考代码 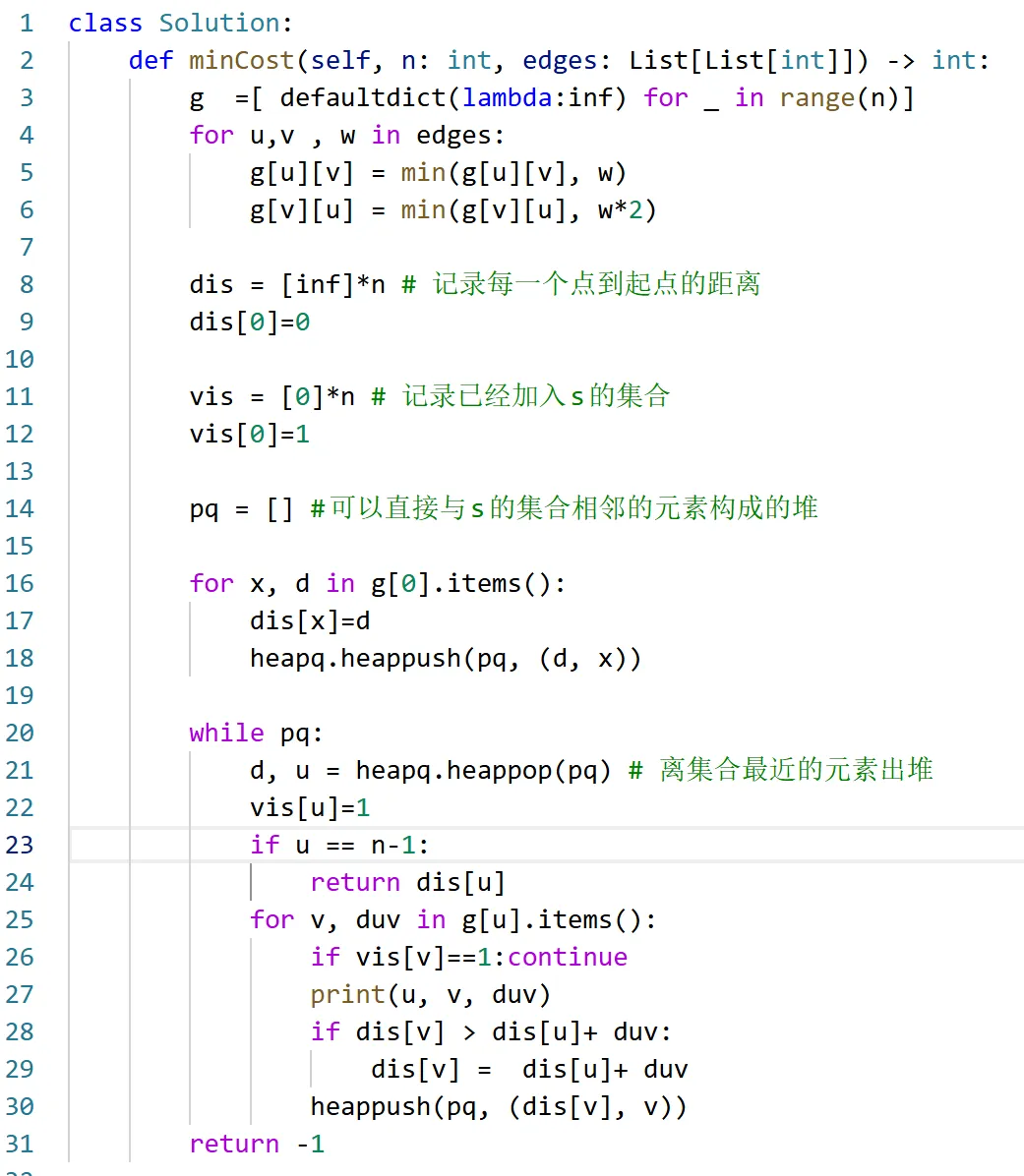
优化也很重要~ 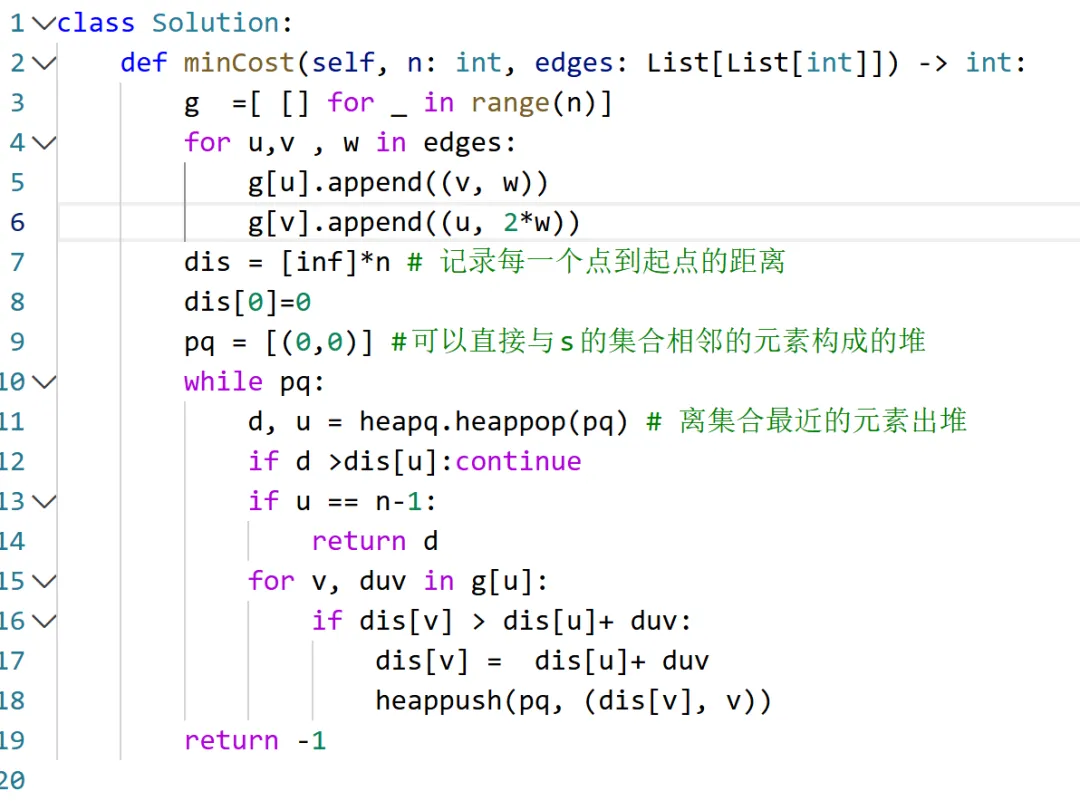
题目
https://leetcode.cn/problems/minimum-cost-path-with-edge-reversals/
给你一个包含 n 个节点的有向带权图,节点编号从 0 到 n - 1。同时给你一个数组 edges,其中 edges[i] = [ui, vi, wi] 表示一条从节点 ui 到节点 vi 的有向边,其成本为 wi。
每个节点 ui 都有一个 最多可使用一次 的开关:当你到达 ui 且尚未使用其开关时,你可以对其一条入边 vi → ui 激活开关,将该边反转为 ui → vi 并 立即 穿过它。
反转仅对那一次移动有效,使用反转边的成本为 2 * wi。
返回从节点 0 到达节点 n - 1 的 最小 总成本。如果无法到达,则返回 -1。
输入:n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]
输出:5
解释:

#一般说D算法的主要思想是以贪心思路解决最短路径(边权和最小最大化)问题
#应试或者刷题的副作用很多,其一就是只记得套公式,却忘记公式的思想和来源以及其启发性, 所以先大概回忆一下Dijkstra算法的大概思路





本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。
