大家好,我是煜道。
今天我们一起来学习 Python基本数据类型(上)——数字类型。
引言
数据类型是编程语言的基础组成部分,它们定义了数据的表示方式、存储空间以及可执行的操作。 Python是一门动态类型语言,其数据类型系统在设计上追求简洁与实用的平衡。理解Python的数据类型,不仅有助于编写正确的代码,更能帮助开发者建立对程序运行机制的深层认知。
在Python中,一切皆为对象(Object)。 这意味着数字、字符串、函数乃至模块,都是具有属性和方法的对象。这一设计使得Python具有高度的一致性,也为元编程提供了基础。
本文将详细探讨Python的数字类型,包括整数(int)、浮点数(float)、复数(complex)以及布尔值(bool)。这些类型构成了Python数值运算的基础,掌握它们是学习更复杂数据结构的前提。
01 Python数字类型概述
Python提供了丰富的数字类型,以满足不同场景下的计算需求:
可以通过type()函数查看变量的类型:
a = 42b = 3.14c = 3 + 4jd = Trueprint(type(a)) # <class 'int'>print(type(b)) # <class 'float'>print(type(c)) # <class 'complex'>print(type(d)) # <class 'bool'>
值得注意的是,bool是int的子类,True和False在数值运算中分别等价于1和0。这一设计虽然提供了便利,但也可能在某些情况下导致意外的结果。
print(True + 1) # 输出:2print(False * 10) # 输出:0
02 整数类型(int)
整数的表示
Python 3中的整数类型int没有长度限制(受限于可用内存),这与C、Java等语言有本质区别。在C语言中,int通常是4字节,取值范围为-2,147,483,648到2,147,483,647;而Python的整数可以任意大。
# 普通十进制整数a = 42b = -7c = 0# 大整数large_number = 10 ** 100# 10的100次方print(large_number) # 10000...000 (共101位)# 十六进制表示(以0x开头)hex_num = 0xFFprint(hex_num) # 255# 八进制表示(以0o开头)oct_num = 0o77print(oct_num) # 63# 二进制表示(以0b开头)bin_num = 0b1010print(bin_num) # 10
整数运算
Python支持标准的算术运算:
a = 10b = 3# 基本运算print(a + b) # 加法:13print(a - b) # 减法:7print(a * b) # 乘法:30print(a / b) # 除法:3.333...(结果为float)print(a // b) # 整除:3print(a % b) # 取余:1print(a ** b) # 幂运算:1000# 负数除法的特殊性print(-10 // 3) # 输出:-4(向下取整)print(-10 % 3) # 输出:2
关于/和//的区别,需要特别注意:
//执行的是整除(地板除),结果向负无穷方向取整。
print(7 / 2) # 3.5(float)print(7 // 2) # 3(int)print(7.0 // 2) # 3.0(float,因为操作数包含float)
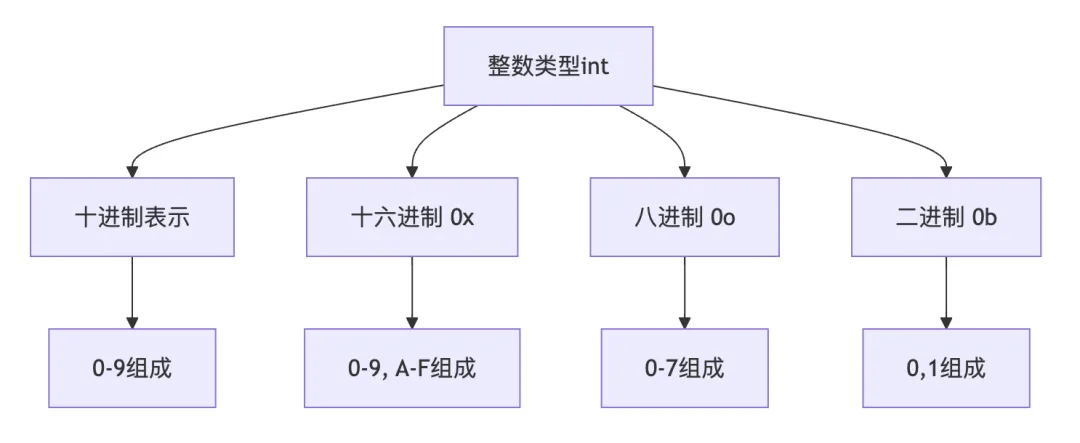
位运算
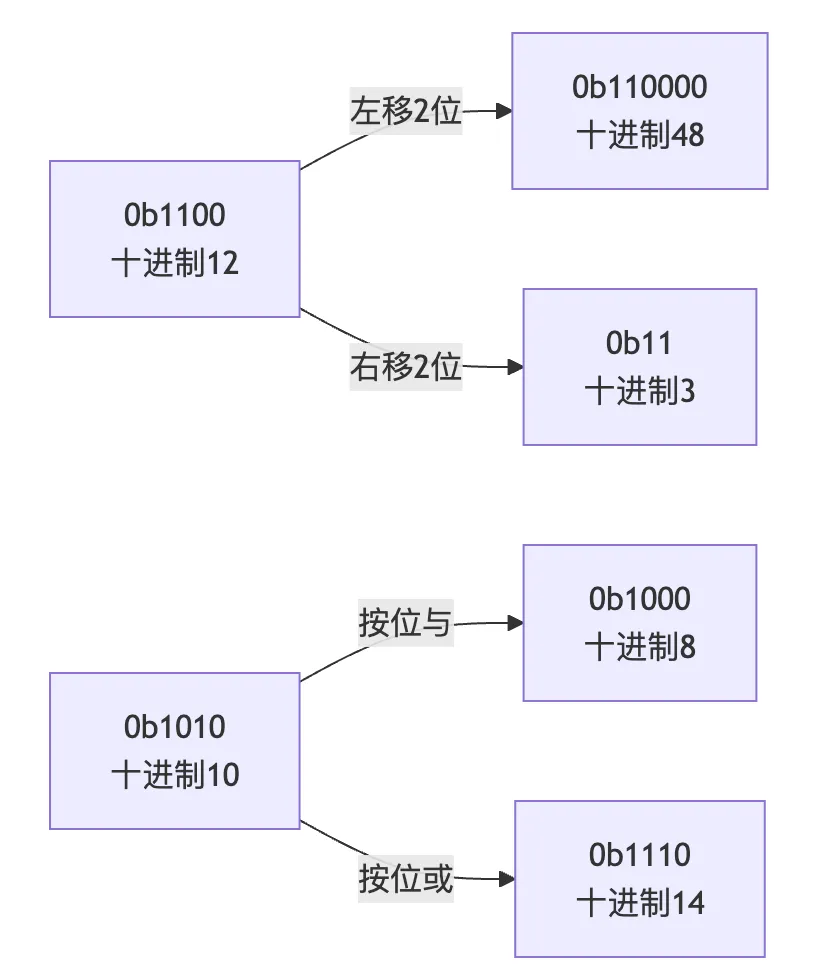
Python的整数类型支持完整的位运算,这在处理底层数据、权限控制、算法实现等场景中非常有用:
x = 0b1100# 12y = 0b1010# 10print(bin(x | y)) # 按位或:0b1110 → 14print(bin(x & y)) # 按位与:0b1000 → 8print(bin(x ^ y)) # 按位异或:0b0110 → 6print(bin(~x)) # 按位取反:-0b1101 → -13# 左移和右移print(x << 2) # 左移2位:48(0b110000)print(x >> 2) # 右移2位:3(0b11)
03 浮点数类型(float)
浮点数的表示
浮点数用于表示实数,是计算机中数值计算的基础。Python的float类型基于IEEE 754双精度标准实现:
# 浮点数表示a = 3.14159b = -0.5c = 1e10# 科学计数法:1 × 10¹⁰d = 1.5e-3# 科学计数法:1.5 × 10⁻³print(type(c)) # <class 'float'>print(c) # 10000000000.0
浮点数的精度问题
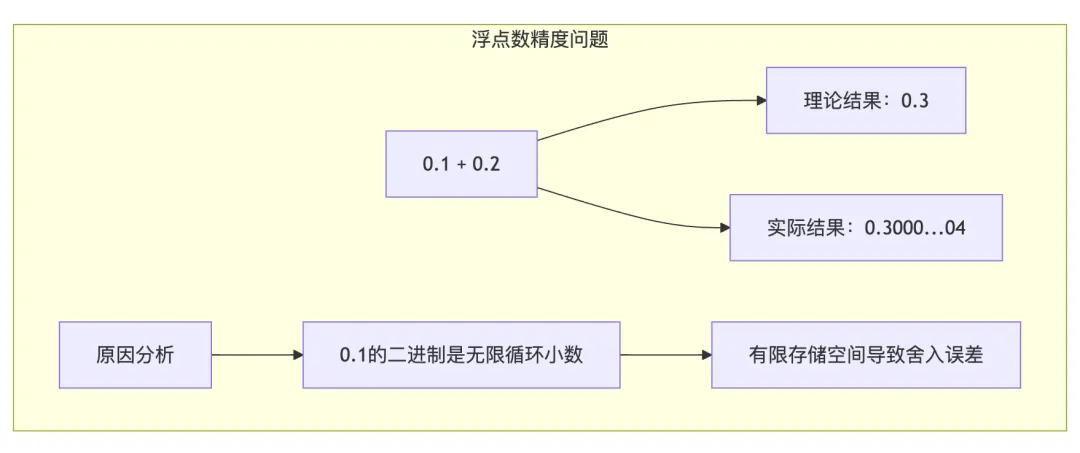
浮点数运算存在精度限制,这是由其二进制表示方式决定的。在十进制下看似简单的运算,可能产生意料之外的结果:
# 经典的浮点数精度问题print(0.1 + 0.2) # 输出:0.30000000000000004print(0.1 * 0.2) # 输出:0.020000000000000004# 验证print(0.1 + 0.2 == 0.3) # 输出:False
这一问题的根源在于:十进制的0.1无法精确表示为二进制浮点数。0.1的二进制表示是一个无限循环小数,在有限的存储空间中必然产生舍入误差。
处理浮点数精度
在实际开发中,有几种方法可以处理浮点数精度问题:
方法一:使用Decimal
decimal模块提供了精确的十进制运算:
from decimal import Decimal, getcontext# 设置精度getcontext().prec = 28# 默认精度a = Decimal('0.1')b = Decimal('0.2')print(a + b) # 输出:0.3print(a * b) # 输出:0.02
方法二:使用整数的"分"单位
在处理货币时,可以先将金额转换为最小单位(分),计算完成后再转换回元:
# 以分为单位进行计算price1 = int(0.1 * 100) # 10分price2 = int(0.2 * 100) # 20分total = (price1 + price2) / 100# 0.3元
方法三:格式化输出
对于只需要展示的场景,可以使用格式化控制输出精度:
result = 0.1 + 0.2print(f"{result:.2f}") # 输出:0.30print(round(result, 2)) # 输出:0.3
特殊浮点值
浮点数系统包含几个特殊值:
# 正无穷和负无穷print(float('inf')) # infprint(float('-inf')) # -inf# NaN(Not a Number)print(float('nan')) # nan# 验证import mathprint(math.isinf(float('inf'))) # Trueprint(math.isnan(float('nan'))) # True# 特殊情况print(float('inf') - float('inf')) # nanprint(float('inf') * 0) # nan
04 复数类型(complex)
复数的表示
Python原生支持复数运算,这在科学计算和工程应用中非常有用:
# 复数表示a = 3 + 4jb = 2 - 1jprint(type(a)) # <class 'complex'>print(a.real) # 实部:3.0print(a.imag) # 虚部:4.0# 复数运算print(a + b) # (5+3j)print(a * b) # (10+5j)print(a / b) # (0.4+2.2j)
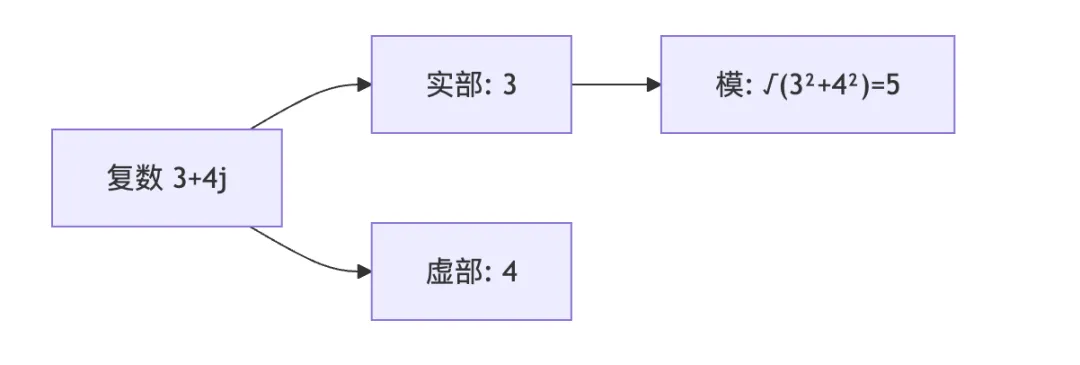
共轭与模
复数对象提供了获取共轭和计算模的方法:
z = 3 + 4j# 共轭复数print(z.conjugate()) # (3-4j)# 模(绝对值)print(abs(z)) # 5.0
05 布尔类型(bool)
布尔值的本质
bool类型是Python中实现逻辑判断的基础。它只有两个取值:True和False。
# 布尔值的创建a = Trueb = Falseprint(type(a)) # <class 'bool'>print(isinstance(a, int)) # True,因为bool是int的子类
布尔值的隐式转换
在Python中,很多类型都可以隐式转换为布尔值。这种转换遵循"真值测试"规则:
# 数值print(bool(0)) # Falseprint(bool(42)) # Trueprint(bool(-3.14)) # True# 字符串print(bool('')) # Falseprint(bool('hello')) # True# 容器print(bool([])) # Falseprint(bool([1, 2, 3])) # Trueprint(bool({})) # Falseprint(bool({'a': 1}))# Noneprint(bool(None)) # False
布尔运算
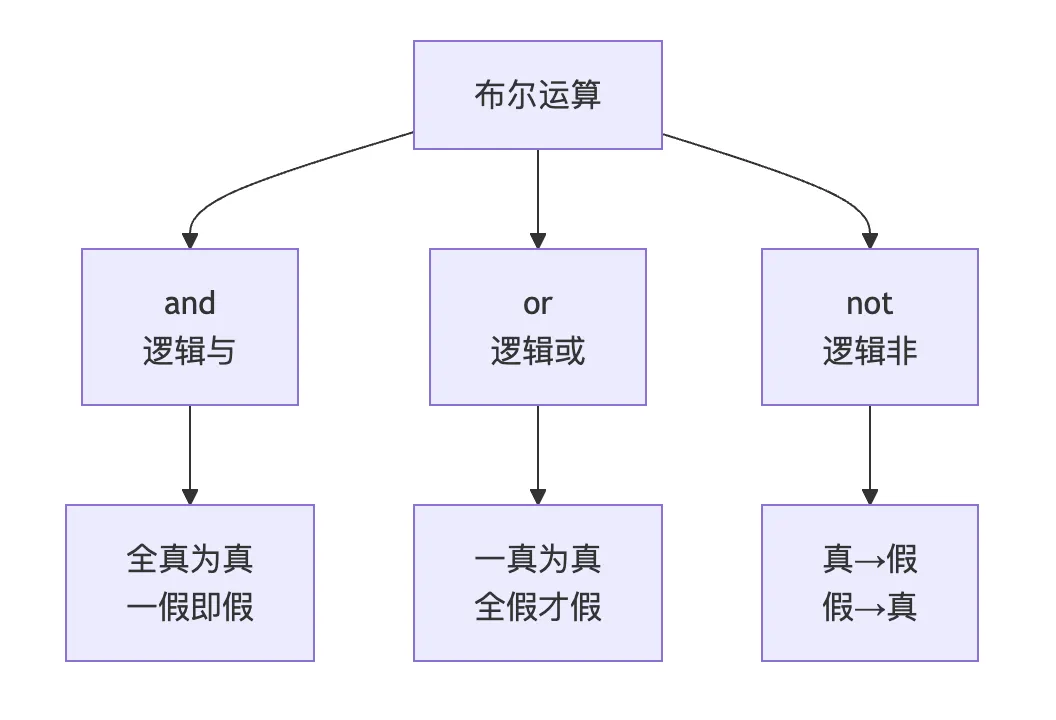
Python提供了三个布尔运算符:and、or和not:
# and:所有操作数都为真时返回真print(TrueandTrue) # Trueprint(TrueandFalse) # Falseprint(FalseandFalse) # False# or:任意一个操作数为真时返回真print(TrueorFalse) # Trueprint(FalseorFalse) # False# not:取反print(notTrue) # Falseprint(notFalse) # True# 短路求值print(0and1) # 0(第一个为False,直接返回)print(1or2) # 1(第一个为True,直接返回)
比较运算符与布尔值
比较运算符的结果总是布尔值:
# 比较运算print(10 > 5) # Trueprint(3 == 3) # Trueprint(2 != 4) # True# 链式比较(Python特有)print(1 < 2 < 3) # Trueprint(1 < 2 > 3) # Falseprint(10 < 20 < 30 < 40) # True# 身份比较a = [1, 2, 3]b = [1, 2, 3]print(a == b) # True(值相等)print(a is b) # False(身份不同)
06 数字类型的相互转换
显式类型转换
Python提供了内置函数进行数字类型之间的转换:
# 整数转浮点数print(float(42)) # 42.0# 浮点数转整数print(int(3.9)) # 3(直接截断)print(int(-3.9)) # -3# 浮点数转整数(四舍五入)print(round(3.5)) # 4print(round(3.4)) # 3# 转布尔值print(bool(0)) # Falseprint(bool(42)) # Trueprint(bool(0.0)) # Falseprint(bool(-3.14)) # True# 任意类型转字符串print(str(42)) # '42'print(str(3.14)) # '3.14'
隐式类型转换
在进行混合类型运算时,Python会自动进行类型提升:
# 整数与浮点数运算print(10 + 3.5) # 13.5(int提升为float)print(10 * 3.0) # 30.0# 整数与布尔值运算print(10 + True) # 11(True提升为1)print(10 * False) # 0(False提升为0)
下表总结了Python的隐式类型提升规则:
| |
|---|
| |
| |
| |
| float → complex,结果为complex |
| |
07 数字类型的高级话题
整数缓存机制
Python对较小的整数进行了缓存(通常在-5到256之间):
a = 100b = 100print(a is b) # True(相同对象)a = 1000b = 1000print(a is b) # 理论:False(不同对象),实际:True(相同对象),代码块优化:在同一代码块中,相同的大整数也会被复用。# 验证缓存范围print(-5is-5) # Trueprint(256is256) # Trueprint(257is257) # 理论:False,实际:True(相同对象),常量折叠:解释器在编译时直接将两个257合并为一个对象。
数字类型的内存布局
Python的数字类型在内存中的表示方式各不相同:
import sys# 各类型的内存占用print(sys.getsizeof(0)) # 28字节(int对象)print(sys.getsizeof(0.0)) # 24字节(float对象)print(sys.getsizeof(True)) # 28字节(bool对象)print(sys.getsizeof(1+2j)) # 32字节(complex对象)# 大整数的内存占用large = 10 ** 100print(sys.getsizeof(large)) # 72字节,大整数占用更多内存
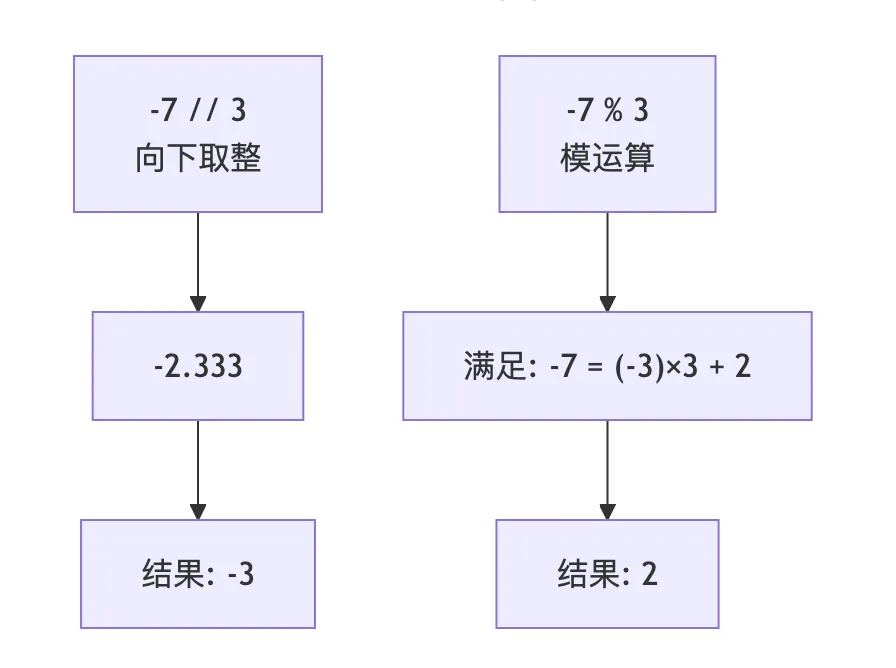
整数除法的取整方向
Python的整除运算符//采用向下取整(floor)策略:
# 正数整除print(7 // 3) # 2# 负数整除(向下取整)print(-7 // 3) # -3(不是-2)# 取模运算print(7 % 3) # 1print(-7 % 3) # 2# 验证:a = (a // b) * b + (a % b)print(7 == (7 // 3) * 3 + (7 % 3)) # Trueprint(-7 == (-7 // 3) * 3 + (-7 % 3)) # True
下表展示了Python整数除法和取模运算的结果:
可以看到,对于负数-7 // 3:
- 地板除结果为-3(因为-2.333向下取整为-3)。
- 取模结果为2(满足:-7 = (-3) * 3 + 2)。
08 小结
本文详细介绍了Python的数字类型,包括整数、浮点数、复数和布尔值。这些类型是Python数值运算的基础,理解它们的特性和限制对于编写正确的程序至关重要。
需要特别注意的是:
- 整数类型
int在Python 3中没有长度限制,但运算效率会随位数增加而下降。 - 浮点数存在精度问题,涉及金融计算时建议使用
decimal模块。 - Python的整除采用向下取整策略,处理负数时需要特别注意。
