I.INTRODUCTION 引言

稀疏的阵列会存在大量的栅瓣，这些栅瓣会导致在角度估计时出现模糊，从而严重影响参数估计性能，因此有大量的文章研究如何抑制阵列的栅瓣，博主在很久之前完全看懂过一篇文章，并且完美复现了出来，最近来做个分享。

该论文提出一种基于双载频方向图相乘的栅瓣抑制算法，并分析了影响栅瓣抑制效果的因素，以峰值旁瓣比作为栅瓣抑制性能的评价指标，对影响该算法的性能频率的频率差关键参数进行定量分析，推导出栅瓣抑制后峰值旁瓣比与频率差以及载频间的最大差异与阵列天线间距关系的表达式。

II.SIGNAL MODEL 信号模型

考虑  个天线组成的发射阵列和  个天线组成的接收阵列构成的均匀稀疏分布的一维分布式MIMO阵列。发射和接收天线之间的间距分别为：，，其中，，分别为发射阵列天线间距系数与接收阵列天线间距系数，， 为载频1对应信号波长。假设目标与阵列的距离远大于阵列孔径，均匀稀疏分布的一维分布式MIMO阵列如图所示。

假定发射天线将基带信号为：

其中， 为  的窄带正交发射基带信号矢量。将  分别调制到频率为  和  的载频上作为发射信号，此时发射信号阵列的发射信号矢量  可表示为：

理想情况下接收天线的接收回波信号矢量  可以表示为：

其中， 为第  个接收天线的接收信号， 为  的接收端噪声向量，， 分别为载频1对应的接收阵列和发射阵列导向矢量，， 分别为载频2对应的接收阵列和发射阵列导向矢量。

我们来分析一下导向矢量的乘积：

同时它的第一行为：

同时它的第二行为：

第  行为：

其中，，， 为载频2对应信号的波长。

将接收的信号  与两个载频的本振  和  混频后,再经过冲激响应为  的低通滤波器分别得到载频1,2对应的接收向量 ,,可表示为：

然后将载频1,2对应的接收向量经过  个匹配滤波器输出矢量 ， 可以表示为（假设正交信号直接理想正交）：

其中：

也即，通过上面一系列的操作，我们得到了最想要的载频1和2对应的MIMO阵列导向矢量。

对载频1,2对应的匹配滤波后结果 ， 分别进行波束形成，得到 ，:

其中，，分别为载频1,2对应的波束形成器的权矢量。

假设期望信号来波方向为 ，载频1,2对应的最优波束权矢量为：

然后可得，载频1,2对应的阵列归一化方向图 ， 分别表示为：

通过上式可知，载频1和2对应的阵列方向图栅瓣出现的位置 ， 分别可以表示为：

其中， 为 ， 的最大公约数。由上式可知,出现栅瓣的数量与天线间距的公约数以及与波长的比值相关,比值越大出现栅瓣的数量越多。

下面我们进行一些仿真来看看，波束指向零度，其他仿真参数如表所示。

通过上面分析可知，载频1栅瓣的位置为：

依次类推，如图所示：

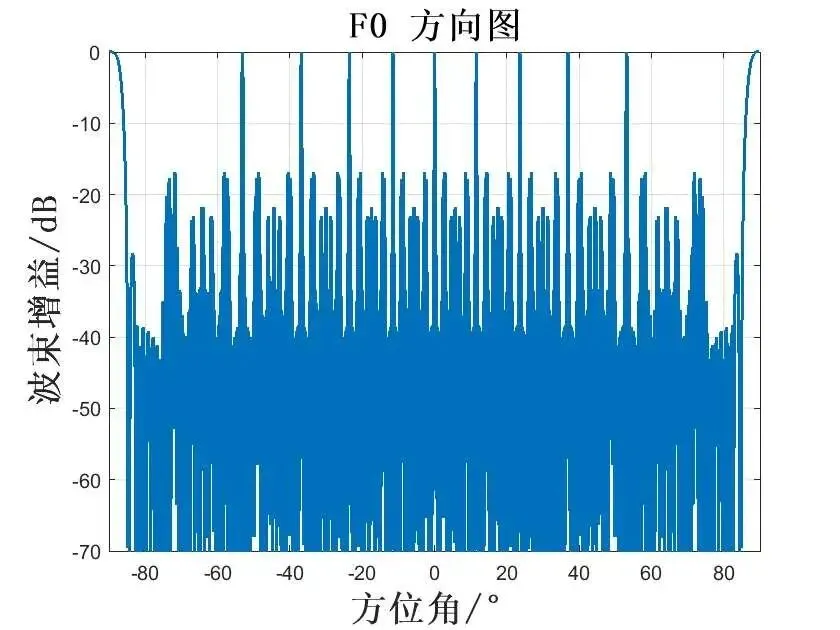
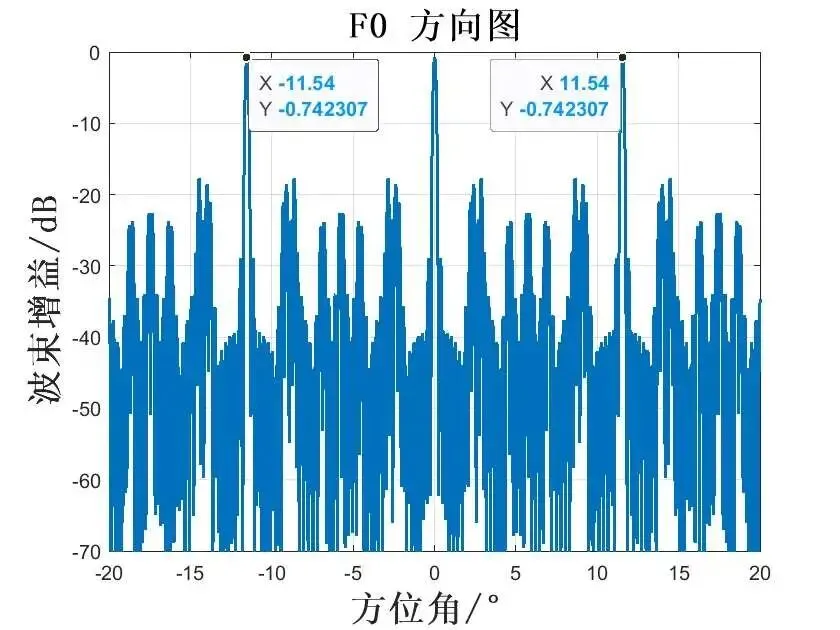
通过上面分析可知，载频2栅瓣的位置为：

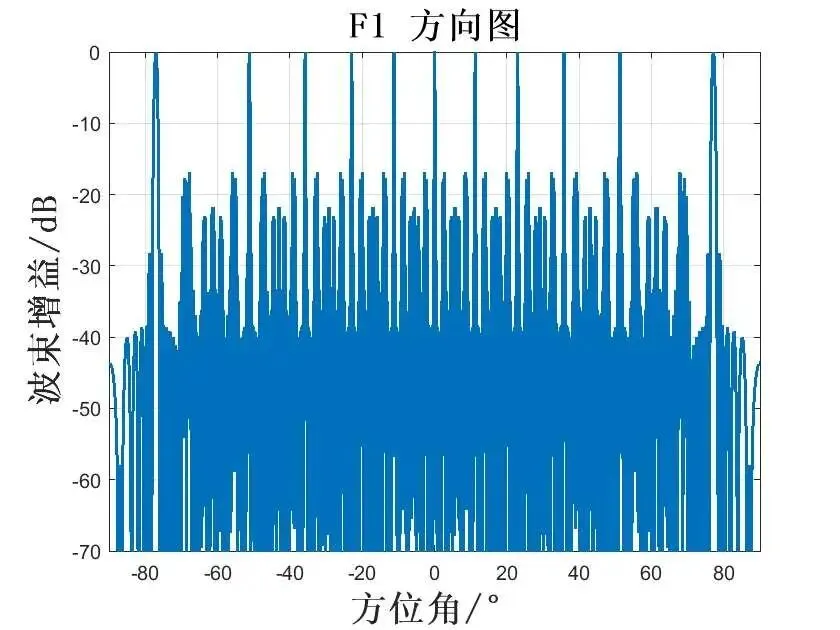
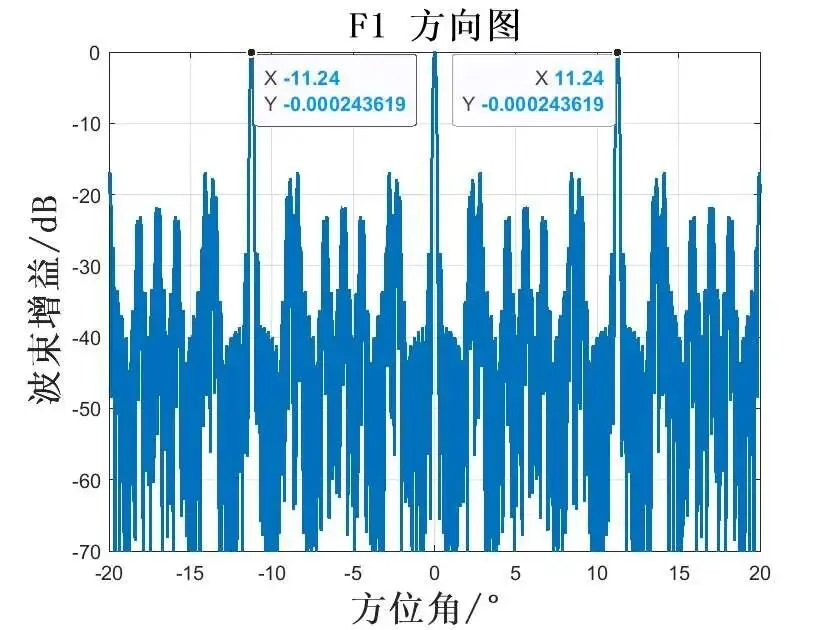
上面的栅瓣位置是估计值，同时由于采样栅栏效应”（Picket Fence Effect）会出现误差。

III.PROPOSED ALGORITHM 基于双载频方向图相乘的栅瓣抑制算法原理

由上式可知,阵列方向图栅瓣出现的位置与信号的载频有关。当阵列的主瓣位置指向一定,两组不同载频信号对应的阵列方向图具备主瓣位置相同但栅瓣位置存在差异的特性,利用该特性将两组不同载频对应的阵列方向图进行相乘处理。两组不同载频对应方向图相乘得到的归一化方向图  可表示为：

由归一化阵列方向图特性可知，对  都有：

那么可以得到：

其中：

当且仅当， 时上式取得最大值1,其余方向幅度相比于载频1,2对应阵列方向图均有不同程度下降,由此达到保留主瓣幅度同时抑制栅瓣幅度的目的。

令：

在这里是为了把  和   引入进来，同时  和   为正整数。同时我们考虑频率差：，我们通过上面的分析可以大致知道，频率差肯定是有范围的，不然栅瓣之前会重合，导致提高频率差并不能提升栅瓣抑制性能。同时定义：

 和  描述的是：“在同一个周期里，发射和接收谁隔得更远”。阵元间距越大，栅瓣出现得越早、越近主瓣、越危险。更稀疏 → 栅瓣更早出现。

为了尽可能避免出现栅瓣重合，我们从最稀疏的阵列出发，同时不考虑MIMO联合起来的  和 ，而是考虑单独发射和接收阵列出现栅瓣的情形。单阵列参数：假设我们只看那个最稀疏的阵列（比如接收阵），它的总间距倍数是：。

重合条件，也即存在整数 ， 使得：

对上式进行一阶泰勒展开可知：

通过上面可以得到重合条件为：

当频率相对偏移量 能被某个小整数比 逼近时，栅瓣就会再次对齐。

避免任何“低阶整数解”存在，最危险的是：，这时：

所以只要保证：

就能彻底避免重合。

通过上面分析可知：

工程上多个保守下界，所以论文里给的是：

也即：

下面通过仿真得到，双载频相乘得到的方向图，可以看到很好的抑制了栅瓣。

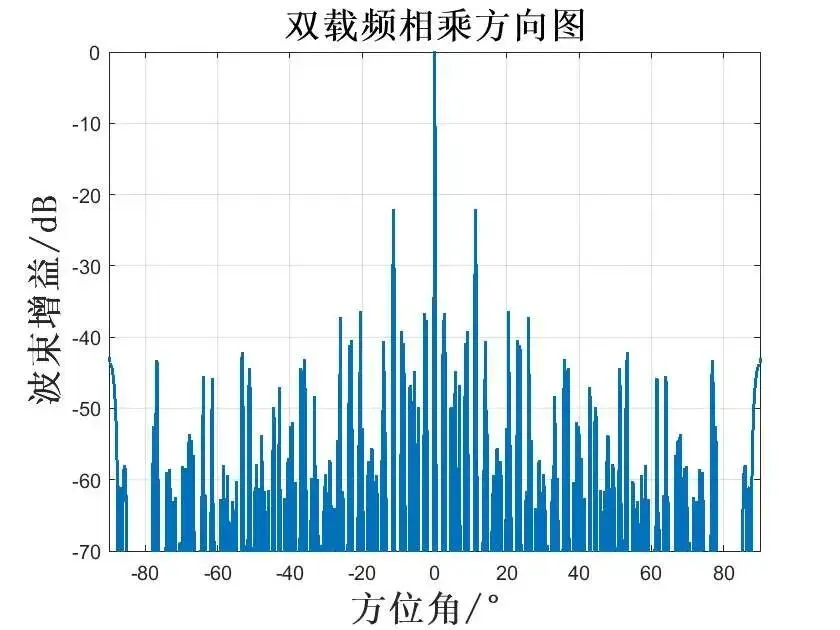
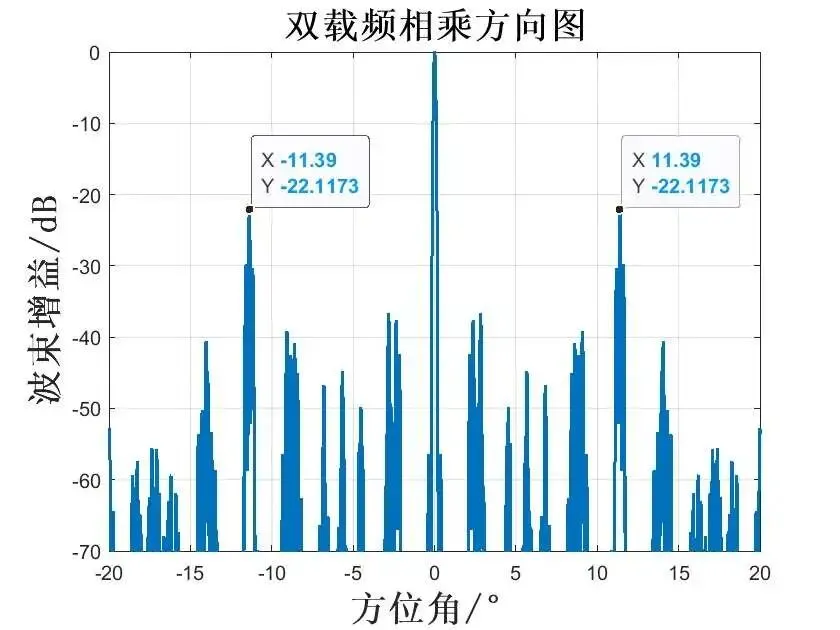
其实博主感觉从 和  角度出发其实也是合理的，这样也可以得到频率差阈值的范围。我们知道其实本质上是为了防止栅瓣重合，那么通过上面分析可知：

如果出现栅瓣重合，也即：

为了保证  最小，只能取到最大公约数的下一个值，也即：

那么可知：

这意味着安全频率差  跟阵列稀疏度  成反比！栅瓣越密，留给你调整频率的空间（安全间隙）就越小。

IV.PERFORMANCE ANALYSIS 算法性能分析

为进一步讨论该算法对栅瓣抑制的性能,给出以下公式推导证明。均匀稀疏分布的1维分布式MIMO阵列两组不同载频方向图相乘后得到的方向图  可表示为：

其中：

令 ，，，那么  可以表示为：

两组不同载频对应的阵列方向图相乘后的最大旁瓣出现位置  在两个方向图的第一个栅瓣之间，也即  对应的  处在  区间：

证明：首先，令：，，这两个点分别是  和  的栅瓣，也即最大值点，那么这两个点的导数都为零：

在区间左边：曲线正在上升（还没到顶）。说明最高点肯定在右边。

在区间右边：曲线正在下降（已经过了顶）。说明最高点肯定在左边。

结论：如果一个连续光滑的函数，在左头往上走，在右头往下走，那么它的最高点（极值点）一定在这个区间内部！

同时这里也有一个限制条件，单调性成立的前提，是频率差  足够小，使得两个栅瓣的错开距离，远小于它们自身的主瓣宽度。在这个前提下，区间  位于两座山的山顶平滑区域，所以可以使用单调性分析。证明了最大值必然在两峰之间。

在上面我们分析了栅瓣不重合的条件，对频率差进行了限制，下面所有的讨论均是在这个条件下进行的。同时为了评价栅瓣抑制算法的性能，以峰值旁瓣比（Peak SideLobe Ratio, PSLR）作为评价指标去衡量对栅瓣的抑制效果，峰值旁瓣比越小表示栅瓣抑制效果越好。

那么求解  最大旁瓣幅度首先应求解最大旁瓣对应的角度，也即可以写成如下的等价式：

通过上面可知， 在区间  区间内单调递增， 在区间  区间内单调递减。所以求解上式的最大值，可以等效为下式的问题：

当然这是有条件的，需要证明  关于  对称和  随  变化形状平移不变性。

证明（1）：

在这里我可以把上面的区间最一点扩展，我们知道原来的区间是：

又知道： 关于  对称，那么区间可以拓展到：

证明（2）：

又因为：

所以：

所以，在  范围内 ，“在这个小范围内，蓝色的鬼影 () 相比于红色的鬼影 ()，只是位置挪了一下，胖瘦根本没变！”

我觉得Gemini这里的解释很好，他是这样说的：

事实：  是由  产生的。因为频率变了 ()，理论上波束不仅会位移，还会变窄（也就是波形会发生“挤压”变形）。虽然理论上会变窄，但在那个极小的区间里，“变窄”的效应微乎其微，可以忽略不计。我们可以把  简单粗暴地看作是  平移后的结果。即：。

所以这句话是在说： 的形状在经历  的变化后，保持了“平移不变性”（Shape Invariance）。

翻译成公式就是， 在  范围内和  在  区间上长得一模一样。

在栅瓣附近的这个小范围内，我们可以认为  和  的波形形状完全一致（全等），唯一的区别就是  向左平移了一段距离  。

首先，为什么要把对  进行左移？我们知道， 的同级别的栅瓣都在  的左边，把  的一个栅瓣移动到  的第一个栅瓣位置，去看看  和  长得像不像，也即移动的位置是：。

同时为什么上面的等式是成立的？

这个因为：，或者更严谨的说，它还要除以光速，那就更是接近于零。

通过上面的所有分析，我们可知，当变量  取区间的中点时候，满足：

也即： 时， 在区间  区间取到最大值。

也即：

由此可以得到频率差与峰值旁瓣比（PSLR）的表达式：

上面这个其实很有趣，为了论证为什么在区间的中点 ，我们从最简单的例子出发，首先假设：

 在区间的右端点取到最大值并且在区间内单调递增， 在区间的左端点取到最大值在区间内单调递减，同时为了满足上述的对称性，我们可以得到下面的仿真图：

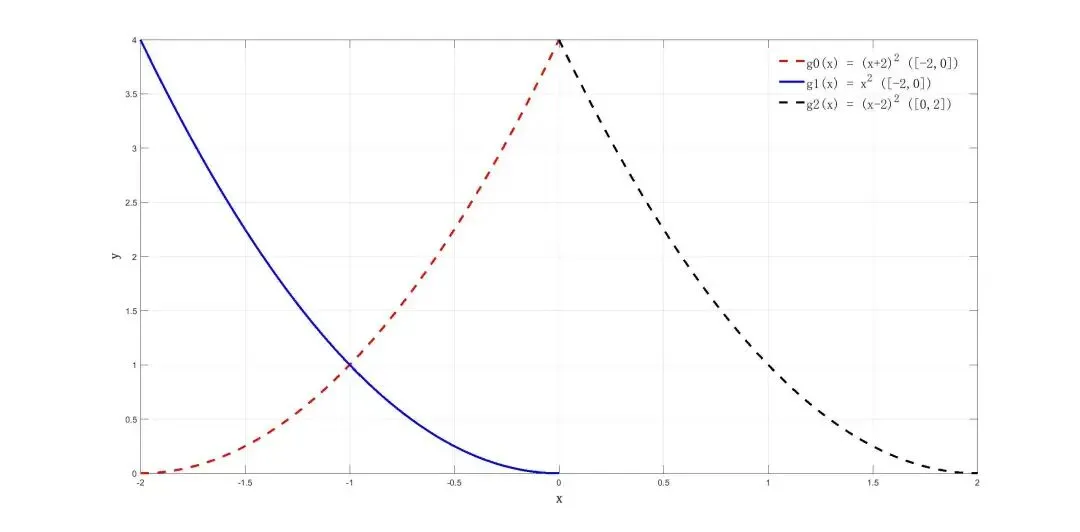
上面的图很好的解释了为什么当变量  取区间的中点时候，满足：

红色的线和黑色的关于  对称，然后蓝色的线平移后跟黑色的线相同，符合上面的对称性和平移不变性。

当频率差增大，整个  所属的区间也会增大。频率差  越大，蓝鬼影平移的距离  就越大。两个形状一样的山峰，中心距离越远，它们“撞车”的位置就越低。也即：在上面的限定的频率差范围内，PSLR随信号频率差增大而减小。

V.SIMULATION VERIFICAION 仿真验证

为了验证论文所介绍的栅瓣抑制算法原理的正确性以及栅瓣抑制性能。文章设计了由10个发射天线和10个接收天线组成的均匀稀疏分布的1维分布式MIMO阵列仿真实验，具体参数如表所示。

(1) 不同频率差下方向图相乘后方向图

在频率差系数为 0.013时，波束指向为  时，仿真如图所示:

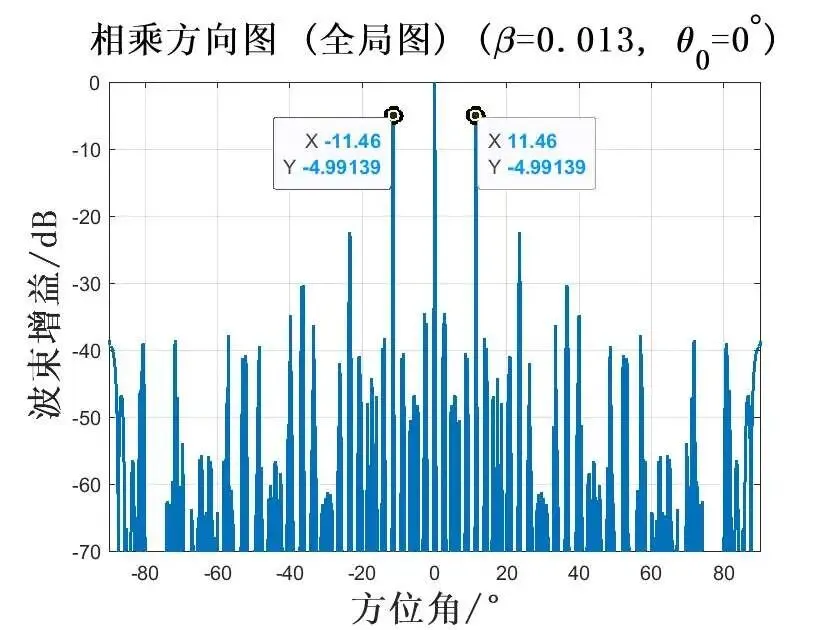
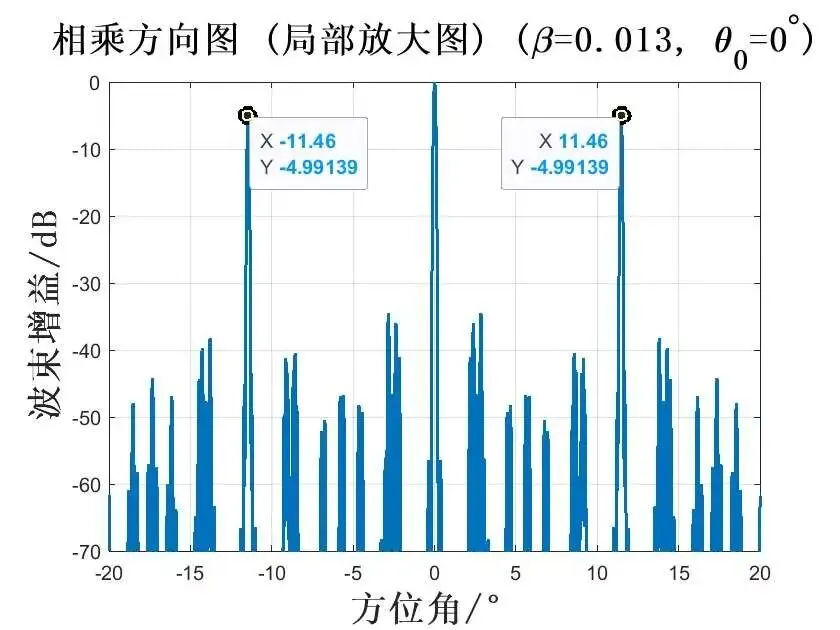
在频率差系数为 0.026时，波束指向为  时，仿真如图所示:

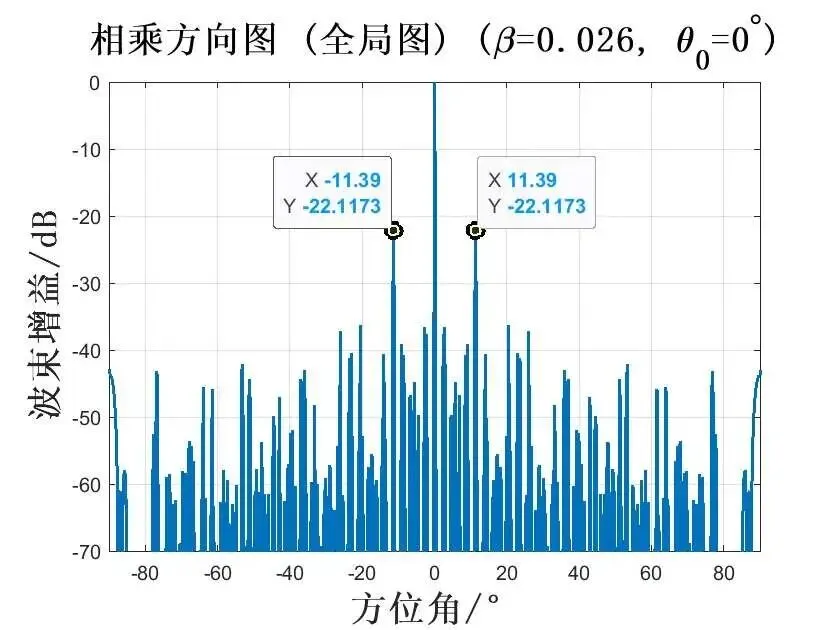
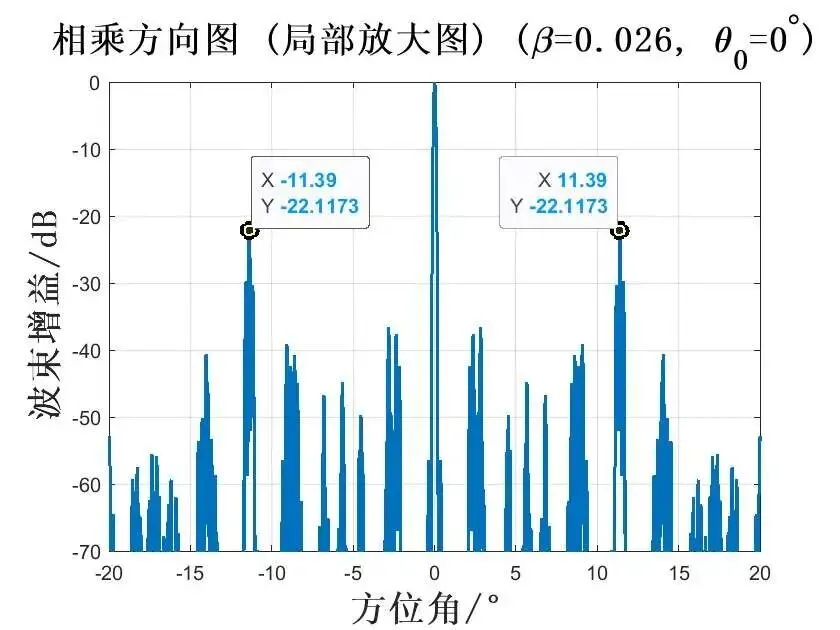
在频率差系数为 0.013时，波束指向为  时，仿真如图所示:

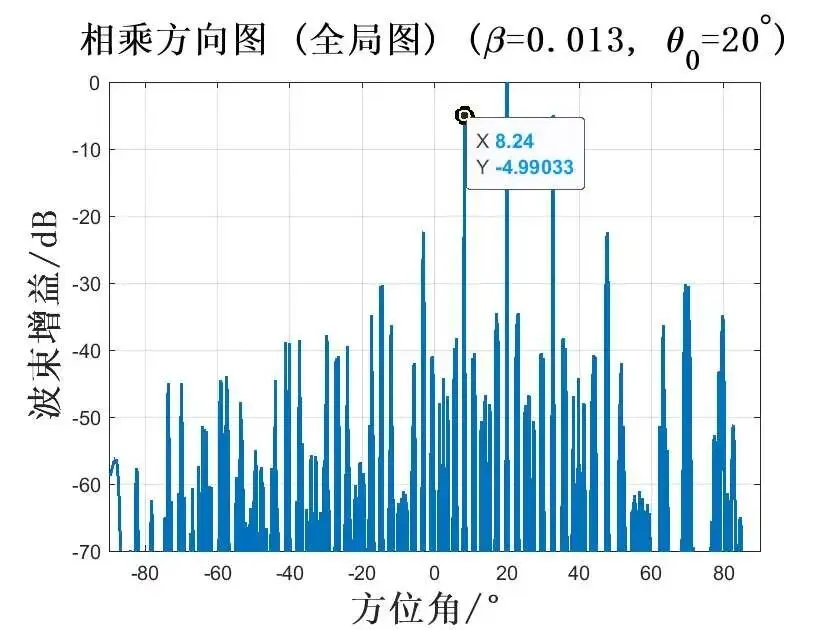
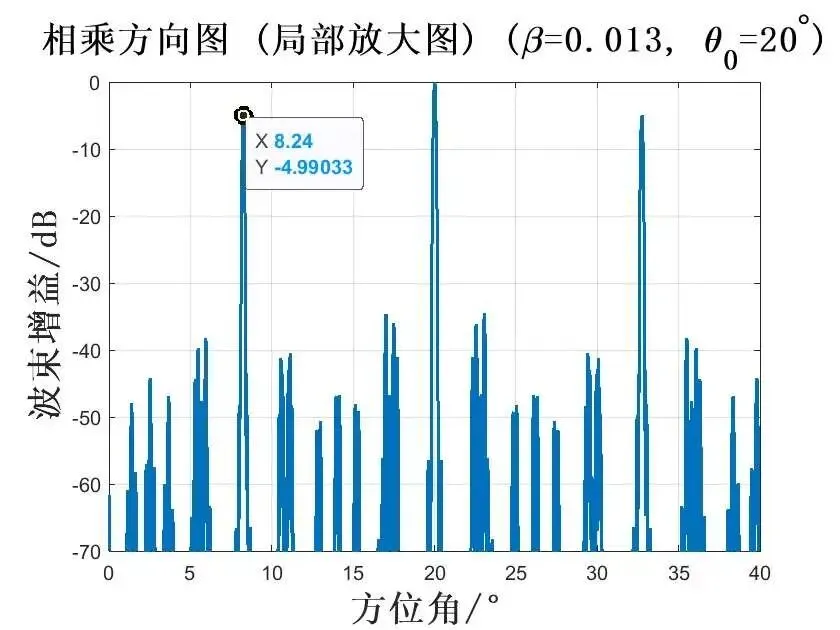
在频率差系数为 0.026时，波束指向为  时，仿真如图所示:

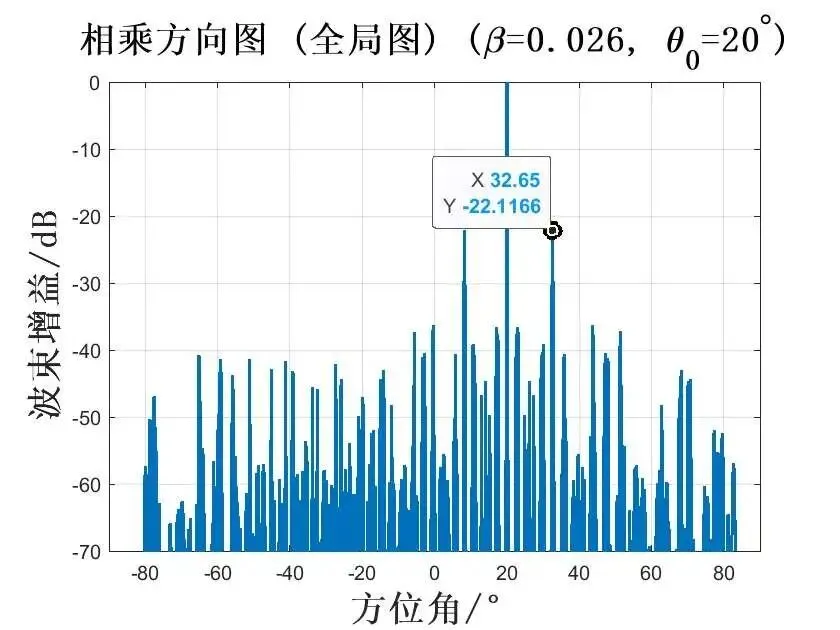
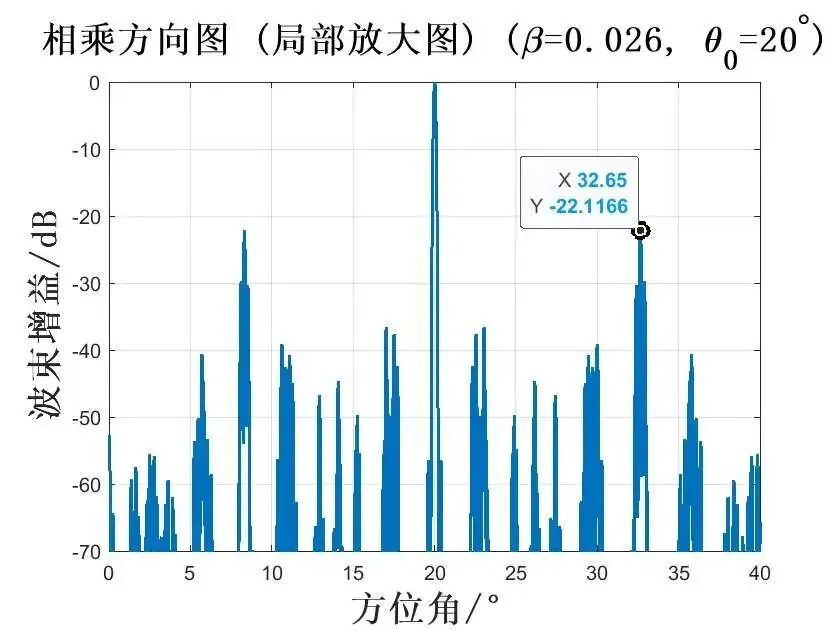
由此上面仿真图可知,天线波束进行扫描并不会影响算法的栅瓣抑制性能，同时基于不同载频方向图相乘的栅瓣抑制算法可以有效抑制栅瓣,而且栅瓣的抑制性能与频率差有关。

在这里需要说明的是，博主仿真得到的PSLR和原论文里的不同，同时改变波束指向PSLR的值也发生了一点变化，这是由于我的角度间隔比较大，把角度间隔缩小就是一样的，这仅仅是和精度有关。

(2) 栅瓣抑制性能与频率差的关系

由上面分析可知,该算法栅瓣抑制的性能与两组载频的频率差有关,在一定范围内频率差越大算法的栅瓣抑制性能越好。为验证本文所推导的该算法栅瓣抑制后峰值旁瓣比与频率差关系表达式的正确性,不失一般性地在表1所示仿真条件基础上设计了天线最大值指向为  时多组不同频率差的仿真实验。

两组不同载频对应的方向图相乘后得到方向图峰值旁瓣对应角度与频率差的关系曲线(近似值与理论值),如图所示。

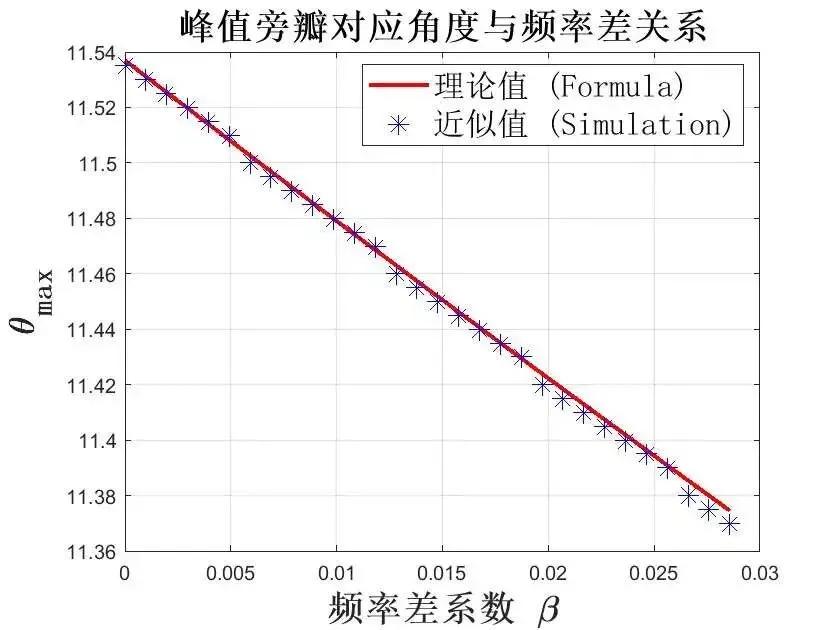
两组不同载频对应的阵列方向图相乘得到方向图的峰值旁瓣比与两组信号频率差的关系曲线(理论值),如图所示。

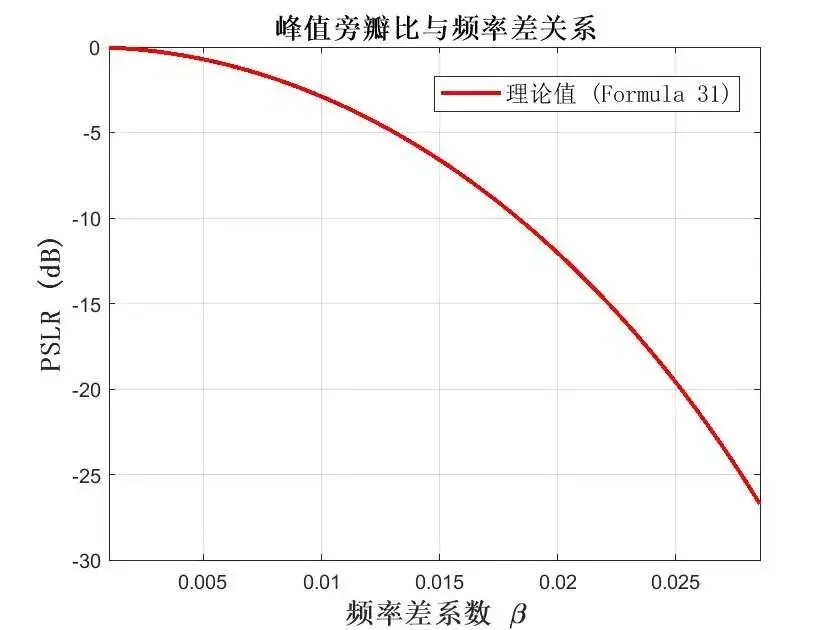
由上图可知,不同频率差下得到的近似峰值旁瓣比以及对应角度与理论峰值旁瓣比以及对应角度相吻合,由此验证该算法栅瓣抑制性能近似表达式的正确性。同时可知,在一定频率差范围内峰值旁瓣比随频率差值增大而减小。因此,频率差越大算法栅瓣抑制性能越强。

VI.CONCLUSION 总结

为了抑制稀疏阵列因天线稀疏分布而产生的大量栅瓣,本文提出一种利用双载频方向图相乘的栅瓣抑制算法。该算法利用不同载频阵列方向图主瓣与栅瓣相对位置关系存在差异的特性实现对栅瓣的有效抑制。在最优频率差下,该算法对稀疏阵列栅瓣有25dB的抑制效果,且存在无需进行大规模搜索的优势。文中推导得到的栅瓣抑制后峰值旁瓣比与频率差的关系表达式可以为雷达系统设计过程中快速选择最优频率差提供理论依据。

VII.REFERENCE 参考文献

1.王旭, 黄冬平, 魏国华, 等. 利用双载频方向图相乘的稀疏均匀阵栅瓣抑制方法[J]. 电子与信息学报, 2023, 45(2): 534-541.