跟老马一起“升级打怪”学编程！

• 涉及考试：计算机学会编程能力等级认证（GESP）
• 活动内容：提供不同等级的真题供小朋友们选择练习
• 备考建议：根据自己备考的等级选择相应题目
• 附加价值：可作为白名单比赛的备考训练
• 本月打卡：本月打卡题目

Day11：Openjudge1.4.16_三角形判断

【提交】

http://noi.openjudge.cn/ch0104/16/

【描述】

给定三个正整数，分别表示三条线段的长度，判断这三条线段能否构成一个三角形。

【输入】

给定三个正整数，分别表示三条线段的长度，判断这三条线段能否构成一个三角形。

【输出】

如果能构成三角形，则输出“yes” ，否则输出“no”。

【样例输入】

3 4 5

【样例输出】

yes

【参考程序】

C语言版本

/** 16:三角形判断* http://noi.openjudge.cn/ch0104/16/*/# include<cstdio>intmain(){int a, b, c;scanf("%d%d%d", &a, &b, &c);if (a + b > c && a + c > b && b + c > a)    {printf("yes");    }else    {printf("no");    }return 0;}

C++版本

/** 16:三角形判断* http://noi.openjudge.cn/ch0104/16/*/#include<iostream>#include<iomanip>using namespace std;intmain(){int a, b, c;cin >> a >> b >> c;if (a + b > c && a + c > b && b + c > a)    {cout << "yes";    }else    {cout << "no";    }return 0;}

Day11：Openjudge1.5.08_多边形内角和

【提交】

http://noi.openjudge.cn/ch0105/08/

【描述】

在欧几里德几何中， 边形的内角和是 。已知其中  个内角的度数，就能计算出剩下的一个未知内角的度数。请编写一个程序，来解决这个问题。

【输入】

第1行只有一个整数 ，第2行有  个正整数，是每个已知内角的度数。相邻两个整数之间用单个空格隔开。

数据保证给定多边形合法。

【输出】

一个正整数，为未知内角的度数。

【样例输入】

345 60

【样例输出】

75

【参考程序】

C语言版本

/** 08:多边形内角和* http://noi.openjudge.cn/ch0105/08/*/# include<cstdio>intmain(){int n, x;scanf("%d", &n);int sum = (n - 2) * 180;for (int i = 0;i < n - 1;i++)    {scanf("%d", &n);        sum -= x;    }printf("%d", sum);return 0;}

C++版本

/** 08:多边形内角和* http://noi.openjudge.cn/ch0105/08/*/# include<iostream>using namespace std;intmain(){int n,x;cin >> n;int sum = (n - 2) * 180;for (int i = 0;i < n - 1;i++)    {cin >> x;        sum -= x;    }cout << sum;return 0;}

Day11：Openjudge1.7.01_统计数字字符个数

【提交】

http://noi.openjudge.cn/ch0107/01/

【描述】

输入一行字符，统计出其中数字字符的个数。

【输入】

一行字符串，总长度不超过255。

【输出】

输出为1行，输出字符串里面数字字符的个数。

【样例输入】

Peking University is set up at 1898.

【样例输出】

4

【参考程序】

C++版本

/** 01:统计数字字符个数* http://noi.openjudge.cn/ch0107/01/*/#include<iostream>#include<string>using namespace std;intmain(){string str;    getline(cin, str, '\n');int count = 0;for (int i = 0; i < str.size(); i++)    {if (str[i] >= '0' && str[i] <= '9')        {            count += 1;        }    }cout << count;return 0;}

Day11：Openjudge1.8.04_错误探测

【提交】

http://noi.openjudge.cn/ch0108/04/

【描述】

给定由0和1组成的矩阵，如果矩阵的每一行和每一列的1的数量都是偶数，则认为符合条件。

你的任务就是检测矩阵是否符合条件，或者在仅改变一个矩阵元素的情况下能否符合条件。

"改变矩阵元素"的操作定义为0变成1或者1变成0。

【输入】

输入行，第1行为矩阵的大小，以下行为矩阵的每一行的元素，元素之间以一个空格分开。

【输出】

如果矩阵符合条件，则输出OK；

如果矩阵仅改变一个矩阵元素就能符合条件，则输出需要改变的元素所在的行号和列号，以一个空格分开。

如果不符合以上两条，输出Corrupt。

【样例输入】

样例输入141 0 1 00 0 0 01 1 1 10 1 0 1样例输入241 0 1 00 0 1 01 1 1 10 1 0 1样例输入341 0 1 00 1 1 01 1 1 10 1 0 1

【样例输出】

样例输出1OK样例输出22 3样例输出3Corrupt

【参考程序】

C++版本

/** 04:错误探测* http://noi.openjudge.cn/ch0108/04/*/# include<iostream>using namespace std;intmain(){int arr[105][105] = { 0 };int a[105] = { 0 };//存行累加，即1的个数int b[105] = { 0 };//存列累加，即1的个数int n;cin >> n;//读入数据for (int i = 1;i <= n;i++)    {for (int j = 1;j <= n;j++)        {cin >> arr[i][j];            a[i] += arr[i][j];//行累加        }    }//列累加for (int j = 1;j <= n;j++)    {for (int i = 1;i <= n;i++)        {            b[j] += arr[i][j];        }    }//计算行和列奇数的个数int cnt1 = 0, cnt2 = 0, r = 0, c = 0;for (int i = 1;i <= n;i++)    {if (a[i] % 2 != 0)        {            cnt1 += 1;            r = i;        }if (b[i] % 2 != 0)        {            cnt2 += 1;            c = i;        }    }//输出结果if (cnt1 == 0 && cnt2  == 0)    {//矩阵符合条件//没有奇数cout << "OK";    }else if (cnt1 == 1 && cnt2 == 1)    {//仅改变一个矩阵元素就能符合条件//只有一个奇数cout << r << " " << c;    }else    {cout << "Corrupt";    }return 0;}

Day11：GESP五级2024.06_黑白格

【提交】

https://www.luogu.com.cn/problem/P10719

【问题描述】

小杨有一个  行  列的网格图，其中每个格子要么是白色，要么是黑色。

小杨想知道至少包含  个黑色格子的最小子矩形包含了多少个格子。

【输入描述】

第一行包含三个正整数 ，含义如题面所示。

之后  行，每行⼀个长度为  的  串，代表网格图第  行格子的颜色，如果为 ，则对应格子为白色，否则为黑色。

【输出描述】

输出一个整数，代表至少包含  个黑色格子的最小子矩形包含格子的数量，如果不存在则输出 。

【样例输入1】

4 5 500000011110001100011

【样例输出1】

6

【样例解释】

对于样例 ，假设  代表第  行第  列，至少包含  个黑色格子的最小子矩形的四个顶点为 ，，，，共包含  个格子。

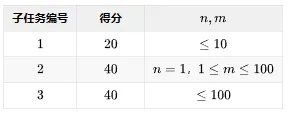
【数据范围】

对于全部数据，保证有 ，。

参考答案：

题目可以转化为元素和大于等于  的最小子矩阵中的元素个数。我们处理出矩阵的前缀和，然后暴力枚举子矩阵的左上和右下端点，若当前矩阵中元素和大于等于 ，则更新最小值。记得判不存在的情况。

/** GESP202406 五级 黑白格* https://www.luogu.com.cn/problem/P10719*/#include<iostream>#include<algorithm>using namespace std;const int N = 102;int a[N][N];int s[N][N];intmain(){int n, m, k;cin >> n >> m >> k;for (int i = 1; i <= n; i++)     {for (int j = 1; j <= m; j++)         {char c;cin >> c;            a[i][j] = c - '0';// 矩阵的前缀和            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];        }    }int mn = 0x0fffffff;for (int i1 = 1; i1 <= n; i1++)    {for (int j1 = 1; j1 <= m; j1++)        {for (int i2 = i1; i2 <= n; i2++)            {for (int j2 = j1; j2 <= m; j2++)                {// 从s[i1][j1] 到 s[i2][j2] 的子矩阵的和 if (s[i2][j2] - s[i1 - 1][j2] - s[i2][j1 - 1] + s[i1 - 1][j1 - 1] >= k)                    {                        mn = min(mn, (i2 - i1 + 1) * (j2 - j1 + 1));                    }                }            }        }    }if (mn != 0x0fffffff)    {cout << mn;    }else    {cout << 0;    }return 0;}

Day11：GESP六级2025.09_货物运输

【提交】

https://www.luogu.com.cn/problem/P14076

【问题描述】

A 国有  座城市，依次以  编号，其中  号城市为首都。这  座城市由  条双向道路连接，第  条道路（）连接编号为  的两座城市，道路长度为 。任意两座城市间均可通过双向道路到达。

现在 A 国需要从首都向各个城市运送货物。具体来说，满载货物的车队会从首都开出，经过一座城市时将对应的货物送出，因此车队需要经过所有城市。A 国希望你设计一条路线，在从首都出发经过所有城市的前提下，最小化经过的道路长度总和。注意一座城市可以经过多次，车队最后可以不返回首都。

【输入描述】

第一行，一个正整数 ，表示 A 国的城市数量。

接下来  行，每行三个正整数 ，表示一条双向道路连接编号为  的两座城市，道路长度为 。

【输出描述】

一行，一个整数，表示你设计的路线所经过的道路长度总和。

【样例输入1】

41 2 61 3 13 4 5

【样例输出1】

18

【样例输入2】

71 2 12 3 13 4 17 6 16 5 15 1 1

【样例输出2】

9

【说明/提示】

对于  的测试点，保证 。

对于另外  的测试点，保证仅与一条双向道路连接的城市恰有两座。

对于所有测试点，保证 ，，。

参考答案：

沿着树进行深度优先遍历，但不需要回溯到最后访问的节点。总路径长度等于所有边权之和的两倍减去从首都出发的最长路径长度。

算法思路：

• 构建树的邻接表表示
• 从首都（节点1）开始进行DFS，计算每个节点到首都的距离
• 找到距离首都最远的节点（最长路径）
• 总路径长度 = 2 × 所有边权之和 - 最长路径长度

/** [GESP202509 六级] 货物运输* https://www.luogu.com.cn/problem/P14076*/# include<iostream># include<vector>using namespace std;vector<vector<pair<int, long long>>> graph; // 邻接表vector<long long> dist; // 存储每个节点到首都的距离long long total_length = 0; // 所有边的总长度long long max_dist = 0; // 距离首都最远的距离voiddfs(int node, int parent, longlong current_dist){    dist[node] = current_dist;    max_dist = max(max_dist, current_dist);for (pair<int,long long> neighbor : graph[node])     {int next_node = neighbor.first;long long edge_length = neighbor.second;if (next_node != parent)         {            dfs(next_node, node, current_dist + edge_length);        }    }}intmain(){int n;cin >> n;    graph.resize(n + 1);    dist.resize(n + 1, 0);// 读取n-1条边for (int i = 0; i < n - 1; i++)     {int u, v;long long l;cin >> u >> v >> l;        graph[u].push_back({ v, l });        graph[v].push_back({ u, l });        total_length += l;    }// 从首都（节点1）开始DFS    dfs(1, -1, 0);// 计算最小总路径长度long long min_total_path = 2 * total_length - max_dist;cout << min_total_path << endl;return0;}

青少年编程竞赛交流