数学上将一维数组称为向量,将二维数组称为矩阵,三维数组称为张量。
标量(Scalar):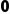 维,就是一个简单的数字(如
维,就是一个简单的数字(如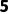 )。
)。
提供(向量):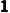 维,一行或一列数字。
维,一行或一列数字。
矩阵(Matrix):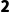 维,像Excel表格一样有行有列。
维,像Excel表格一样有行有列。
张量 (Tensor):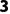 维及以上。
维及以上。
简单来说,广播就是 NumPy 的“自动伸缩术”。当两个队列形状不同但又要进行轰炸(加减乘除)时,NumPy 会在后台自动增加放大的队列,让它们对齐。
第一步:核心规则(准入门槛)
不是任何两个形状的阵列均匀广播。NumPy 遵循一个“从后到前”的匹配准则。
当你比较多个数据库时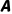 和
和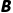 的形状时,从各个形状的最后(最右边)一个维度开始垂直,如果这两个维度满足以下任一条件,则该维度“兼容”:
的形状时,从各个形状的最后(最右边)一个维度开始垂直,如果这两个维度满足以下任一条件,则该维度“兼容”:
1.数字充足。
2.其中一个是1 (关键:1就是那个可以被“拉伸”的维度)。
如果备份在所有维度上都兼容,就能获得两个广播成功。
第二步:动态图解(脑补过程)
想象一下这个过程:
·如果维度数量不同:维度数量会在其左边补上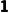 。
。
o例如: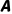 是
是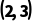 是
是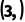 。
。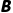 会先变成
会先变成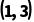 。
。
·如果长度为 1:该维度会沿另一个阵列在该维度上的长度进行“自我复制”。
o接上例:的形状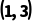 在第一个轴上是
在第一个轴上是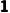 ,它会垂直复制一份,变成
,它会垂直复制一份,变成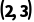 。
。
第三步:三个典型案例拆解
案例A:完美的“拉伸”(矩阵+搬运)
·形状: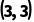
·B 形状: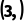
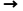 补1变成
补1变成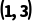
·匹配过程:
o维度:都是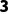 ,好的。
,好的。
o倒数第二维度:一个是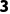 ,一个是
,一个是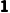 ,好的(
,好的(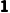 可以拉伸到
可以拉伸到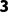 )。
)。
·结果: 广播成功,结果形状是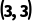 。
。
案例B:两个方向均在“拉伸”(列承载+行承载)
这是最神奇的一种,双方都在互相迁徙。
·形状: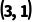 (这是一个3行1列的列管理)
(这是一个3行1列的列管理)
·B 形状: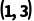 (这是一个 1 行 3 列的行服务)
(这是一个 1 行 3 列的行服务)
·匹配过程:
o维度:一个是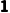 ,一个是
,一个是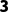 ,好的。
,好的。
o倒数第二维度:一个是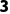 ,一个是
,一个是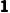 ,好的。
,好的。
·结果: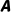 往左拉伸,
往左拉伸,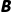 往纵向牵引,最终生成一个
往纵向牵引,最终生成一个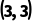 的矩阵!
的矩阵!
案例C:报错的陷阱(无法匹配)
·形状: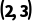
·B 形状: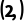
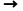 补1变成
补1变成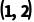
·匹配过程:
o维度:一个是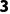 ,一个是
,一个是 。不充足,且没有一个是 1 。
。不充足,且没有一个是 1 。
·结果:报错 (ValueError)。这就是我上次提到的,必须从右往左扫描的原因。
总结
广播的核心就是:在设备或长度为1的轴上进行“疯狂复制”,直到形状完全一样。