【Python学习】Sklearn入门实战-数字识别与房价预测【附源码】
- 2026-02-05 09:14:20
本文包含大量可运行代码,建议在电脑上阅读并实践。
什么是机器学习
机器学习是人工智能领域的一项关键技术,它让计算机系统通过从大量数据中学习和积累经验,不断提升自身性能。简单来说,机器学习就是让计算机具备从数据中自动发现规律,并利用这些规律对新数据进行预测或决策的能力。
比如,当我们在手机上用人脸解锁功能时,背后就是一个机器学习模型——它学习了成千上万张人脸图片的特征,从而能够准确识别出你的面孔。
机器学习的四大类型
根据学习任务模式(训练数据是否有标签),机器学习可分为以下四大类:
监督学习(有标签):数据带 “标准答案”,比如给手写数字图片标上 “0-9”,让计算机学 “什么样的像素对应什么数字”,适合分类(判断邮件是否为垃圾邮件、识别图片中的动物种类)、预测任务(预测房价、股票价格等连续数值)。
无监督学习(无标签):数据没标准答案,让计算机自己找规律,比如把用户购物记录分成不同群体,适合聚类、找趋势;
半监督学习(有部分标签):少量数据有答案,大量数据没答案,比如只有 100 张手写数字标了标签,剩下 900 张没标,结合两者学习;
强化学习(有评级标签):智能体通过与环境互动,根据奖励调整行为,像 “闯关升级”,计算机做动作后得到 “奖励” 或 “惩罚”,慢慢学会最优策略,比如游戏 AI、自动驾驶。
对入门来说,监督学习最直观,我们后面的案例也聚焦这一类型。
机器学习神器——Sklearn
sklearn(又写作scikit-learn)是一款开源的 Python 机器学习库,它基于 NumPy、SciPy 和 Matplotlib 等 Python 库来实现高效的算法应用,并且涵盖几乎所有主流机器学习算法,无需我们从零造轮子。同时它自带数据集,不用手动下载数据,直接导入手写数字、鸢尾花、房价等数据集,就能快速上手机器学习实战。
一、基于sklearn的机器学习的一般流程为
数据获取→ 数据预处理→模型训练→ 模型评估→模型应用
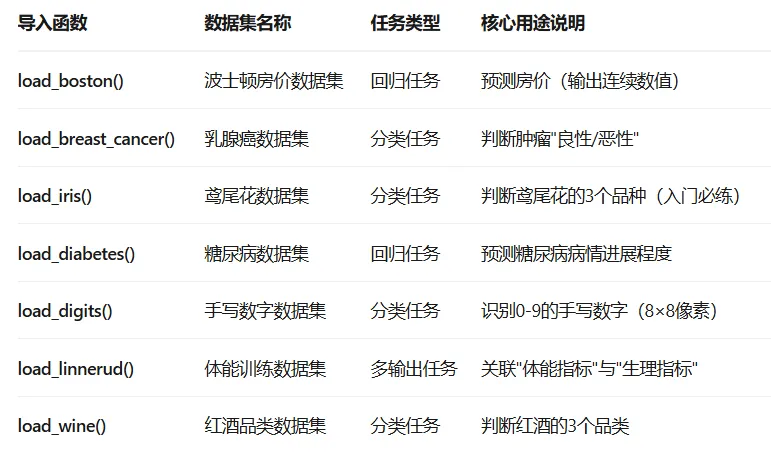
二、sklearn内置核心数据集
三、案例实战
下面的案例循序渐进,所有代码都带详细注释,复制到 PyCharm 或 IDLE 就能运行。
案例1:计算机看到的世界
计算机看到的世界和我们完全不同。对我们来说,数字"0"是一个圆形的图像;但对计算机来说,它看到的是一堆数字组成的矩阵。
import matplotlib.pyplot as pltfrom sklearn import datasets# 解决中文显示问题plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示问题plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 加载手写数字数据集(Sklearn内置)#digits 里包含所有图片(images)和对应的数字标签(target)digits = datasets.load_digits()# 获取数据集中的第一个图像(第1个样本)及其标签digital = digits.images[0] # 第一个图像的像素矩阵label = digits.target[0] # 第一个图像对应的数字标签# 打印图像的像素矩阵print("手写数字的像素矩阵:")print(digital)# 打印对应的标签(实际数字)print("\n手写数字为:", label)# 绘制图像时,增加标题显示数字标签plt.title(f"手写数字:{label}") # 新增这一行plt.axis('off') # 关闭坐标轴显示# 以灰度反转模式显示图像#imshow:把像素矩阵转换成图像显示;#cmap='gray_r':用“灰度反转”模式显示(数字的笔画是黑色、背景是白色,更符合手写数字的视觉习惯)。plt.imshow(digital, cmap=plt.get_cmap('gray_r'))plt.show() # 显示图像
这段代码的主要功能是:从 scikit-learn 的 datasets 模块中加载手写数字数据集,获取其中索引为 0 的手写数字图像及其对应的标签,然后在控制台打印该图像的矩阵形式和标签,并通过 matplotlib 库将该手写数字以灰度图像的形式显示出来,方便直观地观察手写数字数据集的内容。
运行后,你会看到控制台输出一个 8x8 的像素矩阵(因为该数据集的每个手写数字图像都是 8x8 像素),然后显示对应的数字标签,最后弹出一个窗口显示该手写数字的图像。
运行结果:
控制台会显示一个8×8的数字矩阵,这个矩阵就是计算机眼中的"数字0",每个数字代表一个像素点的明暗程度(0是最暗的黑色,15是最亮的白色)。
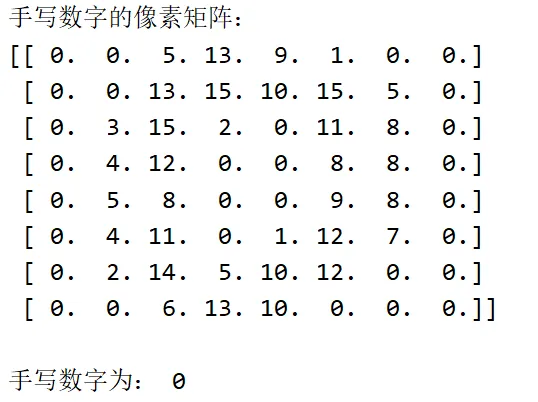
图1 计算机看到的世界
弹窗会显示对应的灰度图像,让我们能够直观看到。

图2 人看到的世界
案例2:了解手写数字数据集
在开始建模前,我们需要先了解数据集的情况,学会提取任意样本。
import matplotlib.pyplot as pltfrom sklearn import datasetsimport numpy as np# 解决中文显示问题plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False# 加载数据集digits = datasets.load_digits()# 1. 查看数据集基本信息print(f"样本总数:{digits.images.shape[0]} 张") # 1797张手写数字print(f"每张图片尺寸:{digits.images.shape[1:]} 像素") # 8×8像素print(f"标签数量:{digits.target.shape[0]} 个") # 每个样本对应一个标签# 2. 统计0-9每个数字的样本数print("\n0-9数字的样本分布:")for i in range(10):count = np.sum(digits.target == i)print(f"数字{i}:{count} 张")#前 20 个索引对应的数字:print("前20个索引对应的数字:")for i in range(20):print(f"索引{i} → 数字{digits.target[i]}")# 3. 显示任意一个样本(修改index可查看不同样本)index = 9 # 可改为0-1796之间的任意整数digital = digits.images[index]label = digits.target[index]print(f"\n第{index}个样本的像素矩阵:")print(digital)print(f"对应的数字:{label}")# 可视化该样本plt.figure(figsize=(4, 4))plt.axis('off')plt.imshow(digital, cmap='gray_r')plt.title(f"第{index}个样本(数字:{label})")plt.show()
运行结果:
 |  | 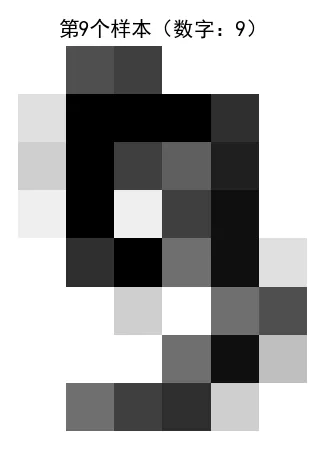 |
案例3:用KNN算法实现数字识别
现在让我们真正开始机器学习!我们将使用K最近邻(KNN)算法,它的思想非常直观:"物以类聚,人以群分"。
核心逻辑是 “找最像的 5 个样本投票”。
from sklearn import datasetsfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn.model_selection import train_test_splitimport matplotlib.pyplot as plt# 解决中文乱码问题plt.rcParams['font.sans-serif'] = ['SimHei'] # 支持中文显示plt.rcParams['axes.unicode_minus'] = False # 解决负号显示异常问题# 1. 加载手写数字数据集digits = datasets.load_digits()print("数据集基本信息:")print(f"样本总数:{digits.images.shape[0]} 张")print(f"每张图片尺寸:{digits.images.shape[1:]} 像素")print(f"数字类别:0-9(共{len(digits.target_names)}类)\n")# 2. 数据预处理:将8×8的二维像素矩阵转为一维数组(模型要求输入为一维特征)# 原数据:digits.images 是 (1797, 8, 8) 的三维数组(1797张图,每张8×8)# 转换后:X 是 (1797, 64) 的二维数组(1797个样本,每个样本64个特征=8×8)X = digits.images.reshape((digits.images.shape[0], -1))# 标签:digits.target 是每个样本对应的真实数字(0-9)y = digits.target# 3. 拆分训练集和测试集(用70%数据训练模型,30%数据测试效果)# random_state=42 确保每次运行结果一致X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)print(f"训练集样本数:{X_train.shape[0]}")print(f"测试集样本数:{X_test.shape[0]}\n")# 4. 创建并训练KNN模型(n_neighbors=5:找最近的5个样本判断类别,可修改尝试)knn_model = KNeighborsClassifier(n_neighbors=5)# 用训练集数据训练模型(模型学习像素特征与数字的对应关系)knn_model.fit(X_train, y_train)# 5. 模型预测与效果评估# 用测试集预测数字y_pred = knn_model.predict(X_test)# 计算准确率(正确预测的样本数/总测试样本数)accuracy = knn_model.score(X_test, y_test)print(f"KNN模型数字识别准确率:{accuracy:.2f}(即{accuracy*100:.1f}%的数字能被正确识别)\n")# 6. 可视化结果:展示前10个测试样本的真实值vs预测值plt.figure(figsize=(12, 4)) # 设置图片大小for i in range(10):# 子图布局:1行10列,第i+1个位置plt.subplot(1, 10, i+1)# 还原图像维度:将64维一维数组转回8×8二维矩阵plt.imshow(X_test[i].reshape(8, 8), cmap=plt.cm.gray_r) # 灰度反转显示(笔画黑、背景白)# 标题显示:真实数字 vs 预测数字plt.title(f"真实:{y_test[i]}\n预测:{y_pred[i]}")plt.axis('off') # 关闭坐标轴,更清晰plt.tight_layout() # 自动调整子图间距plt.show() # 显示图片
 |  |
案例4:用线性回归预测房价
除了分类问题,机器学习还能解决回归问题。让我们看一个简单的房价预测例子(输出连续数值),核心逻辑是 “找特征和房价的线性规律”。
代码段1:训练模型 + 预测 2025 年房价,控制台输出
# 导入所需库from sklearn.linear_model import LinearRegressionimport numpy as np# 2015-2024年年份+带波动房价(单位:元,无重复,整体上升)x = np.array([2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024])y = np.array([285000, 308000, 312000, 330000, 345000, 372000, 380000, 405000, 410000, 432000])# 将样本数据reshape为二维数组(满足sklearn模型输入要求,不可省略)x = x.reshape((-1, 1))# 创建线性回归模型实例model = LinearRegression()# 将模型拟合到样本数据上(训练模型,学习年份与房价的关联规律)model.fit(x, y)# 构造测试数据(预测2025年房价,全新未出现过的数据)x_test = np.array([2025]).reshape((-1, 1))# 使用训练好的模型进行预测y_predict = model.predict(x_test)# 输出预测结果(格式化输出,更易读)print("2025年房价预测值为:", f"{y_predict[0]:.2f} 元")
运行结果:2025年房价预测值为: 447200.00 元
代码段2:拟合效果,图表可视化输出
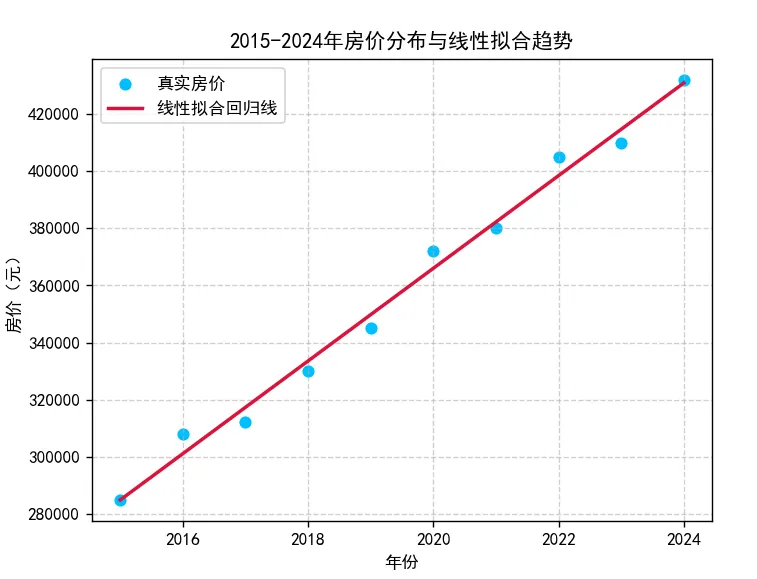
# 导入所需库import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression# 2015-2024年年份+带波动房价x = np.array([2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024])y = np.array([285000, 308000, 312000, 330000, 345000, 372000, 380000, 405000, 410000, 432000])# 创建线性回归模型实例model = LinearRegression()# 训练模型(内嵌reshape,省略中间变量,代码更简洁)model.fit(x.reshape(-1, 1), y)# 对训练数据进行拟合预测(用于绘制回归线)y_predict = model.predict(x.reshape(-1, 1))# 绘制可视化图表plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示乱码plt.rcParams['axes.unicode_minus'] = False # 解决负号显示异常plt.scatter(x, y, color='deepskyblue', label='真实房价') # 绘制真实房价散点图plt.plot(x, y_predict, color='crimson', linewidth=2, label='线性拟合回归线') # 绘制拟合回归线# 设置图表标签和标题plt.xlabel('年份')plt.ylabel('房价(元)')plt.title('2015-2024年房价分布与线性拟合趋势')plt.legend() # 显示图例plt.grid(linestyle='--', alpha=0.6) # 添加网格线,便于读数plt.show() # 显示图表
运行结果:弹出可视化图表,展示真实房价散点与线性拟合回归线。
代码3:可视化+2025年房价预测
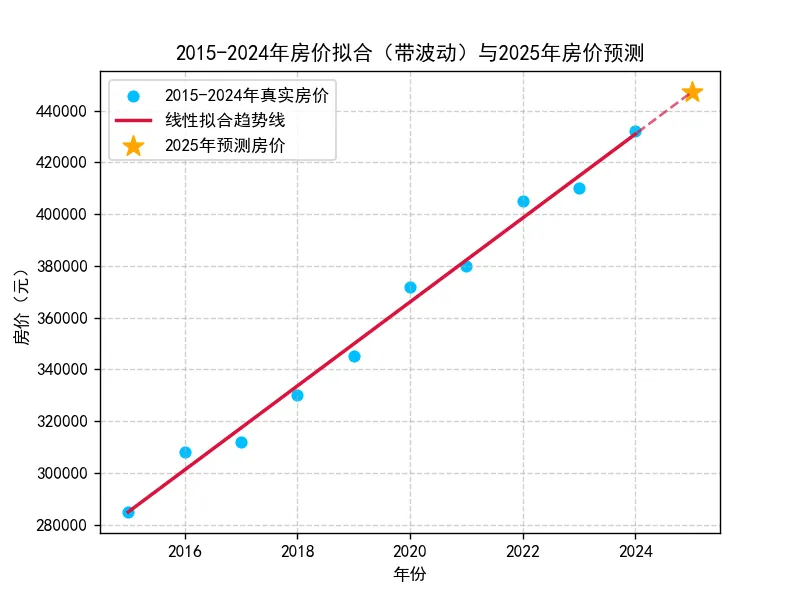
# 导入所需库import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression# 2015-2024年年份+带波动房价x = np.array([2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024])y = np.array([285000, 308000, 312000, 330000, 345000, 372000, 380000, 405000, 410000, 432000])# 创建线性回归模型实例model = LinearRegression()# 训练模型(内嵌reshape,满足sklearn输入要求,无需额外拆分步骤)model.fit(x.reshape(-1, 1), y)# 1. 对已有训练数据拟合预测(用于绘制回归线)y_fit = model.predict(x.reshape(-1, 1))# 2. 预测2025年房价(构造新测试数据+模型预测)x_2025 = np.array([2025]).reshape(-1, 1) # 新测试数据,需转为二维数组y_2025_predict = model.predict(x_2025) # 预测2025年房价# 绘制可视化图表(保留原有效果,新增预测值标注)plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决Windows中文乱码plt.rcParams['axes.unicode_minus'] = False # 解决负号显示异常# 原有:真实房价散点图plt.scatter(x, y, color='deepskyblue', label='2015-2024年真实房价')# 原有:线性拟合回归线plt.plot(x, y_fit, color='crimson', linewidth=2, label='线性拟合趋势线')# 新增:2025年预测房价标注(橙色*形,醒目易识别)plt.scatter(2025, y_2025_predict, color='orange', s=150, marker='*', label='2025年预测房价')# 可选优化:延长回归线到2025年,让趋势更连贯(非必须,更直观)x_extended = np.append(x, 2025) # 合并原有年份和2025年y_extended_fit = model.predict(x_extended.reshape(-1, 1)) # 对延长后的年份拟合plt.plot(x_extended, y_extended_fit, color='crimson', linestyle='--', alpha=0.7) # 虚线延长趋势线# 设置图表标签和标题plt.xlabel('年份')plt.ylabel('房价(元)')plt.title('2015-2024年房价拟合(带波动)与2025年房价预测')plt.legend() # 显示图例(区分真实值、拟合线、预测值)plt.grid(linestyle='--', alpha=0.6) # 网格线辅助读数plt.show() # 显示图表# 控制台输出2025年预测结果print(f"2025年房价预测值为:{y_2025_predict[0]:.2f} 元")
运行结果:2025 年房价预测值为:447200.00 元,同时弹出包含真实房价、拟合线和 2025 年预测值的可视化图表。
如果时间充裕,你也可以试试使用KNN实现鸢尾花分类器,SVM实现数字识别,熟能生巧。
机器学习入门必学3个库,可以参考前面这篇文章:
【Python学习】机器学习入门必学:NumPy、Pandas、Matplotlib三剑客【附源码】
如果这篇文章对你有帮助,请记得关注、点赞、在看、转发,谢谢
