Python | Skyborn | 涌现约束法
- 2026-01-11 14:22:59
Python | Skyborn | 涌现约束法
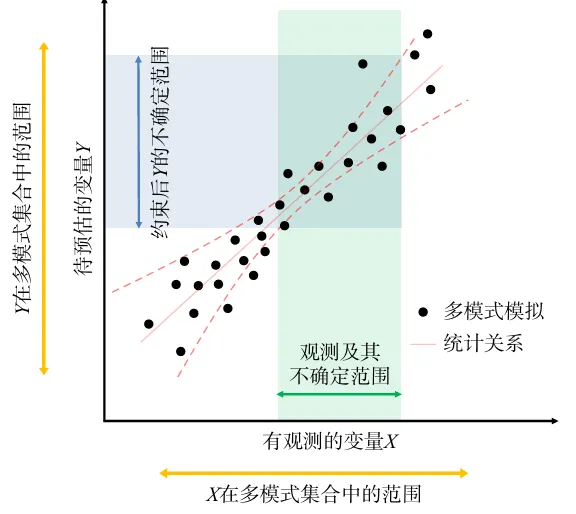
涌现约束法示意图 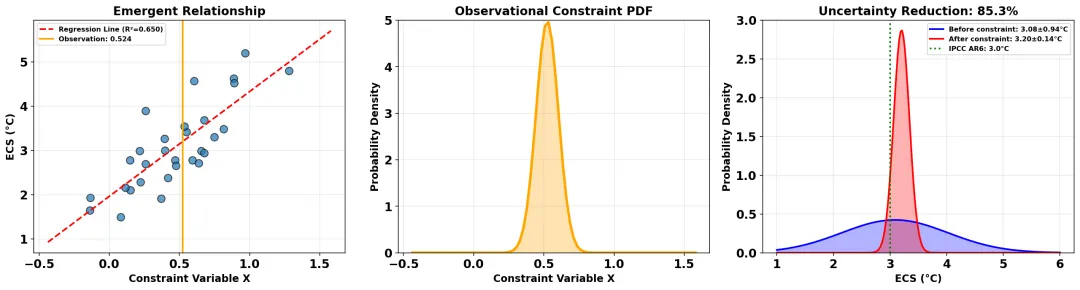

涌现约束法(Emergent Constraints)
用观测数据“校准”气候模型不确定性
在气候科学中,我们经常面对这样一道难题:不同气候模式(CMIP 家族)对未来变暖幅度给出截然不同的预测。如何在不更改模式物理的前提下,利用现有观测信息提升未来预测的可信度?
答案之一,就是——涌现约束法(Emergent Constraints)。
它的核心思想非常朴素:
先在多模式集合中找到“可观测变量 X”和“关心的未来量 Y(如 ECS)”之间的跨模式统计关系; 再用真实世界对 X 的观测值去约束 Y 的概率分布,从而降低预测不确定性。
典型应用:用云反馈相关的可观测量去约束平衡气候敏感度(ECS)。
核心原理:从跨模式关系到贝叶斯后验

设:
X = 约束变量(可观测,如云反馈指标) Y = 目标变量(未来或难以直接观测,如 ECS) 在模式集合上,X 与 Y 呈线性关系:Y = a·X + b + ε
步骤如下:
在模式集合内做回归,得到 a、b,以及预测残差不确定度 σ_pred; 根据观测获得 X 的观测概率密度函数 PDF_obs(X)(通常假设高斯:N(μ_obs, σ_obs)); 利用似然与观测先验对 Y 做积分,得到后验 PDF_post(Y): 直观理解:对每个可能的 X_obs,用回归关系映射到 Y,并按 PDF_obs(X) 加权求和; 从 PDF_post(Y) 中得到后验均值与标准差,实现对 Y 的不确定性收缩。
这正是 Skyborn 在 skyborn.calc.emergent_constraints 中实现的流程:
gaussian_pdf():高斯 PDF;emergent_constraint_prior():先验(由回归和预测误差给出);emergent_constraint_posterior():融合观测得到后验 PDF 与统计量。

为什么它有效?
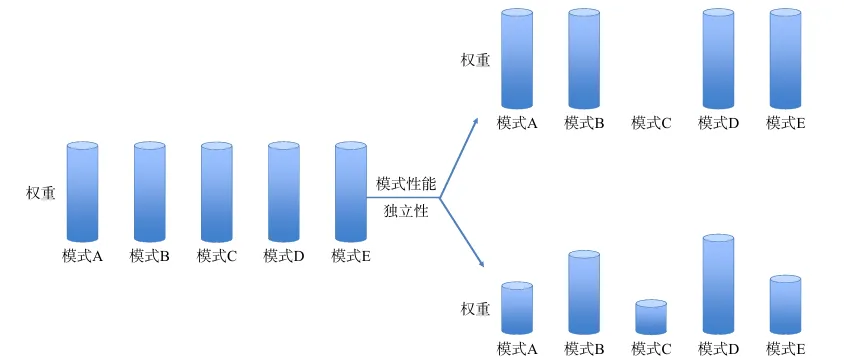
多模式集合中,若某一可观测过程(如低云反馈敏感度)与目标变量(ECS)存在稳健的跨模式关系,那么对该过程的观测就能“筛选”更可信的模式行为; 这不是简单“挑模型”,而是对概率分布进行贝叶斯更新:结果通常表现为标准差显著降低(常见 20–50%)。

方法适用与注意事项
相关性要求:跨模式关系应有足够统计显著性与物理依据(而非偶然相关); 观测不确定度:需要合理评估 X 的观测误差(σ_obs),避免过度自信; 外推风险:观测 X 若落在模式样本之外,需谨慎解读(可能存在外推误差); 物理一致性:优先选择受控、可解释、与目标物理过程紧密相连的约束变量。
实践指南:从基础到应用
安装与导入
# 安装 Skybornpip install skyborn# 或使用国内镜像加速pip install -i https://pypi.tuna.tsinghua.edu.cn/simple skyborn# 导入核心函数import numpy as npimport xarray as xrfrom skyborn.calc import ( gaussian_pdf, # 高斯概率密度函数 emergent_constraint_posterior, # 后验分布计算 emergent_constraint_prior, # 先验分布计算 pearson_correlation # 相关系数计算)基础应用:使用 Skyborn 函数
1. 计算高斯概率密度函数
import numpy as npfrom skyborn.calc import gaussian_pdf# 定义参数mu = 3.0# 均值sigma = 0.5# 标准差x = np.linspace(1.0, 5.0, 100) # 评估点# 计算 PDFpdf = gaussian_pdf(mu, sigma, x)2. 计算跨模式相关性
from skyborn.calc import pearson_correlation# 模拟数据:约束变量 X 与目标变量 Yconstraint_var = np.array([0.3, 0.5, 0.7, 0.9, 1.1]) # 例如:云反馈参数ecs_values = np.array([2.5, 3.0, 3.5, 4.0, 4.5]) # 平衡气候敏感度# 计算相关系数r = pearson_correlation(constraint_var, ecs_values)完整案例:ECS 涌现约束分析
以下是一个完整的涌现约束分析流程:
步骤 1:准备模式集合数据
import numpy as npimport xarray as xr# 模拟 30 个气候模式的数据np.random.seed(42)n_models = 30# 生成 ECS 值(基于 CMIP6 真实范围)ecs_values = np.random.normal(3.2, 0.9, n_models)ecs_values = np.clip(ecs_values, 1.5, 5.5)ecs_values[0:3] = [2.1, 4.8, 5.2] # 添加极端值# 生成约束变量(例如:热带低云反馈指标)# 与 ECS 有物理关联,但包含噪声constraint_strength = 0.7noise_level = np.sqrt(1 - constraint_strength**2)ecs_normalized = (ecs_values - ecs_values.mean()) / ecs_values.std()constraint_var = constraint_strength * ecs_normalized + noise_level * np.random.randn(n_models)constraint_var = constraint_var * 0.3 + 0.5# 缩放到合理物理范围步骤 2:建立涌现关系
from skyborn.calc import pearson_correlation# 计算跨模式相关性correlation = pearson_correlation(constraint_var, ecs_values)# 线性回归slope, intercept = np.polyfit(constraint_var, ecs_values, 1)步骤 3:引入观测约束
from skyborn.calc import gaussian_pdf# 观测数据(例如:卫星观测的云反馈参数)obs_mean = constraint_var.mean() + 0.05# 观测均值obs_std = 0.08# 观测不确定性# 设置计算网格constraint_grid = np.linspace(constraint_var.min() - 0.3, constraint_var.max() + 0.3, 80)ecs_grid = np.linspace(1.5, 5.5, 80)# 计算观测的概率密度函数obs_pdf = gaussian_pdf(obs_mean, obs_std, constraint_grid)步骤 4:计算约束后的 ECS 分布
# 方法 1:简化方法(基于线性回归)predicted_ecs = slope * constraint_var + interceptresiduals = ecs_values - predicted_ecsprediction_error = np.std(residuals)# 约束后的均值和标准差constrained_mean = slope * obs_mean + interceptconstrained_std = prediction_error * obs_std / np.std(constraint_var)# 计算不确定性削减original_std = ecs_values.std()uncertainty_reduction = (1 - constrained_std / original_std) * 100# 方法 2:使用 Skyborn 完整函数(适用于 xarray 数据)import xarray as xrfrom skyborn.calc import emergent_constraint_posterior# 将数据转换为 xarray.DataArrayconstraint_da = xr.DataArray( constraint_var, dims=['model'], coords={'model': [f'Model_{i+1:02d}'for i in range(n_models)]})ecs_da = xr.DataArray( ecs_values, dims=['model'], coords={'model': [f'Model_{i+1:02d}'for i in range(n_models)]})# 计算后验分布posterior_pdf, posterior_std, posterior_mean = emergent_constraint_posterior( constraint_data=constraint_da, target_data=ecs_da, constraint_grid=constraint_grid, target_grid=ecs_grid, obs_pdf=obs_pdf)步骤 5:可视化结果
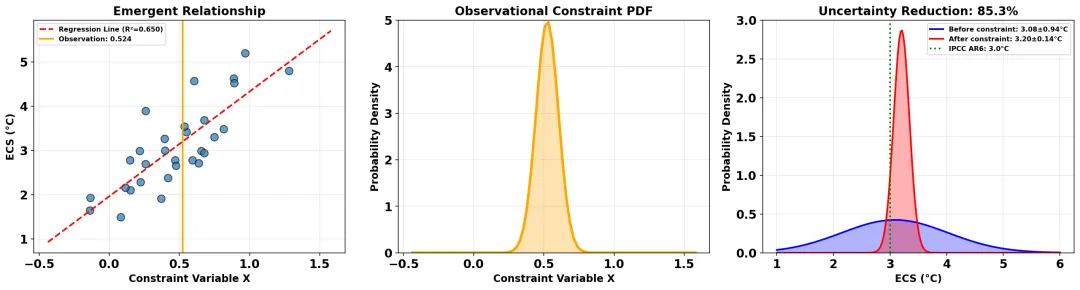
import matplotlib.pyplot as pltfig, axes = plt.subplots(1, 3, figsize=(18, 5))# 子图1:涌现关系ax = axes[0]ax.scatter(constraint_var, ecs_values, s=80, alpha=0.7, edgecolors='black')ax.plot(constraint_grid, slope * constraint_grid + intercept, 'r--', linewidth=2, label=f'Regression Line (R²={correlation**2:.3f})')ax.axvline(obs_mean, color='orange', linewidth=2, label=f'Observation: {obs_mean:.3f}')ax.set_xlabel('Constraint Variable X', fontsize=12)ax.set_ylabel('ECS (°C)', fontsize=12)ax.set_title('Emergent Relationship', fontsize=14, fontweight='bold')ax.legend()ax.grid(True, alpha=0.3)# 子图2:观测约束 PDFax = axes[1]ax.plot(constraint_grid, obs_pdf, color='orange', linewidth=3)ax.fill_between(constraint_grid, obs_pdf, alpha=0.3, color='orange')ax.set_xlabel('Constraint Variable X', fontsize=12)ax.set_ylabel('Probability Density', fontsize=12)ax.set_title('Observational Constraint PDF', fontsize=14, fontweight='bold')ax.grid(True, alpha=0.3)# 子图3:ECS 约束前后对比ax = axes[2]ecs_dense = np.linspace(1.0, 6.0, 200)original_pdf = gaussian_pdf(ecs_values.mean(), original_std, ecs_dense)constrained_pdf = gaussian_pdf(constrained_mean, constrained_std, ecs_dense)ax.plot(ecs_dense, original_pdf, 'b-', linewidth=2, label=f'Before constraint: {ecs_values.mean():.2f}±{original_std:.2f}°C')ax.fill_between(ecs_dense, original_pdf, alpha=0.3, color='blue')ax.plot(ecs_dense, constrained_pdf, 'r-', linewidth=2, label=f'After constraint: {constrained_mean:.2f}±{constrained_std:.2f}°C')ax.fill_between(ecs_dense, constrained_pdf, alpha=0.3, color='red')ax.axvline(3.0, color='green', linestyle=':', linewidth=2, label='IPCC AR6: 3.0°C')ax.set_xlabel('ECS (°C)', fontsize=12)ax.set_ylabel('Probability Density', fontsize=12)ax.set_title(f'Uncertainty Reduction: {uncertainty_reduction:.1f}%', fontsize=14, fontweight='bold')ax.legend()ax.grid(True, alpha=0.3)plt.tight_layout()plt.show()真实数据应用示例
对于真实的气候模式数据(如 CMIP6),流程类似:
import xarray as xrfrom skyborn.calc import emergent_constraint_posterior, pearson_correlation# 1. 加载多模式集合数据ds_models = xr.open_mfdataset('cmip6_models/*.nc', combine='nested', concat_dim='model')# 2. 提取约束变量和目标变量# 例如:低云反馈(LCC)与 ECSlcc = ds_models['low_cloud_cover'].mean(dim=['time', 'lat', 'lon'])ecs = ds_models['equilibrium_climate_sensitivity']# 3. 检查相关性r = pearson_correlation(lcc, ecs)# 4. 加载观测数据obs_lcc_mean = 0.45# 来自卫星观测obs_lcc_std = 0.02# 观测不确定性# 5. 应用涌现约束constraint_grid = np.linspace(lcc.min() - 0.1, lcc.max() + 0.1, 100)ecs_grid = np.linspace(1.5, 5.5, 100)obs_pdf = gaussian_pdf(obs_lcc_mean, obs_lcc_std, constraint_grid)posterior_pdf, posterior_std, posterior_mean = emergent_constraint_posterior( constraint_data=lcc, target_data=ecs, constraint_grid=constraint_grid, target_grid=ecs_grid, obs_pdf=obs_pdf)完整代码示例
以下是一个从数据准备到可视化的完整示例:
import numpy as npimport matplotlib.pyplot as pltfrom skyborn.calc import gaussian_pdf, pearson_correlation# ==================== 步骤 1: 准备数据 ====================np.random.seed(42)n_models = 30# 生成 ECS 值ecs_values = np.random.normal(3.2, 0.9, n_models)ecs_values = np.clip(ecs_values, 1.5, 5.5)ecs_values[0:3] = [2.1, 4.8, 5.2]# 生成约束变量constraint_strength = 0.7noise_level = np.sqrt(1 - constraint_strength**2)ecs_normalized = (ecs_values - ecs_values.mean()) / ecs_values.std()constraint_var = constraint_strength * ecs_normalized + noise_level * np.random.randn(n_models)constraint_var = constraint_var * 0.3 + 0.5# ==================== 步骤 2: 建立涌现关系 ====================correlation = pearson_correlation(constraint_var, ecs_values)slope, intercept = np.polyfit(constraint_var, ecs_values, 1)# ==================== 步骤 3: 设置观测约束 ====================obs_mean = constraint_var.mean() + 0.05obs_std = 0.08constraint_grid = np.linspace(constraint_var.min() - 0.3, constraint_var.max() + 0.3, 80)ecs_grid = np.linspace(1.5, 5.5, 80)obs_pdf = gaussian_pdf(obs_mean, obs_std, constraint_grid)# ==================== 步骤 4: 计算约束结果 ====================predicted_ecs = slope * constraint_var + interceptresiduals = ecs_values - predicted_ecsprediction_error = np.std(residuals)constrained_mean = slope * obs_mean + interceptconstrained_std = prediction_error * obs_std / np.std(constraint_var)original_std = ecs_values.std()uncertainty_reduction = (1 - constrained_std / original_std) * 100# ==================== 步骤 5: 绘制结果 ====================fig, axes = plt.subplots(1, 3, figsize=(18, 5))# 子图1:涌现关系ax = axes[0]ax.scatter(constraint_var, ecs_values, s=80, alpha=0.7, edgecolors='black')ax.plot(constraint_grid, slope * constraint_grid + intercept, 'r--', linewidth=2, label=f'Regression Line (R²={correlation**2:.3f})')ax.axvline(obs_mean, color='orange', linewidth=2, label=f'Observation: {obs_mean:.3f}')ax.set_xlabel('Constraint Variable X', fontsize=12)ax.set_ylabel('ECS (°C)', fontsize=12)ax.set_title('Emergent Relationship', fontsize=14, fontweight='bold')ax.legend()ax.grid(True, alpha=0.3)# 子图2:观测约束 PDFax = axes[1]ax.plot(constraint_grid, obs_pdf, color='orange', linewidth=3)ax.fill_between(constraint_grid, obs_pdf, alpha=0.3, color='orange')ax.set_xlabel('Constraint Variable X', fontsize=12)ax.set_ylabel('Probability Density', fontsize=12)ax.set_title('Observational Constraint PDF', fontsize=14, fontweight='bold')ax.grid(True, alpha=0.3)# 子图3:ECS 约束前后对比ax = axes[2]ecs_dense = np.linspace(1.0, 6.0, 200)original_pdf = gaussian_pdf(ecs_values.mean(), original_std, ecs_dense)constrained_pdf = gaussian_pdf(constrained_mean, constrained_std, ecs_dense)ax.plot(ecs_dense, original_pdf, 'b-', linewidth=2, label=f'Before constraint: {ecs_values.mean():.2f}±{original_std:.2f}°C')ax.fill_between(ecs_dense, original_pdf, alpha=0.3, color='blue')ax.plot(ecs_dense, constrained_pdf, 'r-', linewidth=2, label=f'After constraint: {constrained_mean:.2f}±{constrained_std:.2f}°C')ax.fill_between(ecs_dense, constrained_pdf, alpha=0.3, color='red')ax.axvline(3.0, color='green', linestyle=':', linewidth=2, label='IPCC AR6: 3.0°C')ax.set_xlabel('ECS (°C)', fontsize=12)ax.set_ylabel('Probability Density', fontsize=12)ax.set_title(f'Uncertainty Reduction: {uncertainty_reduction:.1f}%', fontsize=14, fontweight='bold')ax.legend()ax.grid(True, alpha=0.3)plt.tight_layout()plt.show()
详细的使用介绍方法在:https://skyborn.readthedocs.io/en/latest/notebooks/ecs_emergent_constraints_analysis.html
小结:让观测“发声”,让预测更稳
涌现约束法以朴素的统计-物理逻辑,将真实世界观测融入模式集合评估, 在不更改模式结构的前提下,实现对关键气候指标的不确定性收缩。
相关资源链接
完整文档:https://skyborn.readthedocs.io/ GitHub仓库:https://github.com/QianyeSu/Skyborn 问题反馈:https://github.com/QianyeSu/Skyborn/issues
往期回顾
Python | 台风GPI | Potential Intensity Python | 球面谐波 | 流函数 | 势函数 Python | Skyborn | 缺测值填充 Python | Skyborn | 空间趋势 | 快速计算
References
Zhou Baiquan,Zhai Panmao. 2021. The constraint methods for projection in the IPCC Sixth Assessment Report on climate change. Acta Meteorologica Sinica,79(6):1063-1070. DOI: 10.11676/qxxb2021.069
本文来自网友投稿或网络内容,如有侵犯您的权益请联系我们删除,联系邮箱:wyl860211@qq.com 。
