什么是随机森林算法,它的算法原理及代码实现?

大家好，我是小寒

今天给大家分享一个超强的算法模型，随机森林

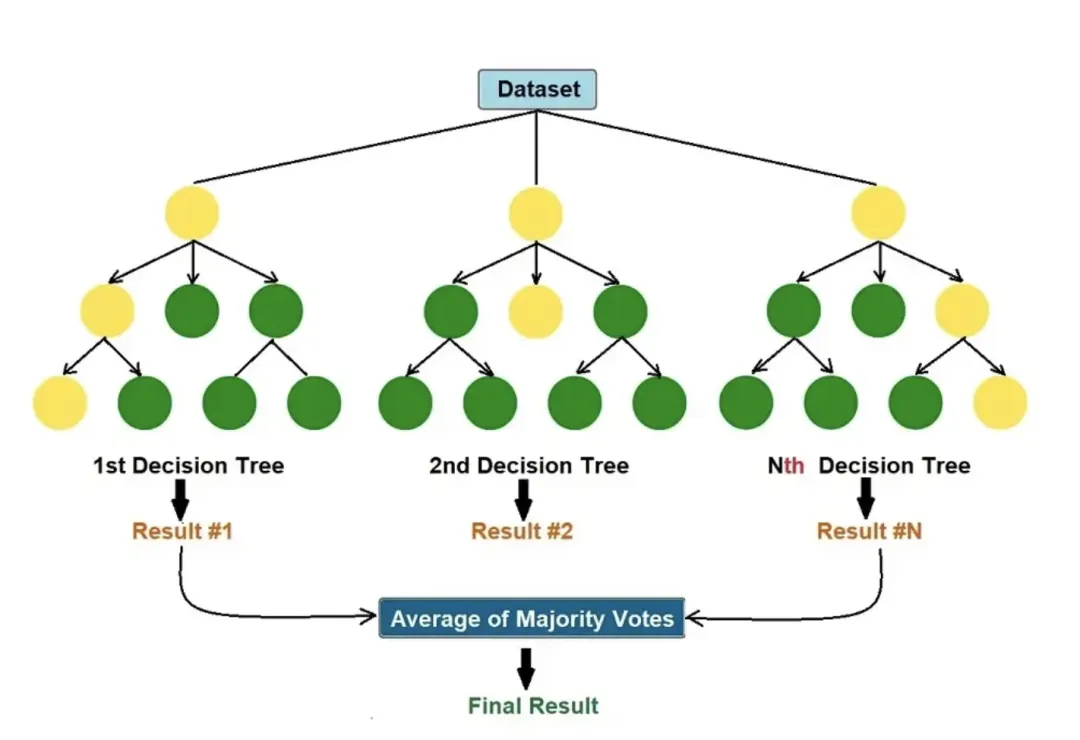
随机森林（Random Forest，简称 RF）是一种集成学习方法，主要用于分类和回归问题。

它通过构建多棵决策树，并结合多个树的输出结果来进行预测，旨在提高模型的精度，减少过拟合，并提高模型的稳定性。

基本原理

随机森林的强大源于两个关键的随机性，这使得森林中的每一棵树都各不相同，从而降低了模型的方差。

1.Bagging (Bootstrap Aggregating)

随机森林通过自助采样法从原始训练集中有放回地抽取  个样本。

这意味着有些样本会被多次选中，而有些则可能从未被选中（这些未被抽中的样本被称为 Out-of-Bag, OOB 样本，常用于评估模型性能）。

2.特征随机选择

在构建决策树的每个节点时，随机森林不会考虑所有的特征 ，而是从  个特征中随机选取  个特征（通常 ），并在其中选择最优的切分点。

这种方式使得每棵树的训练变得更加独立，降低了树与树之间的相关性，从而提高了模型的泛化能力。

通过样本随机化和特征随机化，随机森林能够极大地降低单棵决策树的方差（Variance），从而防止过拟合，并提高模型在未见数据上的泛化能力。

随机森林的构建过程

1. 数据抽样

   假设训练集有 N 个样本，随机森林通过有放回抽样（Bootstrap Sampling）从原始数据集中抽取多个子集，每个子集的大小也为 N。每个子集可能会包含重复的样本。剩下的未被抽中的样本组成 Out of Bag (OOB) 数据集，可以用来做交叉验证。

2. 构建决策树

   对每个训练子集，使用 CART 算法构建一棵决策树。

   在每个决策树的节点分裂时，随机选择 m 个特征（，其中 M 是特征总数），然后选择最佳特征进行分裂。

3. 预测

• 在分类问题中，使用多数投票的方式来汇总每棵树的预测结果，即选出票数最多的类别。
• 在回归问题中，使用所有树的预测结果的均值来做最终预测。

4. Out-of-Bag (OOB) 验证

   对于每棵树，未参与训练的样本（即OOB样本）可以用于评估模型的性能。

   这些样本在某棵树的训练过程中没有被用来训练，可以用来检验该树的泛化能力，从而为整个模型提供一个误差估计。

数学公式

假设我们有一个训练集 ，其中  是输入特征， 是输出标签。

1. 树的构建（决策树分裂）

   对于每棵决策树  的节点，选择一个特征子集 ，并基于该子集选择一个最佳划分特征。

   划分标准通常使用基尼指数（Gini Index）或信息增益（Information Gain）等。

• 基尼指数

  其中  是类  的概率（即类  在数据集  中的比例）。

• 信息增益

  其中， 表示数据集  的信息熵， 是特征  取值为  的子集。

2. 模型预测

   对于回归问题，随机森林的输出为所有树预测值的平均值

   其中， 是树的数量， 是第  棵树的预测值。

   对于分类问题，随机森林的输出是所有树的投票结果

   其中， 是第  棵树的预测类别，最终类别是票数最多的类别。

必会超参数

1. 树的数量 T：增加树的数量可以提高模型的稳定性和准确性，但也会增加计算成本。
2. 树的最大深度：控制每棵树的最大深度，可以避免过拟合。
3. 每次分裂时选择的特征数量 m：增加特征数量会使得模型更加复杂，减小 m 可以提高树之间的多样性。
4. 最小样本分裂数：控制每个节点最小样本数，有助于防止过拟合。

随机森林的优点

• 减少过拟合：通过随机采样和随机选择特征，随机森林有效地减少了单棵决策树可能产生的过拟合问题。
• 处理大规模数据：随机森林能够高效处理大规模数据集，并且可以处理大量特征。
• 并行化处理：每棵树的生成是独立的，非常适合在大规模分布式环境下运行。
• 鲁棒性：即使某些数据点有噪声，随机森林通常依然能够保持较高的准确率。
• 自动估计特征重要性：随机森林能够给出每个特征的重要性，帮助特征选择。

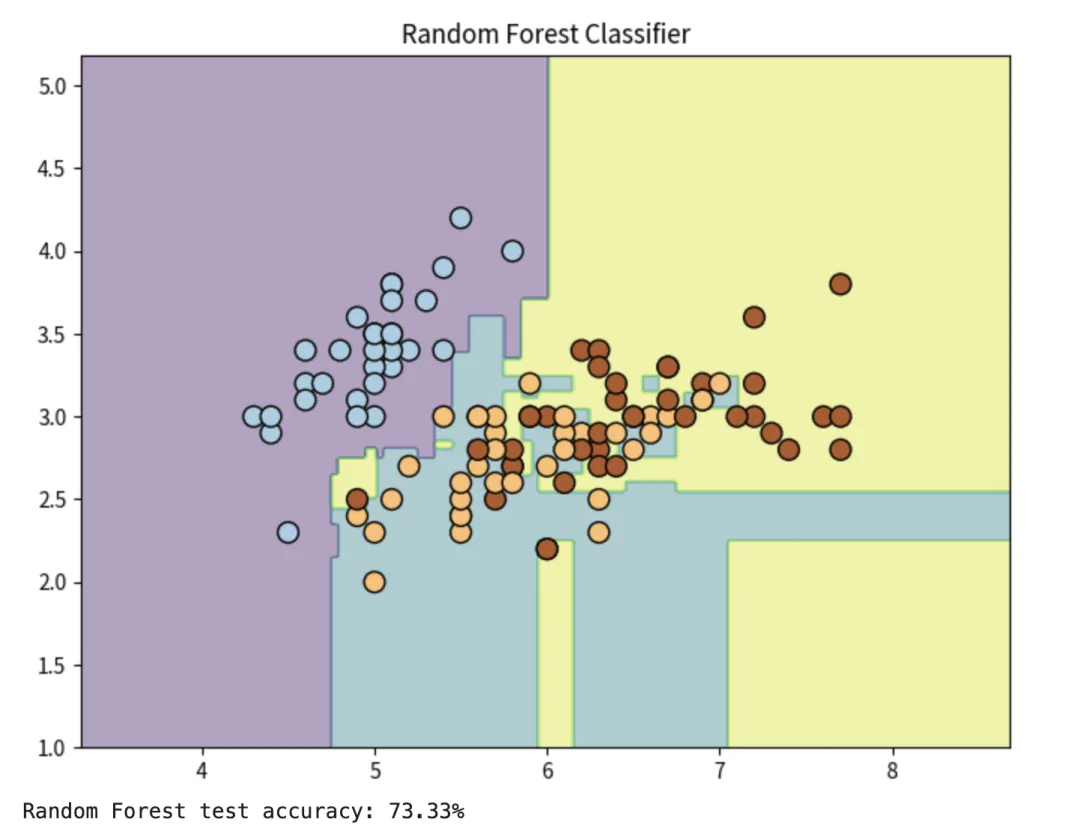
案例分享

下面是一个使用随机森林算法进行分类的具体示例代码。

# 导入所需库import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import load_irisfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.model_selection import train_test_splitfrom sklearn.decomposition import PCA# 加载Iris数据集iris = load_iris()X = iris.data[:, :2]  # 只使用前两个特征y = iris.target# 数据划分：训练集与测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建随机森林分类器rf = RandomForestClassifier(n_estimators=10, random_state=42)rf.fit(X_train, y_train)# 绘制决策边界def plot_decision_boundary(X, y, model, ax):    h = .02  # 网格步长    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),                         np.arange(y_min, y_max, h))    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])    Z = Z.reshape(xx.shape)# 绘制背景色    ax.contourf(xx, yy, Z, alpha=0.4)    ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=100, cmap=plt.cm.Paired)    ax.set_title("Random Forest Classifier")# 设置画布fig, ax = plt.subplots(figsize=(8, 6))# 绘制随机森林的决策边界plot_decision_boundary(X_train, y_train, rf, ax)# 显示结果plt.show()# 打印测试集准确率print("Random Forest test accuracy: {:.2f}%".format(rf.score(X_test, y_test) * 100))