有限元 | Python画三维框架的弯矩图

一般情况下，梁单元每个结点的位移具有6个自由度，它对应于6个结点力。在系统中取出结点为i和j的梁单元，如图1所示。取右手坐标系，x轴为单元轴线方向，而y轴和z轴为截面的主惯性轴。

▲图1

三维梁单元的内力是基于杆的位置的函数,由一系列的离散点组成矩阵

在画某一单元的变形或内力图时，通常是以该单元起点为总体坐标系的坐标原点，杆轴沿着总体坐标系的轴正方向，杆轴上的离散点便是矩阵A的第一行，离散点对应的函数值便是矩阵A的第二行。这是默认图形在面上，如果将图形画在面上，矩阵A的第二行全为0

▲图2

用python演示图2的框架，在初始位置不同的平面内的弯矩图

import matplotlib.pyplot as pltimport numpy as npdefmain():    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']    # 这个字体能够支持中英文字符    plt.rcParams['axes.unicode_minus'] = False# 正常显示负号# 三维框架    xs = [0,0,0,1]    ys = [0,0,2,2]    zs = [0,2,2,2]    xx = np.linspace(0, 2, 10)      # 梁单元划分为10个小段# 每一个离散点的弯矩值    m = [0.5,0.5, 0.5, 0.5, 0.5,0.5,0.5, 0.5, 0.5, 0.5]    xx1 = np.hstack( (xx[0], xx, xx[-1]) )    m1 = np.hstack( (xx[0],m, xx[0]) )    zeros = np.zeros(12)# 图形在xoy面，故第三行全为0    A = np.vstack( ( xx1,  m1, zeros) )# 图形在xoz面，故第二行全为0    A1 = np.vstack( ( xx1, zeros, m1) )    fig,  axs = plt.subplots(nrows=1, ncols=2, sharex=True,                                    figsize=(8, 4),subplot_kw={"projection": "3d"})# 绘制刚架图    axs[0].plot(xs, ys, zs)# 绘制单元1在xoy面的弯矩图    axs[0].plot( A[0,:],A[1,:],A[2,:])    axs[0].set( title='xoy面的弯矩图')    axs[0].set_xlim(-0.4, 2)# 绘制单元1在xoz面的弯矩图    axs[1].plot(xs, ys, zs)    axs[1].plot(A1[0,:], A1[1,:], A1[2,:] )    axs[1].set( title='xoz面的弯矩图')    axs[1].set_xlim(-0.4, 2)    fig.savefig("z216.png",dpi=300)    plt.show()if __name__ == "__main__":    main() 

▲图3

内力图要经过旋转、平移操作，使之回到对应的位置上去，即图形与局部坐标一致。对于图1中的单元1，则需要作两次旋转操作(RA)，而单元2则需要作旋转平移操作(TA)。缩放操作则根据图形是否协调适当考虑。下面动手画图2中的各单元扭矩图(绕单元轴线的弯矩)

单元1的两次旋转操作

import matplotlib.pyplot as pltimport numpy as npdefmain():    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']    # 这个字体能够支持中英文字符    plt.rcParams['axes.unicode_minus'] = False# 正常显示负号# 三维框架    xs = [0,0,0,1]    ys = [0,0,2,2]    zs = [0,2,2,2]    xx = np.linspace(0, 2, 10)      # 梁单元划分为10个小段# 每一个离散点的弯矩值    m = [0.5,0.5, 0.5, 0.5, 0.5,0.5,0.5, 0.5, 0.5, 0.5]    xx1 = np.hstack( (xx[0], xx, xx[-1]) )    m1 = np.hstack( (xx[0],m, xx[0]) )    ones = np.ones(12)    zeros = np.zeros(12)# 矩阵A增加维度，即第四行全为1,图形在xoz面，故第二行全为0    A = np.vstack( ( xx1, zeros, m1, ones) )# z轴旋转矩阵    Rz = np.array([[0, -1,  0, 0],                  [1,  0,  0, 0],                  [0,  0,  1, 0],                  [0,  0,  0, 1]  ])# x轴旋转矩阵    Rx = np.array([[1, 0, 0, 0],                  [0, 0, -1, 0],                  [0, 1,  0, 0],                  [0, 0, 0, 1]  ])# 旋转变换    Rxyz = Rz @ A    Rxyz1 = Rx @ Rxyz    fig,  axs = plt.subplots(nrows=2, ncols=2, sharex=True,                                    figsize=(8, 8),subplot_kw={"projection": "3d"})# 绘制刚架图    axs[0,0].plot(xs, ys, zs)# 绘制单元1未旋转时的弯矩图    axs[0,0].plot( xx1,zeros,m1)    axs[0,0].set( title='旋转前的弯矩图')    axs[0,0].set_xlim(-0.4, 2)# 绘制单元1绕z轴旋转后的弯矩图    axs[0,1].plot(xs, ys, zs)    axs[0,1].plot(Rxyz[0,:], Rxyz[1,:], Rxyz[2,:] )    axs[0,1].set( title='绕Z轴旋转后的弯矩图')    axs[0,1].set_xlim(-0.4, 2)# 绘制单元1绕x轴旋转后的弯矩图    axs[1,0].plot(xs, ys, zs)    axs[1,0].plot(Rxyz1[0,:], Rxyz1[1,:], Rxyz1[2,:] )    axs[1,0].set( title='绕X轴旋转后的弯矩图')    axs[1,0].set_xlim(-0.4, 2)    fig.savefig("z211.png",dpi=300)    plt.show()if __name__ == "__main__":    main() 

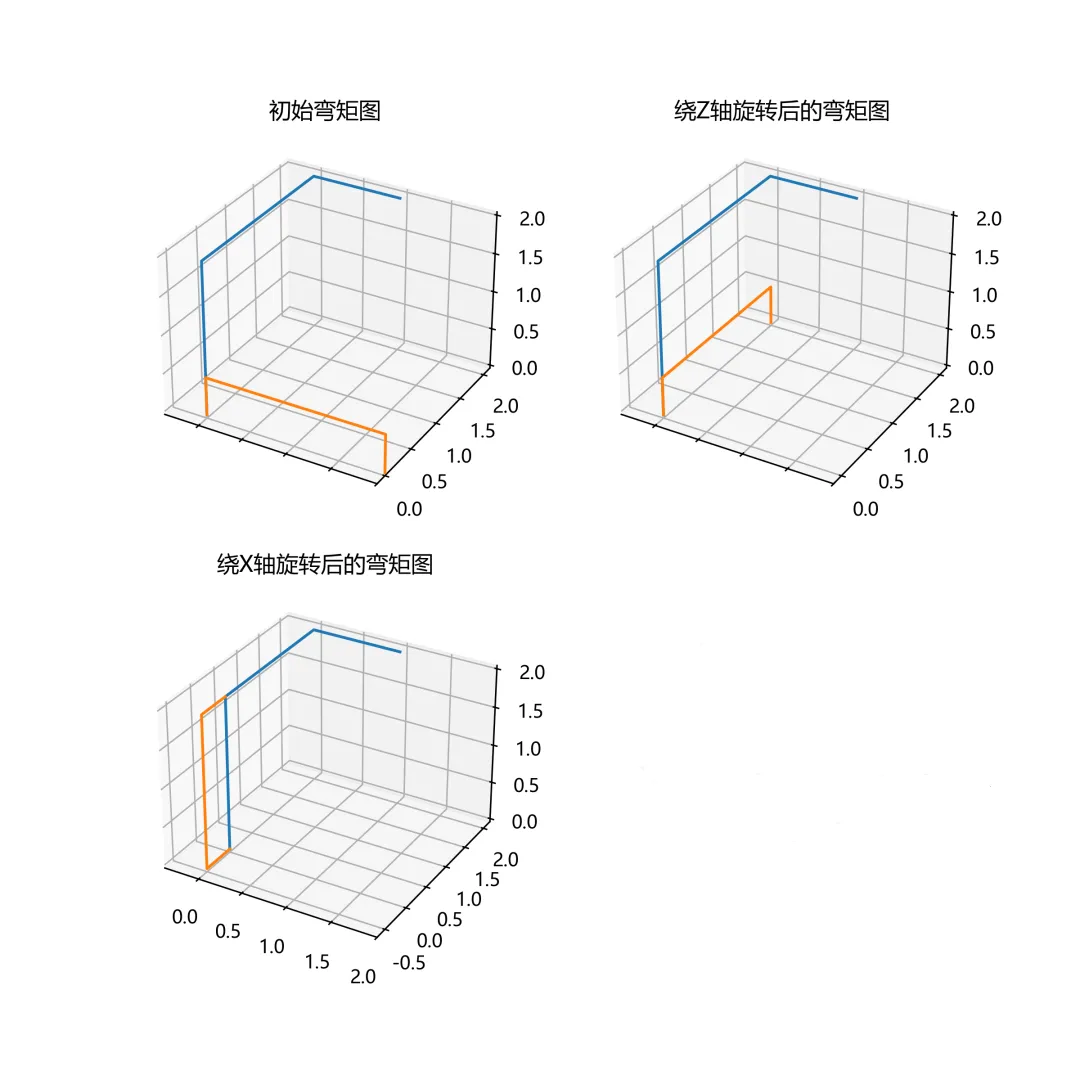
▲图4

单元2的旋转平移操作

import matplotlib.pyplot as pltimport numpy as npdefmain():    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']    # 这个字体能够支持中英文字符    plt.rcParams['axes.unicode_minus'] = False# 正常显示负号# 三维框架    xs = [0,0,0,1]    ys = [0,0,2,2]    zs = [0,2,2,2]    xx = np.linspace(0, 2, 10)      # 梁单元划分为10个小段# 每一个离散点的弯矩值    m = [0.5,0.5, 0.5, 0.5, 0.5,0.5,0.5, 0.5, 0.5, 0.5]    xx1 = np.hstack( (xx[0], xx, xx[-1]) )    m1 = np.hstack( (xx[0],m, xx[0]) )    ones = np.ones(12)    zeros = np.zeros(12)# 矩阵A增加维度，即第四行全为1.图形在xoz面，故第二行全为0    A = np.vstack( ( xx1,zeros,m1, ones) )# z轴旋转矩阵    Rz = np.array([[0, -1,  0, 0],                  [1,  0,  0, 0],                  [0,  0,  1, 0],                  [0,  0,  0, 1]  ])# 平移矩阵    T =  np.array([[1, 0,  0, 0],                  [0,  1,  0, 0],                  [0,  0,  1, 2],                  [0,  0,  0, 1]  ])# 旋转平移变换    Rxyz = Rz @ A    Rxyz1 = T @ Rxyz    fig,  axs = plt.subplots(nrows=2, ncols=2, sharex=True,                                    figsize=(8, 8),subplot_kw={"projection": "3d"})# 绘制刚架图    axs[0,0].plot(xs, ys, zs)# 绘制单元2未旋转时的弯矩图    axs[0,0].plot( xx1,zeros,m1)    axs[0,0].set( title='旋转前的弯矩图')    axs[0,0].set_xlim(-0.4, 2)# 绘制单元2旋转后的弯矩图    axs[0,1].plot(xs, ys, zs)    axs[0,1].plot(Rxyz[0,:], Rxyz[1,:], Rxyz[2,:] )    axs[0,1].set( title='旋转后的弯矩图')    axs[0,1].set_xlim(-0.4, 2)# 绘制单元2平移后的弯矩图    axs[1,0].plot(xs, ys, zs)    axs[1,0].plot(Rxyz1[0,:], Rxyz1[1,:], Rxyz1[2,:] )    axs[1,0].set( title='平移后的弯矩图')    axs[1,0].set_xlim(-0.4, 2)    fig.savefig("z22.png",dpi=300)    plt.show()if __name__ == "__main__":    main()  

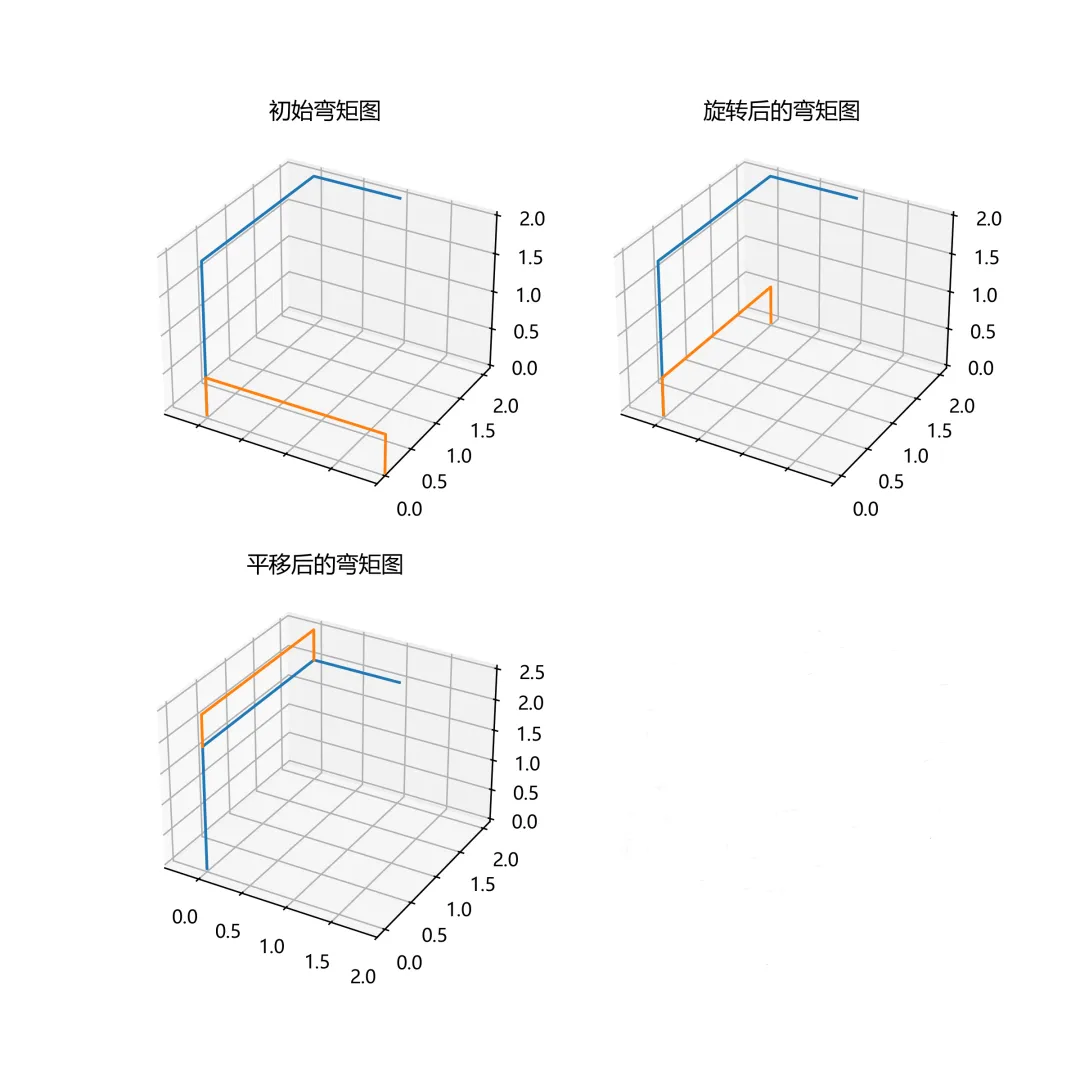
▲图5

实际上，扭矩图和轴力图一样，图形位置都可以自行定义。

附录：

三维空间中绕轴旋转的旋转矩阵分别为

平移矩阵为