当前位置：首页>python>我的Python100天打卡:57/100

我的Python100天打卡:57/100

2026-02-05 00:41:22

#鸢尾花数学大系

挑战100天持续练习Python

今天是第57天

---

上次笔记，完成了第十五章Numpy的常见运算的15.3部分，承接15.2“Numpy广播原则”的部分，练习了如何使用Numpy进行统计运算。

今天继续挑战第十五章，目标是把整个第十五章结束。具体内容包括：

15.4 Numpy库中的常见函数

练习Q15-1 给定一元高斯函数，给出固定参数值，用Numpy和matplotlib可视化函数图像（线图）。

练习Q15-2 给定二元高斯函数，用Numpy和matplotlib可视化函数图像（三维曲面图）。

练习Q15-3 给出二元高斯分布的概率密度函数，给出特定参数值，用Numpy和matplotlib可视化函数图像（等高线图）。

15.4 Numpy库中的常见函数

1️⃣自定义函数的代码：

import numpy as npimport matplotlib.pyplot as plt# 自定义可视化函数def visualize_fx(x_array, f_array, title, step = False):    fig, ax = plt.subplots(figsize = (5,5))    ax.plot([-5,5],[-5,5], c = 'r', ls = '--', lw = 0.5)    if step:    # 使用“步长”绘图        ax.step(x_array, f_array)       else:      # 使用“光滑的点”绘图        ax.plot(x_array, f_array)    ax.set_xlim(-5, 5)    ax.set_ylim(-5, 5)    ax.axvline(0, c = 'k')    ax.axhline(0, c = 'k')    ax.set_xticks(np.arange(-5, 5+1))    ax.set_yticks(np.arange(-5, 5+1))          ax.set_xlabel('x')    ax.set_ylabel('f(x)')    plt.grid(True)    ax.set_aspect('equal', adjustable='box')    fig.savefig(title + '.svg', format='svg')

调用函数的代码：

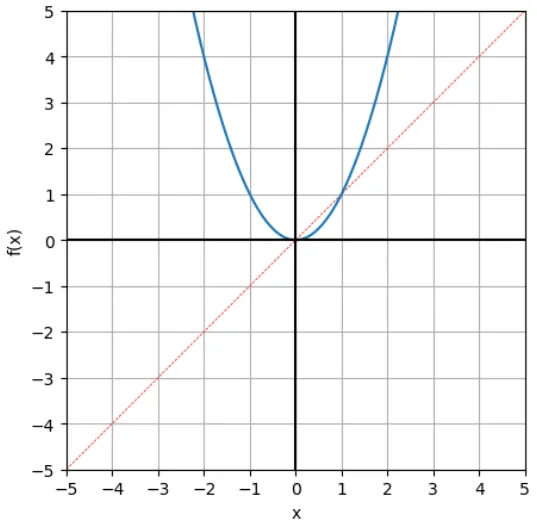
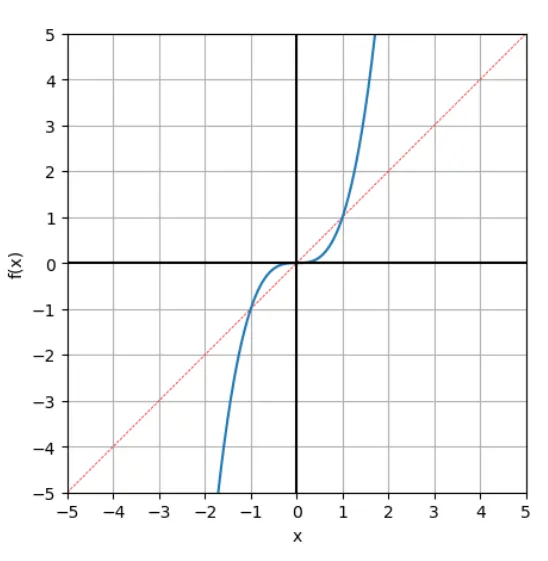
# 幂函数，p = 2x_array = np.linspace(-5,5,1001)f_array = np.power(x_array, 2)visualize_fx(x_array, f_array, '幂函数_p=2')# 幂函数，p = 3f_array = np.power(x_array, 3)visualize_fx(x_array, f_array, '幂函数_p=3')

2️⃣可视化结果（示例）

1. 幂函数，p=2：

2. 幂函数，p=3：

3️⃣特殊注意点：

（1）部分程序根据实际需求，需要使用到“step方法”（这部分在主体自定义函数中，已经用了“if语句”来判断是否需要，因此避免了后续调用函数时再进行判断的的麻烦）:

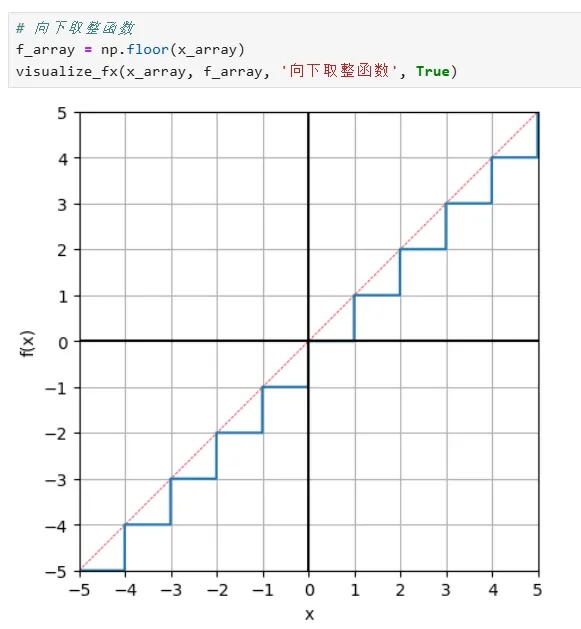
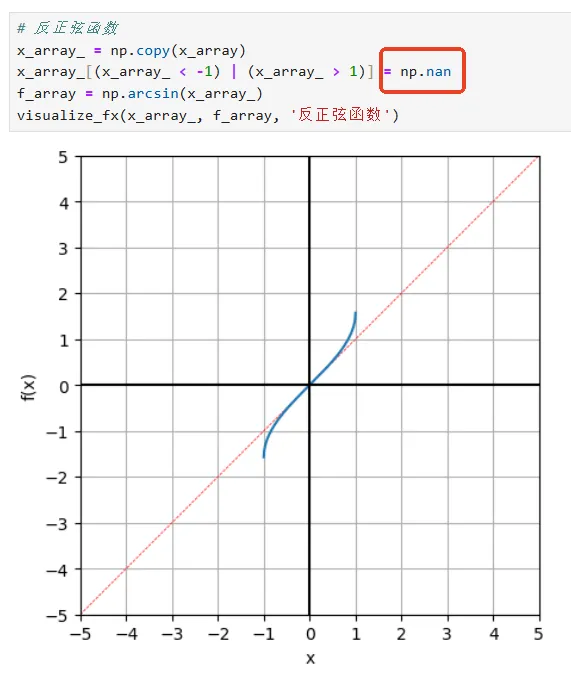
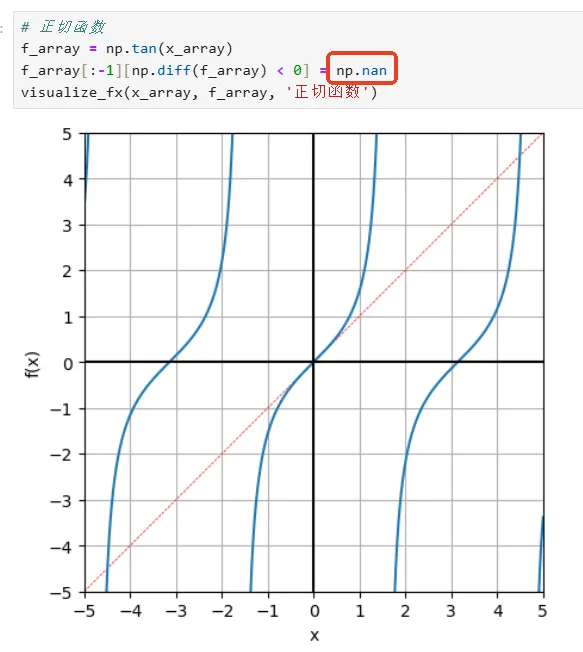
（2）部分程序需要设置某些特殊点为“nan”，或者设置取数范围，以免Numpy报错，或不美观：

学完15.4，感觉像是刚好热了个身~

那么趁热打铁，马上来三道练习题，巩固一下第十五章Numpy运算的知识：

练习Q15-1 给定一元高斯函数，给出固定参数值，用Numpy和matplotlib可视化函数图像（线图）。

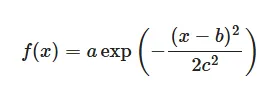
1️⃣思考过程及#完整代码：

# 练习Q15-1 给定一元高斯函数，给出固定参数值，用Numpy和matplotlib可视化函数图像（线图）。# 以下是AI给我思考过程：# === 步骤1: 导入必要的库 ===import numpy as np   # 计算import matplotlib.pyplot as plt   # 绘图# === 步骤2: 定义函数参数 ===# 根据题目，参数值为：a=1, b=2, c=1 （题目给定的）a = 1b = 2c = 1# === 步骤3: 创建x轴数据 ===# 思考：使用什么“工具”？（.linspace()） # 我们需要在哪个范围内采样x值？(-6, 6) # 取多少个点比较合适？(121)x_array = np.linspace(-6, 6, 121)# === 步骤4: 计算y轴数据 ===# 这是最关键的一步！需要将数学公式转换为NumPy代码# 公式：f(x) = a * exp(-(x - b)² / (2 * c²))# 分步计算（帮助理解）：# 1. 先计算 (x - b)diff = x_array - b# 2. 计算 (x - b)²diff_squared = diff ** 2    # 【填上正确的幂次】# 3. 计算分母 2 * c²denominator = 2 * (c ** 2 )  # 【填上正确的幂次】# 4. 计算指数部分：-diff_squared / denominatorexponent = -diff_squared / denominator# 5. 计算整个函数值f_x_array = a * np.exp(exponent)  # 【填上正确的NumPy函数(.exp())】# 注意：.exp()这个函数表示以 e（自然常数）为底数，x为指数的幂运算。# 也可以一步完成（挑战！）：# f_x_array = a * np.exp(-((x_array - b) ** 2 ) / (2 * c ** 2 ))# === 步骤5: 创建图形 ===# 思考：图形尺寸设置为多少合适？(6, 4)fig, ax = plt.subplots(figsize=(6, 4))# 绘制线图# 思考：plot函数需要什么参数？(x = x_array; y = f(x_array))ax.plot(x_array, f_x_array)  # 【填写x和y的数据(注意y轴的表达方式，妙呀)】# === 步骤6: 设置坐标轴 ===# 设置x轴范围# 思考：为什么设置为-5到5而不是-6到6？（因为x轴用不上-6和6的区域吗？这样可以使得画面更集中？）ax.set_xlim(-5, 5)  # 【填写x轴范围】# 设置y轴范围# 思考：为什么y轴从0开始？# 思考：为什么要用f_x_array.max()作为上限？（因为这样可以不用人为操控y轴的上限吗？）ax.set_ylim(0, f_x_array.max())  # 【填写正确的方法】# === 步骤7: 添加标签和网格 ===# 设置x轴标签ax.set_xlabel('x')  # 【填写标签文本】# 设置y轴标签ax.set_ylabel('f(x)')  # 【填写标签文本】# 添加网格plt.grid()  # 【填写正确的方法】# === 步骤8: 显示图形 ===plt.show()

2️⃣运行结果：

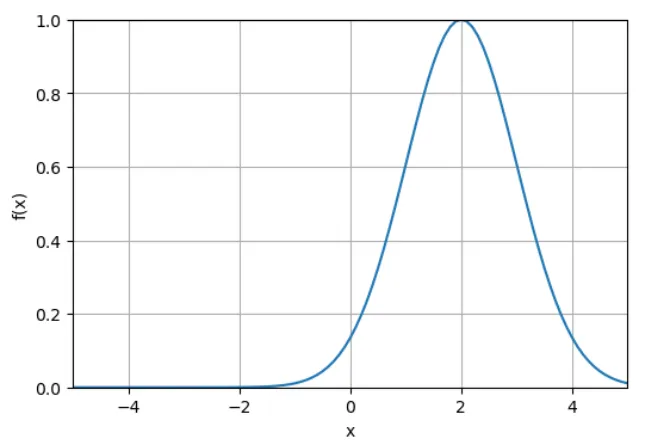
3️⃣心得：难点在于如何将“数学公式”转换为Numpy的表述。AI在这点做得很好：【先分步】，将公式拆成一小段、一小段，每段都简单得不得了；再将他们组合在一起，便成为了完整的公式。这样将大问题拆分为小问题的思想，不就是一种典型的计算思维么~挺好的挺好的。

练习Q15-2 给定二元高斯函数，用Numpy和matplotlib可视化函数图像（三维曲面图）。

1️⃣思考过程及#完整代码：

# === 步骤1: 导入必要的库 ===import numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3D  # 导入3D绘图模块# === 步骤2: 创建x1和x2的数据点 ===# 创建x1数组，范围-3到3，包含301个点x1_array = np.linspace(-3, 3, 301)  # 【填空：点数量】# 创建x2数组，同样的范围和点数x2_array = np.linspace(-3, 3, 301)  # 【填空：起始值和结束值】# === 步骤3: 生成网格 ===# 思考：为什么要用meshgrid？它返回什么？-> meshgrid将两个一维数组转换为二维网格xx1, xx2 = np.meshgrid(x1_array, x2_array)  # 【填空：函数名】# 打印验证形状print(f"xx1的形状: {xx1.shape}")print(f"xx2的形状: {xx2.shape}")# === 步骤4: 计算函数值 ===# 根据公式 f(x1,x2) = exp(-x1² - x2²) 计算ff = np.exp( -xx1**2 - xx2**2 )    # 别忘了.exp前面的“np”# === 步骤5: 创建三维图形 ===# 创建图形对象fig = plt.figure(figsize=(10, 8))# 添加3D子图# 思考：为什么用projection参数？-> 因为要设置投影类型啊ax = fig.add_subplot(projection='3d')  # 【填空：子图位置和投影类型】# === 步骤6: 绘制三维曲面 ===# 使用plot_wireframe绘制网格曲面# 思考：rstride和cstride参数的作用是什么？-> 它们控制网格的密度，值越大网格越稀疏ax.plot_wireframe(xx1, xx2, ff,                   rstride=10,  # 【填空：行步长】                  cstride=10,  # 【填空：列步长】                  color='blue',  # 网格线颜色                  linewidth=0.5,  # 网格线宽度                  alpha=0.8)  # 透明度# === 步骤7: 设置坐标轴标签 ===# 设置x轴标签，使用LaTeX公式表示ax.set_xlabel(r'$x_1$', fontsize=12)# 设置y轴标签ax.set_ylabel(r'$x_2$', fontsize=12)  # 【填空：变量名】# 设置z轴标签(f(x_1, x_2))ax.set_zlabel(r'$f(x_1, x_2)$', fontsize=12)# 设置标题ax.set_title('$f(x_1,x_2)=e^{-x_1^2-x_2^2}$', fontsize=14, fontweight='bold')# === 步骤8: 调整图形布局和视角 ===# 调整布局plt.tight_layout()# 设置视角（可选，但可以让图形更好看）# 思考：elev和azim参数分别控制什么？# 提示：elev是仰角，azim是方位角ax.view_init(elev=25, azim=-60)  # 调整视角# === 步骤9: 显示图形 ===plt.show()

2️⃣运行结果：

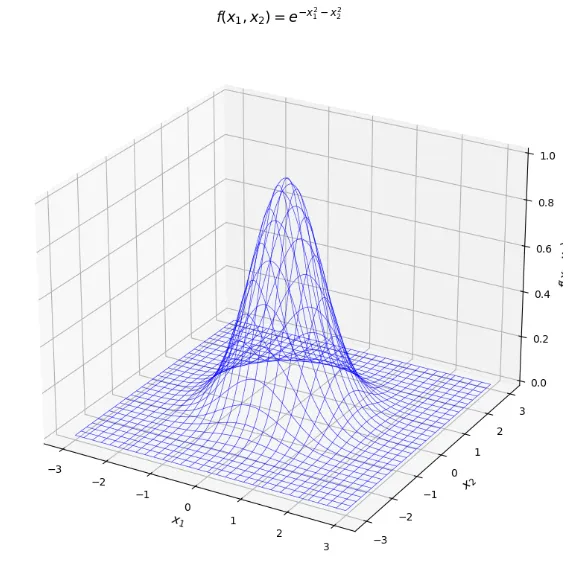
3️⃣心得：

1. 公式的“翻译”部分和第一题类似，注意.exp()前面要加上“np”，而不是直接使用，否则会报错（数学公式和numpy语法之间还是有区别的）。

2. 三维图表中，注意z轴的命名和其含义~

练习Q15-3 给出二元高斯分布的概率密度函数，给出特定参数值，用Numpy和matplotlib可视化函数图像（等高线图）。

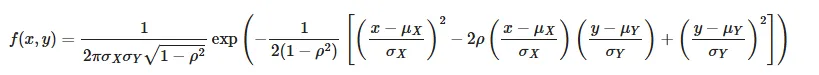
1️⃣思考过程及#完整代码：

这是一个看起来很复杂的公式，如果没有前面两道题的铺垫，我肯定被吓到。不过，有了AI的帮助，我不会慌的，按部就班来解决吧：

# === 步骤1: 导入必要的库 ===import numpy as npimport matplotlib.pyplot as pltimport matplotlibmatplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'SimSun']matplotlib.rcParams['axes.unicode_minus'] = False# === 步骤2: 设置参数 ===# 根据题目要求设置参数值（这部分题目已经给出了具体数值）# 提示：通常均值设为0，标准差设为1，相关系数设为某个值mu_X = 0   # 【填空：x的均值】mu_Y = 0   # 【填空：y的均值】sigma_X = 1  # 【填空：x的标准差】sigma_Y = 1  # 【填空：y的标准差】rho_XY = 0.6  # 【填空：相关系数】# === 步骤3: 创建网格数据 ===# 创建x和y的取值数组# 思考：范围应该多大？取多少个点？# 提示：通常范围是[-3, 3]或根据标准差决定x_array = np.linspace(-3, 3, 201)  # 【填空：点数量，如201】y_array = np.linspace(-3, 3, 201)  # 【填空：同样的点数量】# 生成网格，用meshgridxx1, xx2 = np.meshgrid(x_array, y_array)  # 【填空：网格生成函数】# === 步骤4: 定义概率密度函数 ===def f_XYPDF(xx1, xx2, sigma_X, sigma_Y, rho_XY, mu_X, mu_Y):    """    计算二元高斯分布的概率密度    参数:        xx1, xx2: 网格坐标        其他: 分布参数    """    # 4.1 计算归一化系数（公式左边比较复杂的“分数”部分）    # 公式中的系数: 1/(2π * σ_X * σ_Y * √(1-ρ²))    # 下面就是将公式“翻译”为Numpy代码的过程    coeff = 2 * np.pi * sigma_X * sigma_Y * np.sqrt(1 - rho_XY**2)    coeff = 1 / coeff  # 【填空：计算倒数】    # 4.2 标准化变量    # 将xx1标准化: (x - μ_X)/σ_X    xx1_std = (xx1 - mu_X) / sigma_X  # 【填空：分母】    xx2_std = (xx2 - mu_Y) / sigma_Y  # 【填空：分母】    # 4.3 计算椭圆项（指数部分）    # 公式: 1/(1-ρ²) * [xx1_std² - 2ρ*xx1_std*xx2_std + xx2_std²]    ellipse = 1/(1 - rho_XY**2) * (        xx1_std**2 - 2 * rho_XY * xx1_std * xx2_std + xx2_std**2    )    # 4.4 计算概率密度(即将公式两边的数，用“np.exp”链接在一起)    PDF = coeff * np.exp(-1/2 * ellipse)  # 【填空：指数函数】    return PDF# === 步骤5: 计算概率密度 ===# 调用函数计算整个网格上的概率密度PDF_ff = f_XYPDF(xx1, xx2, sigma_X, sigma_Y, rho_XY, mu_X, mu_Y)# === 步骤6: 创建图形 ===# 创建图形和坐标轴fig, ax = plt.subplots(figsize=(8, 6))  # 【填空：图形尺寸，如(8, 6)】# === 步骤7: 绘制等高线图 ===# 使用contourf绘制填充等高线图contour = ax.contourf(xx1, xx2, PDF_ff,                       levels=20,  # 等高线数量                      cmap='viridis')  # 颜色映射# === 步骤8: 添加颜色条 ===# 添加颜色条显示数值对应关系cbar = fig.colorbar(contour, ax=ax)cbar.set_label('概率密度', fontsize=12)# === 步骤9: 设置坐标轴 ===# 设置x轴范围ax.set_xlim(-3, 3)# 设置y轴范围ax.set_ylim(-3, 3)# 设置坐标轴标签ax.set_xlabel('x', fontsize=12)ax.set_ylabel('y', fontsize=12)# 添加标题ax.set_title('二元高斯分布概率密度函数 bivariate Gaussian distribution probability density function(PDF)', fontsize=14, fontweight='bold')# === 步骤10: 添加网格和设置比例 ===# 添加网格ax.grid(True, alpha=0.3, linestyle='--')# 设置等比例，保证图形不变形ax.set_aspect('equal', adjustable='box')# 标记均值点ax.plot(mu_X, mu_Y, 'ro', markersize=8, label=f'均值点({mu_X},{mu_Y})')ax.legend()# === 步骤11: 显示图形 ===plt.tight_layout()plt.show()

2️⃣运行结果：

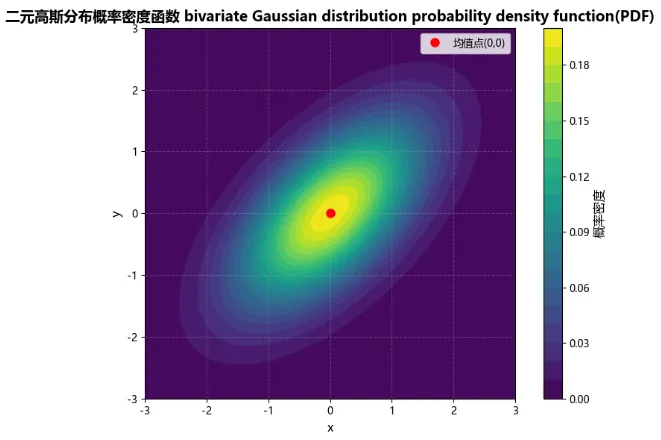
3️⃣心得：

1. 先感慨一下，运行结果好浪漫啊，像在宇宙中漂浮着。

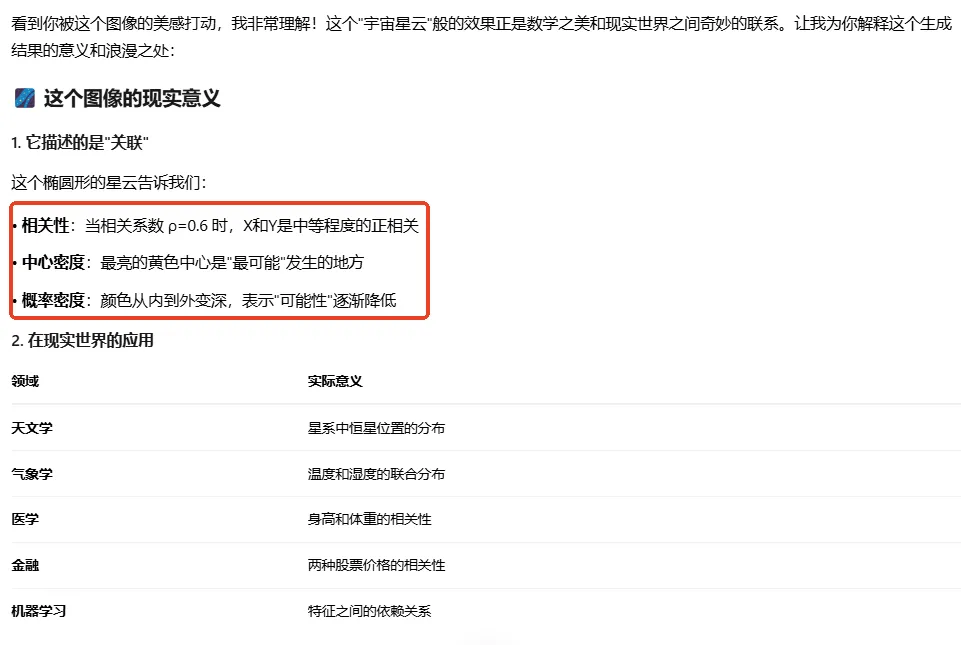
2. 二元高斯分布的函数，看起来很复杂，但其实用“拆分法”，也是一步步拆出来简单的部分，原来也不难嘛！很能提升一个人的自信心！

话说今天学习笔记的风格，又换了一下🤣：

1️⃣不再纠结代码的具体实现，因为都比较熟悉了。我觉得今天是从“抠细节”再到“看大局”的初步转变。

2️⃣学会利用已有的资源，加速、加深理解。如：

（1）先浏览作者本身在B站上发布的讲解视频，对整个第15章有了更清晰的全面认知（包括不限于：numpy常见运算有什么用？怎么用？用的时候有哪些注意的点？为什么要特别强调广播机制（因为各种拉伸都有它的份）？常见函数的可视化为什么用到step方法和nan参数来画图？），看完这个视频，再通过我整理的上面这些问题串起来，就像一道闪电穿过我的脑子，脉络瞬间变得清晰了：

【Chapter 15 NumPy常见运算 | 《编程不难》 | 鸢尾花书：从加减乘除到机器学习】https://www.bilibili.com/video/BV1mZ421h7u7/