今天这道题是2022蓝桥杯的原题，在本文中，将演示从“数学模型”到“代码编程”的思考过程，以及如何通过数形结合来简化建模过程。
核心解题思路
1. 暴力枚举
双重循环枚举所有数对，外层枚举a1...an的每一个元素，内层枚举ai身后的每一个数。
当 n 达到 2×10⁵ 时，计算量会达到 4×10¹⁰，必然超时。本题用暴力枚举只能得到30%的分数。
暴力枚举代码 ⬇️
#include<bits/stdc++.h>using namespace std;long long a[200002];intmain(){ int n; cin >> n; for(int i=1; i<=n; i++) { cin >> a[i]; } long long ans = 0; for(int i=1; i<=n; i++) { for(int j=i+1; j<=n; j++) { ans += a[i]*a[j]; } } cout << ans; return 0;}
2. 数学优化解法：代数变形
已知：(a₁ + a₂ + … + aₙ)² = a₁² + a₂² + … + aₙ² + 2S
移项可得：S = [ (总和)² - (平方和) ] / 2
这样，我们只需要遍历数组两次：
- 3) 代入公式得到
S = (sum * sum - sum_sq) / 2
时间复杂度直接降到 O(n)，完美适配 n ≤ 2×10⁵ 的数据规模。
3. 数学优化解法：数形结合
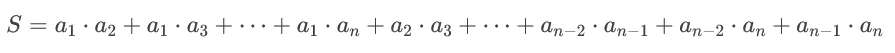从S的定义来看，S等于每一个数，和其身后每一个数相乘得到一个值，然后进行累加。
构造一个如下图所示的矩阵，每个方块的值是行与列对应的值相乘，黄色部分覆盖的范围值之后就是S（注意，红色部分覆盖的值之后也是S）。
所以，2*S = (a1+a2+a3+a4+a5)*(a1+a2+a3+a4+a5)-(a1*a1+a2*a2+a3*a3+a4*a4+a5*a5)
推导的结果和代数解法得到的结果是一致的。
优化代码
#include<bits/stdc++.h>using namespace std;long long a[200002];intmain(){ int n; cin >> n; for(int i=1; i<=n; i++) { cin >> a[i]; } long long ans = 0; long long sumr = 0, djx=0; for(int i=1; i<=n; i++) { sumr += a[i]; djx += a[i]*a[i]; } for(int i=1; i<=n; i++) { ans += sumr*a[i]; } ans -= djx; ans /= 2; cout << ans; return 0;}
总结
这类题的核心不是“暴力硬算”，而是“用数学规律简化计算”，结合这道题，我们可以提炼出一套通用思路：
1) 先看暴力，再找痛点
拿到题目先想最直观的暴力解法（比如这题的双重循环枚举所有数对），然后分析它的时间复杂度。
- 当数据规模较大（如 `n ≥ 1e4`）时，`O(n²)` 暴力必然超时，这就是优化的信号。
- 例如本题中 `n ≤ 2×10⁵`，直接暴力会产生 `4×10¹⁰` 次计算，必须换思路。
2) 代数变形：从公式入手
这是最核心的一步，通过数学公式变形，把复杂的累加转化为简单的单次遍历。
- 关键观察：`两两乘积和` 可以用 `(总和)² - 平方和` 间接推导，公式变形后时间复杂度直接降到 `O(n)`。
- 常见变形方向：平方和、立方和、等差数列/等比数列求和、容斥原理等。
3) 时间复杂度预判
根据题目给出的数据范围，反推算法的时间复杂度上限：
- 若 `n ≤ 1e5`，算法时间复杂度最好控制在 `O(n)` 或 `O(n log n)`；
- 若 `n ≤ 1e3`，`O(n²)` 才可能通过。
- 本题中 `n ≤ 2×10⁵`，直接锁定 `O(n)` 级别的解法
4) 数据类型防溢出
计算过程中要注意数值溢出问题：
- 例如本题中，`sum_total` 最大为 `2×10⁵ × 1000 = 2×10⁸`，平方后会达到 `4×10¹⁶`，超出普通 32 位整数范围，需要用 64 位整数（如 Python 的 `int` 天然支持，C++ 中用 `long long`）
关注信息学小助手，获取经济实用的C++入门方案。有想学习C++的，可以在公众号留言，或者联系信息学小助手。
免费加入我的洛谷团队，一起学习、交流、切磋。https://www.luogu.com.cn/team/108017作者简介：华中科技大学本硕，前华为工程师，现高校大数据专业算法课老师。
获得PTA满分认证，可以推荐跨级靠GESP
https://pta.ccf.org.cn/cms/news/100000/0000000114/2025/11/1/514e24a9de984b888ed03803a2fa4434.shtml
