在邹城学信奥赛C++编程之基础算法递推递归案例2

邹城的各位少年你们好,这次我带来的题目是整数划分问题

【题目描述】将正整数n表示成一系列正整数之和:n=n1+n2+...+nk，其中n1≥n2≥...≥nk≥1，k≥1。正整数n的这种表示称为n的划分。n的不同划分个数称为n的划分数，记为p(n)。例如，6有以下11种不同的划分，所以p(6)=11。

6;

5+1;

4+2,4+1+1;

3+3,3+2+1,3+1+1+1;

2+2+2,2+2+1+1,2+1+1+1+1;1+1+1+1+1+1。

输人n，求n的划分数p(2)。

[输入描述】

输人占一行，为一个整数n，1≤n≤400。

【输出描述】

输出占一行，为n的划分数p(n)。

【样例输入1】

120

【样例输出1】

1844349560

【样例输入2】

400

【样例输出2】

6727090051741041926

【分析】

引人记号q(n,m)，表示在正整数n的所有不同划分中，最大加数n1,不超过m(n1≤m)的划分个数。

本题要求的p(n)，实际上就是q(n,n)

分析整数6的11种不同划分的构成，可以得到一个最重要的递推式子:当1     <m<n时，q(n,m)=q(n-m,m)+q(n,m-1)

再补充一些边界情形，就可以建立q(n,m)(n,m均为≥1的整数)的递归关系了。

(1)当=1或m=1时，q(n,m)=1

当最大加数n1不大于m=1时，任何正整数n只有一种划分形式，即n=1+1十...十1。而当n=1时，也只有一种划分形式，即n=1

(2)当m>n时,g(n,m)=q(n,n)

最大加数n1实际上不能大于n，因此当m>n时，q(n,m)=q(n,n)

(3)当n=m时,q(n,m)=q(n,n)=1+q(n,n-1)

正整数n的划分由n1=n的划分(只有1种划分，就是n本身)和n1≤n-1的划分组成

(4)当n>m>1时，q(n,m)=q(n,m-1)+q(n-m,m)

正整数n的最大加数n,不大于m的划分个数q(n,m)，由n,=m的划分个数q(n-m,m)和n,≤m-1的划分个数g(n,m-1)组成。

因此，可以得到下式所示的递推关系。

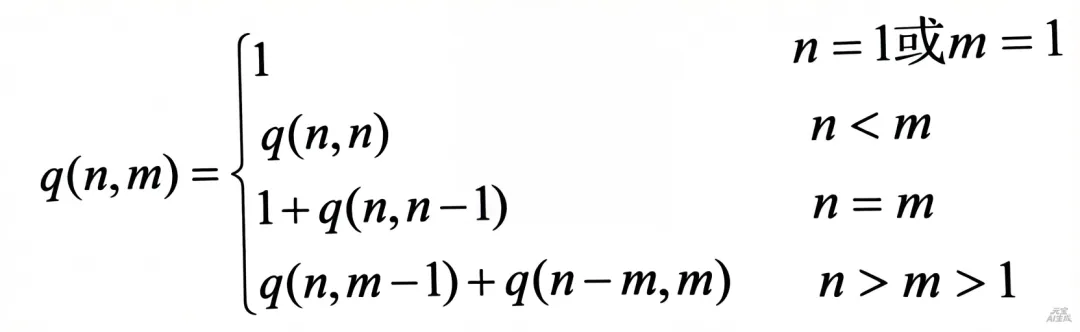
上述递推式子很容易转换成一个递归函数,因而本题目可以使用递归方法求解

但最原始的代码非常容易超时,仅仅需要计算出p(150),在我的电脑上就需要至少6分钟,那如何优化这个代码?

欢迎和我联系沟通交流!