我的Python100天打卡:58/100 第十六章:Numpy数组的规整/一维数组→行列向量/一维数组→二维数组
- 2026-02-05 02:27:44

上次笔记,完成了第十五章的所有部分,并完成了第十五章的三个练习,巩固了Numpy关于数学公式(尤其是一元、二元高斯函数)的表达。今天新开第十六章:Numpy数组的规整。具体内容包括:
16.1 从reshape()函数说起
16.2 一维数组➡️行向量、列向量
16.3 一维数组➡️二维数组
--
先看第十六章的思维导图以及视频讲解:
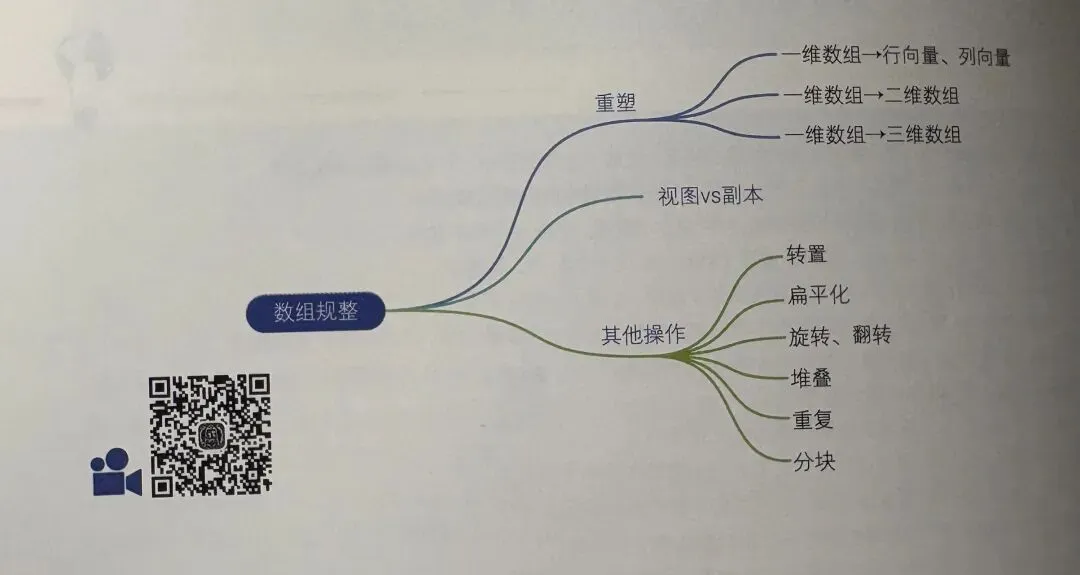
这一章主要关注“数组规整”这部分,包括:
1. “重塑”(包括:一维数组变换为行列向量、变换为二维数组、变换为三维数组)
2. “视图vs副本”(之前有稍微提过)
3. “数组规整的其他操作”(包括:转置、扁平化、旋转翻转、堆叠、重复、分块等)
--
16.1 从reshape()函数说起
在Numpy中,如果要改变数组的形状(也称“重塑数组”),可以使用numpy.reshape()函数。用法如下:
numpy.reshape(a, newshape, order = 'C')这个函数的用法,书本用了一页纸来介绍;我比较懒,还是求助AI助手“百岁太奶”帮我解释下:
1️⃣.reshape() 有什么用:
2️⃣关键参数的解释:

3️⃣一句话解释(含专业术语):





-
16.2 一维数组➡️行向量、列向量
1️⃣需要导入的头文件:
# 导入包import numpy as npimport seaborn as snsimport matplotlib.pyplot as pltimport mathfrom matplotlib import cm# 导入色谱import os# 如果文件夹不存在,创建文件夹if not os.path.isdir("Figures"):os.makedirs("Figures")
2️⃣自定义可视化函数代码:
def visualize_2D(array, title, vmax, vmin):fig_width = math.ceil(array.shape[1] * 0.5)fig_length = math.ceil(array.shape[0] * 0.5)fig, ax = plt.subplots(figsize=(fig_width, fig_length))# 注意,seaborn.heatmap() 目前只能接受2D数组# 本书中,一维数组可视化时用圆圈# 可视化时,只有二维、三维数组用方块sns.heatmap(array,vmax = vmax,vmin = vmin,annot = True, # 增加注释fmt = ".0f", # 注释数值的格式square = True, # 热图方格为正方形cmap = 'RdYlBu_r', # 指定色谱linewidths = .5, # 方格线宽cbar = False, # 不显示色谱条yticklabels=False, # 不显示纵轴标签xticklabels=False, # 不显示横轴标签ax = ax) # 指定绘制热图的轴fig.savefig('Figures/' + title + '.svg', format='svg')# 定义绘制一元数组可视化函数def visualize_1D(array, title):fig, ax = plt.subplots()colors = cm.RdYlBu_r(np.linspace(0,1,len(array)))for idx in range(len(array)):circle_idx = plt.Circle((idx, 0), 0.5, facecolor=colors[idx], edgecolor = 'w')ax.add_patch(circle_idx)ax.text(idx, 0, s = str(array[idx]),horizontalalignment = 'center',verticalalignment = 'center')ax.set_xlim(-0.6, 0.6 + len(array))ax.set_ylim(-0.6, 0.6)ax.set_aspect('equal', adjustable='box')ax.axis('off')fig.savefig('Figures/' + title + '.svg', format='svg')

3️⃣具体执行的变换代码及其运行结果:
2.1 一维数组→行向量
a_row_vector = a_1D_array.reshape(1,-1)# 有时候,当你想要改变数组的形状,但是不确定新的形状应该是多少时,你可以使用 -1 这个特殊值来指定某一个维度的大小np.reshape(a_1D_array, (1,-1))# 把numpy.reshape() 当成一个函数来用np.reshape(a_1D_array, (1,15))# 把numpy.reshape() 当成一个函数来用visualize_2D(a_row_vector, '行向量', 7, -7)

⬆️特别注意:虽然看似只有“一行”,但其实这是一个“行向量”,维度是“二维”的。这个数组的形状为(1,15),也就是行只有一个,列则有15个:

2.2 一维数组→列向量
通过下面的关键代码,使其变为“列向量”(特别注意reshape的第一个参数设置为“-1”):
a_col_vector = a_1D_array.reshape(-1,1)运行可视化结果:

⬆️同样地:虽然看似只有“一列”,但其实这是一个“列向量”,维度是“二维”的。这个数组的形状为(15,1),也就是行有15个,列则有1个。
-
16.3 一维数组➡️二维数组
下面,使用" a = numpy.arange(-7, 7+1)",来生成数组有15个的特定元素的3x5矩阵(二维数组)。

相关实现代码如下:
1️⃣先将之前“重塑”为列向量的数组,重新通过reshape方法,重新转换为二维数组:
A_3_by_5 = a_1D_array.reshape(3, 5)# 先行后列为默认顺序

示例代码提供了【65】和【66】两种排序方法,虽然看起来结果一样,但却是完全不同的排序逻辑:

其中:【65】的参数为(3, -1),意思是先按“一个列必须要排3个元素”来排序,至于能排多少列,由计算机自动计算;
【66】的参数为(-1, 5),意思是按照“每行必须排5人”来算,至于能排多少行,由计算机自动计算。

2️⃣用reshape方法,改为3行5列的矩阵,按照“先列后行”的顺序来排列:
A_3_by_5_col_order = a_1D_array.reshape(3, 5, order = 'F')
3️⃣同样地:5行3列,只需要调换一下reshape方法的参数:
A_5_by_3 = a_1D_array.reshape(5, 3)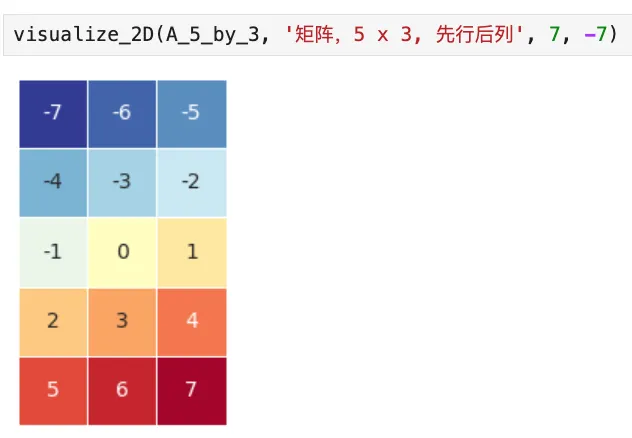
--
时间关系,今天就先写到这里~
今天的笔记也是很快,我的学习重点在于理解参数的位置对于代码的具体影响。
剩下三维数组的变化,明天再继续~
笔记写于:2026年2月4日23:29:05
结束于:2026年2月5日00:17:32
用时:约40分钟
--
