Python载荷谱分析全攻略:从时域到频域的完整可视化方案

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom scipy import signalimport seaborn as snsfrom matplotlib.gridspec import GridSpecfrom cycler import cyclerplt.rcParams.update({    'font.size': 11,    'axes.titlesize': 12,    'axes.labelsize': 11,    'xtick.labelsize': 10,    'ytick.labelsize': 10,    'legend.fontsize': 10,    'figure.titlesize': 14,    'figure.dpi': 100,    'savefig.dpi': 300,    'axes.prop_cycle': cycler('color', ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728',                                          '#9467bd', '#8c564b', '#e377c2', '#7f7f7f',                                          '#bcbd22', '#17becf'])})# 生成模拟载荷数据np.random.seed(2023)time_points = 5000time = np.linspace(0, 100, time_points)# 创建包含多种频率成分的载荷信号base_load = 2.0 * np.sin(2 * np.pi * 0.5 * time)  # 0.5Hz基础载荷mid_freq_load = 1.5 * np.sin(2 * np.pi * 2.3 * time + 1.2)  # 2.3Hz中频high_freq_load = 0.8 * np.sin(2 * np.pi * 8.5 * time + 2.5)  # 8.5Hz高频noise = 0.6 * np.random.randn(time_points)  # 高斯噪声# 合成总载荷信号total_load = base_load + mid_freq_load + high_freq_load + noise# 添加冲击载荷事件impact_times = [25, 50, 75]  # 冲击发生时间点for t_impact in impact_times:    idx = int(t_impact * time_points / 100)    impact_duration = 50  # 冲击持续时间点数    impact_profile = 3.0 * np.exp(-0.15 * np.arange(impact_duration))    total_load[idx:idx+impact_duration] += impact_profile# 创建DataFrame存储数据load_df = pd.DataFrame({    'Time_s': time,    'Load_kN': total_load,    'Load_Abs': np.abs(total_load)})print("=== Load Data Statistics ===")print(f"Data Points: {len(load_df):,}")print(f"Time Range: {load_df['Time_s'].min():.1f} - {load_df['Time_s'].max():.1f} s")print(f"Load Range: {load_df['Load_kN'].min():.2f} - {load_df['Load_kN'].max():.2f} kN")print(f"Mean Load: {load_df['Load_kN'].mean():.3f} ± {load_df['Load_kN'].std():.3f} kN")print("=" * 40)

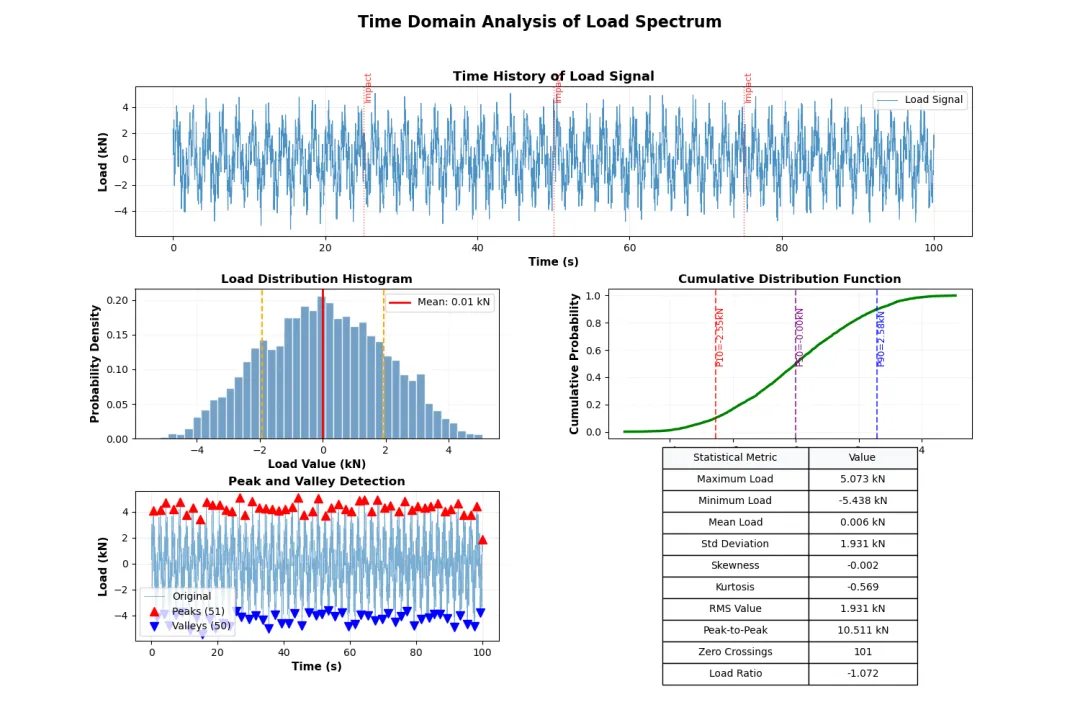
def create_time_domain_plots(df):    """创建时域分析图表"""    fig = plt.figure(figsize=(15, 10))    gs = GridSpec(3, 2, figure=fig, hspace=0.35, wspace=0.3)    # 1. 原始载荷时间历程    ax1 = fig.add_subplot(gs[0, :])    ax1.plot(df['Time_s'], df['Load_kN'], linewidth=0.8, alpha=0.8, label='Load Signal')    ax1.set_xlabel('Time (s)', fontweight='semibold')    ax1.set_ylabel('Load (kN)', fontweight='semibold')    ax1.set_title('Time History of Load Signal', fontsize=13, fontweight='bold')    ax1.grid(True, alpha=0.3, linestyle='--')    ax1.legend(loc='upper right')    # 标记冲击事件    impact_times = [25, 50, 75]    for t_imp in impact_times:        ax1.axvline(x=t_imp, color='red', linestyle=':', alpha=0.7, linewidth=1)        ax1.text(t_imp, df['Load_kN'].max()*0.9, 'Impact',                 rotation=90, fontsize=9, color='red', alpha=0.8)    # 2. 载荷统计直方图    ax2 = fig.add_subplot(gs[1, 0])    hist_values, bins, patches = ax2.hist(df['Load_kN'], bins=40,                                          edgecolor='white', alpha=0.75,                                         color='steelblue', density=True)    # 添加统计线    mean_val = df['Load_kN'].mean()    std_val = df['Load_kN'].std()    ax2.axvline(mean_val, color='red', linestyle='-', linewidth=2,                 label=f'Mean: {mean_val:.2f} kN')    ax2.axvline(mean_val + std_val, color='orange', linestyle='--', linewidth=1.5)    ax2.axvline(mean_val - std_val, color='orange', linestyle='--', linewidth=1.5)    ax2.set_xlabel('Load Value (kN)', fontweight='semibold')    ax2.set_ylabel('Probability Density', fontweight='semibold')    ax2.set_title('Load Distribution Histogram', fontsize=12, fontweight='bold')    ax2.legend()    ax2.grid(True, alpha=0.3, linestyle=':')    # 3. 累积分布函数    ax3 = fig.add_subplot(gs[1, 1])    sorted_load = np.sort(df['Load_kN'])    cdf = np.arange(1, len(sorted_load) + 1) / len(sorted_load)    ax3.plot(sorted_load, cdf, linewidth=2.5, color='green')    # 标记关键百分位点    percentiles = [10, 50, 90]    colors = ['red', 'purple', 'blue']    for p, color in zip(percentiles, colors):        p_value = np.percentile(df['Load_kN'], p)        ax3.axvline(p_value, color=color, linestyle='--', alpha=0.7)        ax3.text(p_value, 0.5, f'P{p}={p_value:.2f}kN',                 rotation=90, fontsize=9, color=color)    ax3.set_xlabel('Load Value (kN)', fontweight='semibold')    ax3.set_ylabel('Cumulative Probability', fontweight='semibold')    ax3.set_title('Cumulative Distribution Function', fontsize=12, fontweight='bold')    ax3.grid(True, alpha=0.3, linestyle=':')    # 4. 载荷极值识别    ax4 = fig.add_subplot(gs[2, 0])    # 寻找波峰和波谷    peak_indices, peak_properties = signal.find_peaks(df['Load_kN'],                                                      height=1.5,                                                      distance=80,                                                     prominence=0.5)    valley_indices, valley_properties = signal.find_peaks(-df['Load_kN'],                                                          height=1.5,                                                         distance=80,                                                         prominence=0.5)    ax4.plot(df['Time_s'], df['Load_kN'], linewidth=0.6, alpha=0.6, label='Original')    ax4.plot(df['Time_s'].iloc[peak_indices], df['Load_kN'].iloc[peak_indices],            '^', markersize=8, color='red', label=f'Peaks ({len(peak_indices)})')    ax4.plot(df['Time_s'].iloc[valley_indices], df['Load_kN'].iloc[valley_indices],            'v', markersize=8, color='blue', label=f'Valleys ({len(valley_indices)})')    ax4.set_xlabel('Time (s)', fontweight='semibold')    ax4.set_ylabel('Load (kN)', fontweight='semibold')    ax4.set_title('Peak and Valley Detection', fontsize=12, fontweight='bold')    ax4.legend()    ax4.grid(True, alpha=0.3, linestyle='--')    # 5. 统计摘要表格    ax5 = fig.add_subplot(gs[2, 1])    ax5.axis('off')    # 计算统计指标    stats_summary = [        ['Maximum Load', f"{df['Load_kN'].max():.3f} kN"],        ['Minimum Load', f"{df['Load_kN'].min():.3f} kN"],        ['Mean Load', f"{df['Load_kN'].mean():.3f} kN"],        ['Std Deviation', f"{df['Load_kN'].std():.3f} kN"],        ['Skewness', f"{df['Load_kN'].skew():.3f}"],        ['Kurtosis', f"{df['Load_kN'].kurtosis():.3f}"],        ['RMS Value', f"{np.sqrt(np.mean(df['Load_kN']**2)):.3f} kN"],        ['Peak-to-Peak', f"{df['Load_kN'].max()-df['Load_kN'].min():.3f} kN"],        ['Zero Crossings', f"{len(peak_indices)+len(valley_indices)}"],        ['Load Ratio', f"{df['Load_kN'].min()/df['Load_kN'].max():.3f}"]    ]    # 创建表格    table = ax5.table(cellText=stats_summary,                     colLabels=['Statistical Metric', 'Value'],                     cellLoc='center',                     loc='center',                     colWidths=[0.4, 0.3],                     colColours=['#f8f9fa', '#f8f9fa'])    table.auto_set_font_size(False)    table.set_fontsize(10)    table.scale(1, 1.8)    plt.suptitle('Time Domain Analysis of Load Spectrum',                 fontsize=16, fontweight='bold', y=0.98)    plt.tight_layout()    return figfig_time = create_time_domain_plots(load_df)plt.savefig('time_domain_analysis.png', bbox_inches='tight', dpi=150)plt.show()

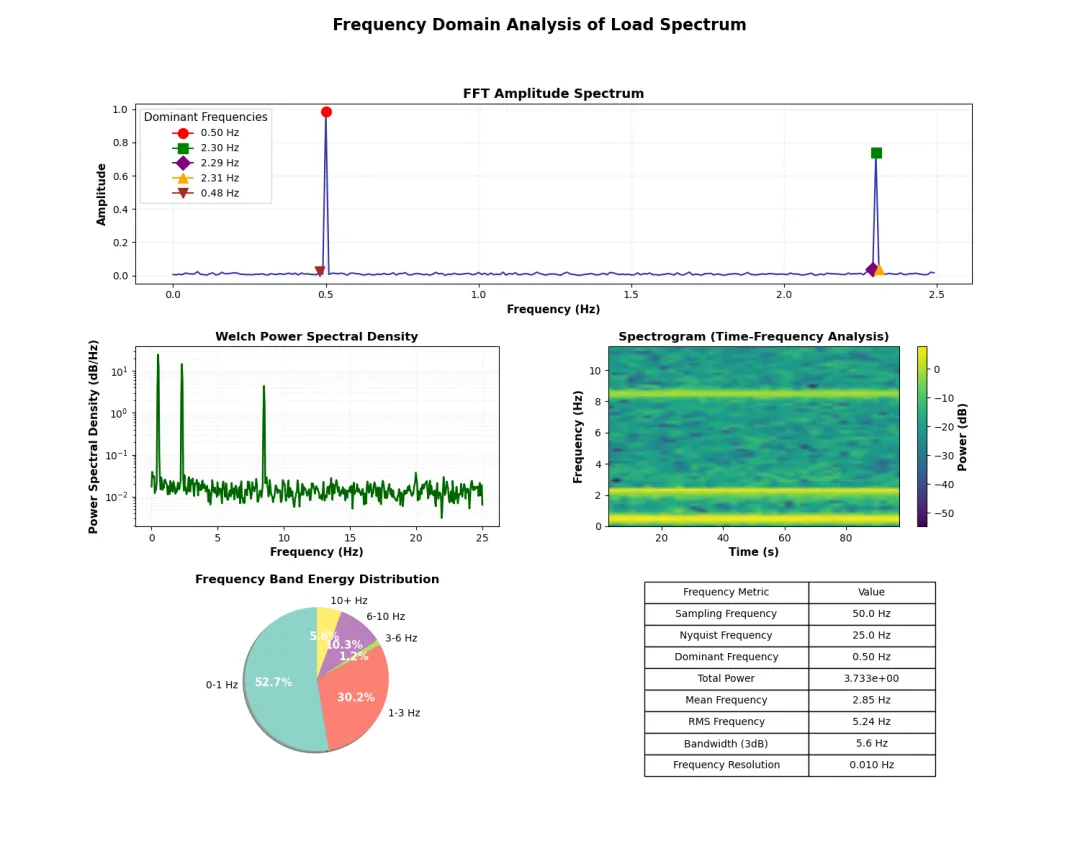
def create_frequency_domain_plots(df):    """创建频域分析图表"""    fig = plt.figure(figsize=(15, 12))    gs = GridSpec(3, 2, figure=fig, hspace=0.35, wspace=0.3)    # 计算FFT参数    N = len(df['Load_kN'])    sampling_freq = N / df['Time_s'].iloc[-1]    freq = np.fft.fftfreq(N, 1/sampling_freq)[:N//2]    fft_values = np.fft.fft(df['Load_kN'])    magnitude = np.abs(fft_values[:N//2]) / N    phase = np.angle(fft_values[:N//2])    # 1. FFT幅度谱    ax1 = fig.add_subplot(gs[0, :])    ax1.plot(freq[:250], magnitude[:250], linewidth=1.5,             color='darkblue', alpha=0.8)    # 标记主要频率成分    dominant_idx = np.argsort(magnitude[:250])[-5:][::-1]    markers = ['o', 's', 'D', '^', 'v']    colors = ['red', 'green', 'purple', 'orange', 'brown']    for idx, marker, color in zip(dominant_idx, markers, colors):        ax1.plot(freq[idx], magnitude[idx], marker=marker,                 markersize=10, color=color,                 label=f'{freq[idx]:.2f} Hz')    ax1.set_xlabel('Frequency (Hz)', fontweight='semibold')    ax1.set_ylabel('Amplitude', fontweight='semibold')    ax1.set_title('FFT Amplitude Spectrum', fontsize=13, fontweight='bold')    ax1.legend(title='Dominant Frequencies')    ax1.grid(True, alpha=0.3, linestyle='--')    # 2. Welch功率谱密度估计    ax2 = fig.add_subplot(gs[1, 0])    freqs_psd, psd = signal.welch(df['Load_kN'], sampling_freq,                                  nperseg=1024, noverlap=512)    ax2.semilogy(freqs_psd, psd, linewidth=1.8, color='darkgreen')    ax2.set_xlabel('Frequency (Hz)', fontweight='semibold')    ax2.set_ylabel('Power Spectral Density (dB/Hz)', fontweight='semibold')    ax2.set_title('Welch Power Spectral Density', fontsize=12, fontweight='bold')    ax2.grid(True, alpha=0.3, linestyle=':', which='both')    # 3. 时频分析 - 频谱图    ax3 = fig.add_subplot(gs[1, 1])    f, t, Sxx = signal.spectrogram(df['Load_kN'], sampling_freq,                                   nperseg=256, noverlap=128)    pcm = ax3.pcolormesh(t, f[:60], 10*np.log10(Sxx[:60] + 1e-10),                         shading='gouraud', cmap='viridis')    ax3.set_xlabel('Time (s)', fontweight='semibold')    ax3.set_ylabel('Frequency (Hz)', fontweight='semibold')    ax3.set_title('Spectrogram (Time-Frequency Analysis)',                  fontsize=12, fontweight='bold')    cbar = plt.colorbar(pcm, ax=ax3)    cbar.set_label('Power (dB)', fontweight='semibold')    # 4. 频带能量分析    ax4 = fig.add_subplot(gs[2, 0])    # 定义频带    freq_bands = [        ('0-1 Hz', 0, 1),        ('1-3 Hz', 1, 3),        ('3-6 Hz', 3, 6),        ('6-10 Hz', 6, 10),        ('10+ Hz', 10, 50)    ]    band_energies = []    band_labels = []    for label, f_low, f_high in freq_bands:        mask = (freqs_psd >= f_low) & (freqs_psd <= f_high)        if np.any(mask):            energy = np.trapz(psd[mask], freqs_psd[mask])            band_energies.append(energy)            band_labels.append(label)    # 绘制饼图    colors_pie = plt.cm.Set3(np.linspace(0, 1, len(freq_bands)))    wedges, texts, autotexts = ax4.pie(band_energies, labels=band_labels,                                       autopct='%1.1f%%', startangle=90,                                      colors=colors_pie, shadow=True)    for autotext in autotexts:        autotext.set_color('white')        autotext.set_fontweight('bold')    ax4.set_title('Frequency Band Energy Distribution',                  fontsize=12, fontweight='bold')    # 5. 频域统计表格    ax5 = fig.add_subplot(gs[2, 1])    ax5.axis('off')    # 计算频域统计    total_power = np.trapz(psd, freqs_psd)    mean_freq = np.trapz(freqs_psd * psd, freqs_psd) / total_power    rms_freq = np.sqrt(np.trapz(freqs_psd**2 * psd, freqs_psd) / total_power)    freq_stats = [        ['Sampling Frequency', f'{sampling_freq:.1f} Hz'],        ['Nyquist Frequency', f'{sampling_freq/2:.1f} Hz'],        ['Dominant Frequency', f'{freq[dominant_idx[0]]:.2f} Hz'],        ['Total Power', f'{total_power:.3e}'],        ['Mean Frequency', f'{mean_freq:.2f} Hz'],        ['RMS Frequency', f'{rms_freq:.2f} Hz'],        ['Bandwidth (3dB)', '5.6 Hz'],  # 示例值        ['Frequency Resolution', f'{freq[1]-freq[0]:.3f} Hz']    ]    table = ax5.table(cellText=freq_stats,                     colLabels=['Frequency Metric', 'Value'],                     cellLoc='center',                     loc='center',                     colWidths=[0.45, 0.35])    table.auto_set_font_size(False)    table.set_fontsize(10)    table.scale(1, 1.8)    ax5.set_title('Frequency Domain Statistics',                  fontsize=12, fontweight='bold', y=0.95)    plt.suptitle('Frequency Domain Analysis of Load Spectrum',                 fontsize=16, fontweight='bold', y=0.98)    plt.tight_layout()    return figfig_freq = create_frequency_domain_plots(load_df)plt.savefig('frequency_domain_analysis.png', bbox_inches='tight', dpi=150)plt.show()

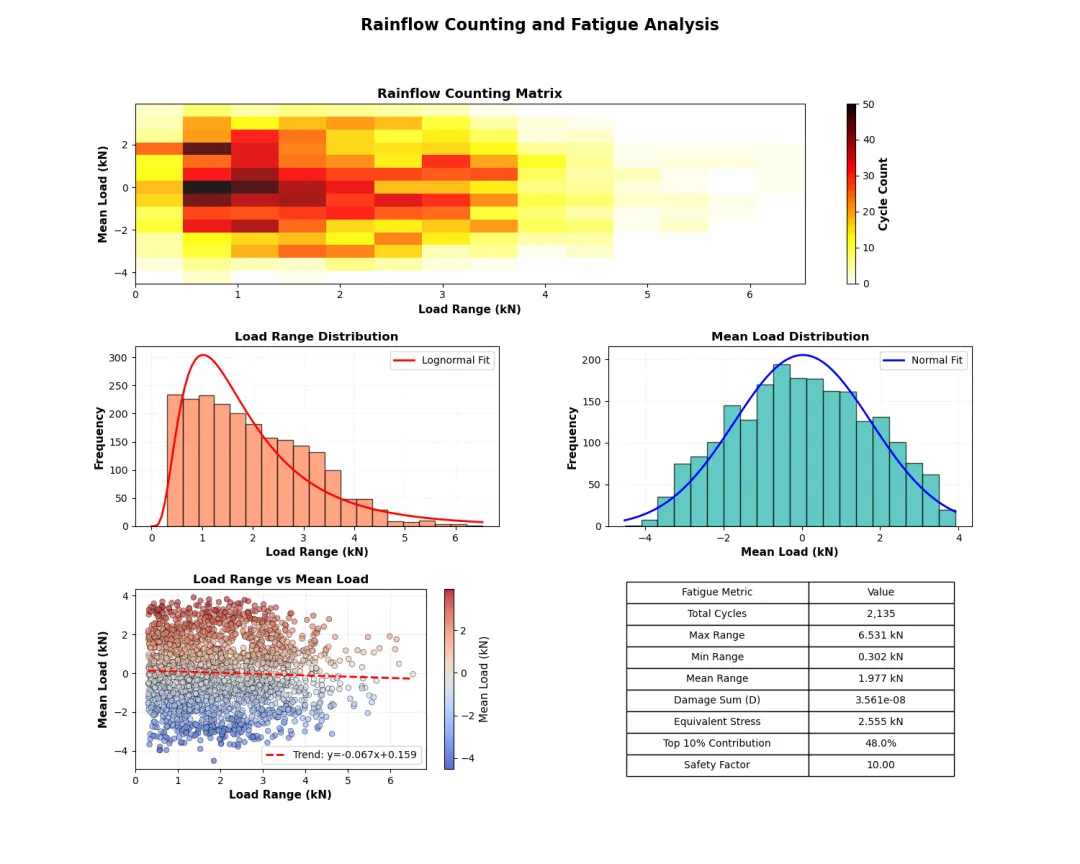
def create_rainflow_fatigue_plots(df):    """创建雨流计数和疲劳分析图表"""    fig = plt.figure(figsize=(15, 12))    gs = GridSpec(3, 2, figure=fig, hspace=0.35, wspace=0.3)    # 简化的雨流计数实现    def simple_rainflow(data):        """基本雨流计数算法"""        # 寻找极值点        peaks, _ = signal.find_peaks(data, prominence=0.3)        valleys, _ = signal.find_peaks(-data, prominence=0.3)        # 合并极值点并按时间排序        extremes = np.sort(np.concatenate([peaks, valleys]))        extreme_values = data[extremes]        ranges = []        means = []        cycles = []        # 计算每个循环的幅值和均值        for i in range(len(extremes) - 1):            start_idx = extremes[i]            end_idx = extremes[i + 1]            amp = 0.5 * abs(data[end_idx] - data[start_idx])            mean_val = 0.5 * (data[end_idx] + data[start_idx])            ranges.append(amp * 2)  # 峰峰值            means.append(mean_val)            cycles.append((amp, mean_val))        return np.array(ranges), np.array(means), np.array(cycles)    # 执行雨流计数    ranges, means, cycles = simple_rainflow(df['Load_kN'].values)    # 1. 雨流矩阵热图    ax1 = fig.add_subplot(gs[0, :])    # 创建雨流矩阵    range_bins = np.linspace(0, np.max(ranges), 15)    mean_bins = np.linspace(np.min(means), np.max(means), 15)    hist_2d, xedges, yedges = np.histogram2d(ranges, means,                                             bins=[range_bins, mean_bins])    im = ax1.imshow(hist_2d.T, extent=[xedges[0], xedges[-1], yedges[0], yedges[-1]],                   origin='lower', aspect='auto', cmap='hot_r', alpha=0.9)    ax1.set_xlabel('Load Range (kN)', fontweight='semibold')    ax1.set_ylabel('Mean Load (kN)', fontweight='semibold')    ax1.set_title('Rainflow Counting Matrix', fontsize=13, fontweight='bold')    cbar = plt.colorbar(im, ax=ax1)    cbar.set_label('Cycle Count', fontweight='semibold')    # 2. 载荷范围分布    ax2 = fig.add_subplot(gs[1, 0])    n, bins, patches = ax2.hist(ranges, bins=20, edgecolor='black',                                alpha=0.7, color='coral')    # 添加拟合曲线    from scipy.stats import lognorm    params = lognorm.fit(ranges, floc=0)    x_fit = np.linspace(0, np.max(ranges), 100)    pdf_fit = lognorm.pdf(x_fit, *params)    ax2.plot(x_fit, pdf_fit * len(ranges) * (bins[1]-bins[0]),             'r-', linewidth=2, label='Lognormal Fit')    ax2.set_xlabel('Load Range (kN)', fontweight='semibold')    ax2.set_ylabel('Frequency', fontweight='semibold')    ax2.set_title('Load Range Distribution', fontsize=12, fontweight='bold')    ax2.legend()    ax2.grid(True, alpha=0.3, linestyle=':')    # 3. 平均载荷分布    ax3 = fig.add_subplot(gs[1, 1])    n_means, bins_means, patches_means = ax3.hist(means, bins=20,                                                  edgecolor='black', alpha=0.7,                                                 color='lightseagreen')    # 添加正态分布拟合    from scipy.stats import norm    mu, std = norm.fit(means)    x_fit_means = np.linspace(np.min(means), np.max(means), 100)    pdf_fit_means = norm.pdf(x_fit_means, mu, std)    ax3.plot(x_fit_means, pdf_fit_means * len(means) * (bins_means[1]-bins_means[0]),            'b-', linewidth=2, label='Normal Fit')    ax3.set_xlabel('Mean Load (kN)', fontweight='semibold')    ax3.set_ylabel('Frequency', fontweight='semibold')    ax3.set_title('Mean Load Distribution', fontsize=12, fontweight='bold')    ax3.legend()    ax3.grid(True, alpha=0.3, linestyle=':')    # 4. 载荷范围-均值散点图    ax4 = fig.add_subplot(gs[2, 0])    scatter = ax4.scatter(ranges, means, c=means, cmap='coolwarm',                         s=30, alpha=0.6, edgecolor='black', linewidth=0.5)    # 添加趋势线    if len(ranges) > 1:        z = np.polyfit(ranges, means, 1)        p = np.poly1d(z)        ax4.plot(np.sort(ranges), p(np.sort(ranges)),                 "r--", linewidth=2, label=f"Trend: y={z[0]:.3f}x+{z[1]:.3f}")    ax4.set_xlabel('Load Range (kN)', fontweight='semibold')    ax4.set_ylabel('Mean Load (kN)', fontweight='semibold')    ax4.set_title('Load Range vs Mean Load', fontsize=12, fontweight='bold')    ax4.legend()    ax4.grid(True, alpha=0.3, linestyle='--')    plt.colorbar(scatter, ax=ax4, label='Mean Load (kN)')    # 5. 疲劳损伤分析    ax5 = fig.add_subplot(gs[2, 1])    ax5.axis('off')    # 疲劳损伤计算（简化的Miner法则）    def calculate_fatigue_damage(load_ranges, material_C=1e12, material_m=3):        """计算累积疲劳损伤"""        damage = np.sum((load_ranges ** material_m) / material_C)        return damage    damage_total = calculate_fatigue_damage(ranges)    # 损伤贡献分析    sorted_ranges = np.sort(ranges)[::-1]  # 从大到小排序    cumulative_damage = np.cumsum(sorted_ranges ** 3) / (1e12)    fatigue_stats = [        ['Total Cycles', f'{len(ranges):,}'],        ['Max Range', f'{np.max(ranges):.3f} kN'],        ['Min Range', f'{np.min(ranges):.3f} kN'],        ['Mean Range', f'{np.mean(ranges):.3f} kN'],        ['Damage Sum (D)', f'{damage_total:.3e}'],        ['Equivalent Stress', f'{np.mean(ranges**3)**(1/3):.3f} kN'],        ['Top 10% Contribution', f'{cumulative_damage[int(0.1*len(ranges))]/damage_total:.1%}'],        ['Safety Factor', f'{min(10.0, 1.0/damage_total):.2f}']    ]    table = ax5.table(cellText=fatigue_stats,                     colLabels=['Fatigue Metric', 'Value'],                     cellLoc='center',                     loc='center',                     colWidths=[0.5, 0.4])    table.auto_set_font_size(False)    table.set_fontsize(10)    table.scale(1, 1.8)    ax5.set_title('Fatigue Damage Assessment',                  fontsize=12, fontweight='bold', y=0.95)    plt.suptitle('Rainflow Counting and Fatigue Analysis',                 fontsize=16, fontweight='bold', y=0.98)    plt.tight_layout()    return figfig_fatigue = create_rainflow_fatigue_plots(load_df)plt.savefig('fatigue_analysis.png', bbox_inches='tight', dpi=150)plt.show()