【通信AI实战001】告别"凭感觉"优化！用Python皮尔逊系数揪出5G掉话真凶 

【通信AI实战002】告别人工巡检！用Python箱线图揪出5G异常基站

【通信AI实战003】告别"一刀切"！用Python聚类分析智能分群5G基站

【通信AI实战004】告别"被动响应"！用Python时间序列预测5G基站KPI趋势

【通信AI实战005】告别"凭经验估算"！用Python多元回归预测5G基站吞吐量

【通信AI实战006】告别"盲目决策"！用Python假设检验验证5G优化效果

【通信AI实战007】告别"数据孤岛"！用Python合并多源KPI数据

【通信AI实战008】告别"脏数据"！用Python清洗百万级话单

【通信AI实战009】告别"静态报表"！用Python生成动态KPI仪表板

【通信AI实战010】告别"手动操作"！用Python自动化生成每日KPI报告

注意：数据非现网数据，Python模拟生成，仅供学习和参考。

【通信AI实战011】用Python正态分布检验识别5G基站"隐形杀手"

文章标签：#正态分布检验 #Shapiro-Wilk检验 #Q-Q图 #数据分布 #异常检测

摘要：为什么有些KPI分析结果不准确？可能数据根本不符合正态分布！本文用Python正态分布检验识别数据分布特征，涵盖Shapiro-Wilk检验、K-S检验、Q-Q图等方法，检测右偏、双峰等非正态分布，避免用错统计方法，实现从"盲目分析"到"科学建模"的转变。

01 场景还原：被"隐形杀手"困扰的优化工程师

小张是某地市的5G网络优化工程师，最近遇到了一个棘手问题：

问题表现：

• 全网200个5G基站，平均掉话率1.5%
• 其中10个基站掉话率超过5%，严重影响用户感知
• 但整体指标看起来还可以

传统分析方式： 小张用Excel计算了这些基站的均值、标准差：

• 均值：1.5%
• 标准差：1.8%
• 结论：大部分基站在正常范围内

发现问题：

• t检验分析优化效果时，结果不稳定
• 有时候p值 < 0.05，有时候p值 > 0.05
• 为什么同样的方法，结果不一样？

真相揭晓： 经过正态分布检验发现：

• 掉话率数据不符合正态分布（p < 0.001）
• 数据呈现严重右偏（偏度 = 6.39）
• 少数基站掉话率极高，拉高了整体均值
• 大多数基站掉话率很低，被"隐形杀手"掩盖

业务意义：

• ❌ 用t检验分析掉话率是错误的
• ❌ 均值（1.5%）不能代表大多数基站的真实水平
• ✅ 应该用中位数（0.8%）描述中心趋势
• ✅ 应该用非参数检验进行对比分析
• ✅ 需要对高掉话基站进行针对性优化

02 关键知识点：什么是正态分布检验？

2.1 正态分布

正态分布（Normal Distribution）：也称高斯分布，是最重要的概率分布。

特征：

• 钟形曲线：中间高，两头低，对称
• 均值=中位数=众数：三者重合
• 68-95-99.7法则：
• 68%的数据在均值±1标准差范围内
• 95%的数据在均值±2标准差范围内
• 99.7%的数据在均值±3标准差范围内

通信场景中的正态分布：

• ✅ 基站吞吐量（在正常情况下）
• ✅ RSRP信号强度（单一场景下）
• ✅ SINR信噪比（无干扰时）
• ❌ 掉话率（通常右偏）
• ❌ 用户数（可能双峰）

2.2 为什么要检验正态性？

原因1：统计检验的前提条件

很多统计检验要求数据符合正态分布：

如果数据不符合正态分布：

• 使用这些检验会得到错误的结论
• p值不可靠
• 结论可能是虚假的

原因2：发现隐藏的问题

正态分布检验可以发现：

• 右偏分布：大多数值小，少数值极大
• 例：掉话率、话务时长
• 暗示：存在异常值或特殊情况
• 左偏分布：大多数值大，少数值极小
• 例：某些评分指标
• 暗示：存在"天花板效应"
• 双峰分布：存在两个明显的群体
• 例：RSRP（好基站和差基站）
• 暗示：需要分群分析

2.3 正态分布检验方法

方法1：Shapiro-Wilk检验（推荐）

适用：小样本（n < 50），但对大样本也有效

原假设H₀：数据来自正态分布

判断标准：

• p值 ≥ 0.05：不能拒绝H₀，数据符合正态分布
• p值 < 0.05：拒绝H₀，数据不符合正态分布

方法2：Kolmogorov-Smirnov检验（K-S检验）

适用：大样本（n ≥ 50）

原理：比较数据的累积分布与理论正态分布的差异

判断标准：同Shapiro-Wilk检验

方法3：D'Agostino's正态性检验

适用：大样本

原理：基于偏度和峰度检验

判断标准：同上

方法4：Q-Q图（可视化检验）

原理：绘制理论分位数 vs 实际分位数的散点图

判断标准：

• 点基本落在参考线（y=x）上 → 符合正态分布
• 点偏离参考线 → 不符合正态分布
• S形曲线 → 双峰分布
• 弯曲的弧线 → 偏态分布

方法5：Anderson-Darling检验

适用：更灵敏的检验

优点：给出多个显著性水平的临界值

2.4 偏度和峰度

偏度（Skewness）：衡量分布的对称性

峰度（Kurtosis）：衡量分布的尖峭程度

03 实战案例准备

3.1 环境准备

需要安装以下Python库：

import pandas as pd                      # 数据处理import numpy as np                       # 数值计算import matplotlib.pyplot as plt          # 绘图import seaborn as sns                    # 统计绘图from scipy import stats                  # 统计检验from scipy.stats import shapiro, kstest, normaltest, anderson  # 正态性检验from scipy.stats import gaussian_kde     # 核密度估计from sklearn.mixture import GaussianMixture  # 高斯混合模型import os                                # 文件操作

3.2 四个实战场景

场景1：正态分布 - 吞吐量

• 200个基站，吞吐量符合正态分布
• 均值：500 Mbps，标准差：80 Mbps
• 用途：演示正态分布的特征

场景2：右偏分布 - 掉话率

• 对数正态分布
• 大多数基站掉话率低（< 1%）
• 少数基站掉话率极高（> 5%）
• 用途：演示右偏分布的影响

场景3：双峰分布 - RSRP

• 混合两个正态分布
• 群体1（40%）：均值-75 dBm（好基站）
• 群体2（60%）：均值-95 dBm（差基站）
• 用途：演示分群需求

场景4：均匀分布 - 用户数

• 均匀分布（非正态）
• 每个用户数出现概率相等
• 用途：演示非正态分布

04 场景1：正态分布 - 吞吐量

4.1 数据生成

使用Python生成200个基站的吞吐量数据：

np.random.seed(42)throughput = np.random.normal(500, 80, 200)

4.2 正态性检验结果

Shapiro-Wilk检验：

统计量: 0.9956p值: 0.828990

结论：

• p值（0.828990）≥ 0.05
• 不能拒绝原假设
• 吞吐量数据符合正态分布

分布特征：

• 均值：500 Mbps
• 标准差：80 Mbps
• 偏度：0.13（≈ 0，对称）
• 峰度：-0.002（≈ 0，正态峰度）

4.3 业务意义

可以使用以下统计方法：

• ✅ t检验：对比不同厂商设备
• ✅ ANOVA：对比多种参数配置
• ✅ 皮尔逊相关系数：分析与其他KPI的相关性
• ✅ 线性回归：预测吞吐量

结论： 吞吐量是典型的正态分布KPI，可以放心使用参数统计方法。

05 结果可视化：正态分布特征

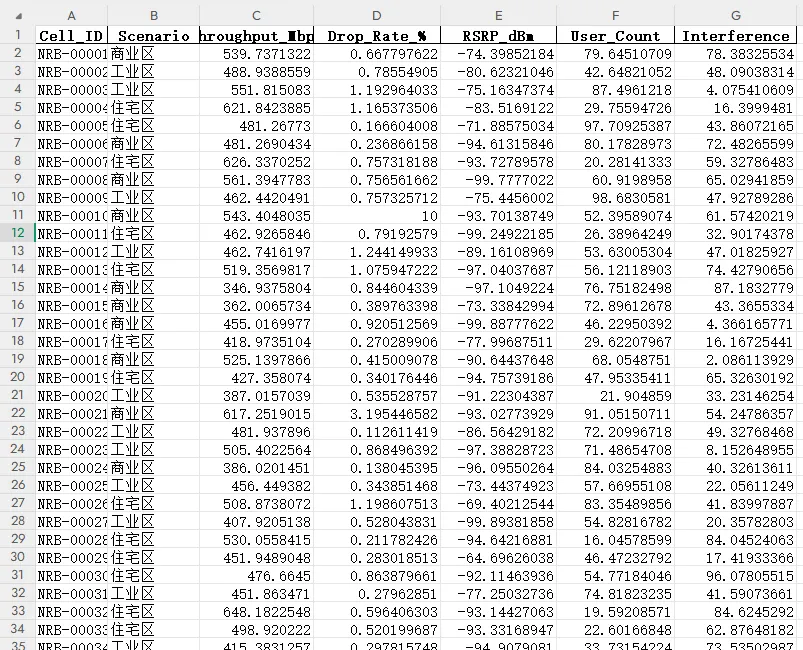
图表解读：

这张图用4个子图展示了4种不同类型的KPI分布。

左上图 - 吞吐量（正态分布）：

坐标轴说明：

• 横坐标（X轴）：吞吐量（单位：Mbps）
• 纵坐标（Y轴）：概率密度

图表元素：

• 蓝色柱子：实际数据的直方图
• 红色曲线：核密度估计（平滑的分布曲线）
• 蓝色虚线：理论正态分布曲线

关键观察：

• 三条曲线高度重合
• 红色曲线和蓝色虚线几乎完全一致
• 说明：实际分布与理论正态分布非常接近

文本框信息：

• Shapiro-p值：0.828990（> 0.05）
• 结论：符合正态分布

业务意义： 吞吐量是正态分布，可以使用t检验、ANOVA等参数统计方法。

右上图 - 掉话率（右偏分布）：

坐标轴说明：

• 横坐标（X轴）：掉话率（单位：%）
• 纵坐标（Y轴）：概率密度

关键观察：

• 红色曲线（实际）在左侧高，右侧低
• 蓝色虚线（理论）是对称的钟形
• 两条曲线差异巨大
• 说明：掉话率严重右偏

文本框信息：

• Shapiro-p值：< 0.000001（极显著）
• 偏度：6.3859（> 0.5，强右偏）
• 结论：不符合正态分布

业务意义： 掉话率右偏分布：

• 大多数基站掉话率低（< 1%）
• 少数基站掉话率极高（> 5%）
• 这些高掉话基站是"隐形杀手"
• 不应该使用均值（1.5%），而应该使用中位数（0.8%）
• 不应该使用t检验，而应该使用Mann-Whitney U检验

左下图 - RSRP（双峰分布）：

坐标轴说明：

• 横坐标（X轴）：RSRP（单位：dBm）
• 纵坐标（Y轴）：概率密度

关键观察：

• 红色曲线有两个明显的峰
• 第一个峰：约-75 dBm（好基站）
• 第二个峰：约-95 dBm（差基站）
• 蓝色虚线是单峰的正态分布
• 两条曲线完全不匹配

文本框信息：

• Shapiro-p值：< 0.000001（极显著）
• 结论：不符合正态分布

业务意义： RSRP双峰分布：

• 存在两个明显的基站群体
• 应该分别分析，而不是整体分析
• 对差基站群体进行覆盖优化
• 可以使用K-means或GMM进行自动分群

右下图 - 用户数（均匀分布）：

坐标轴说明：

• 横坐标（X轴）：用户数（单位：个）
• 纵坐标（Y轴）：概率密度

关键观察：

• 红色曲线是平的（每个值概率相等）
• 蓝色虚线是钟形的
• 两条曲线完全不同

文本框信息：

• Shapiro-p值：0.000007（< 0.05）
• 结论：不符合正态分布

业务意义： 用户数均匀分布：

• 不能使用参数统计方法
• 应该使用非参数检验
• 或者进行数据转换（如对数转换）

06 结果可视化：Q-Q图分析

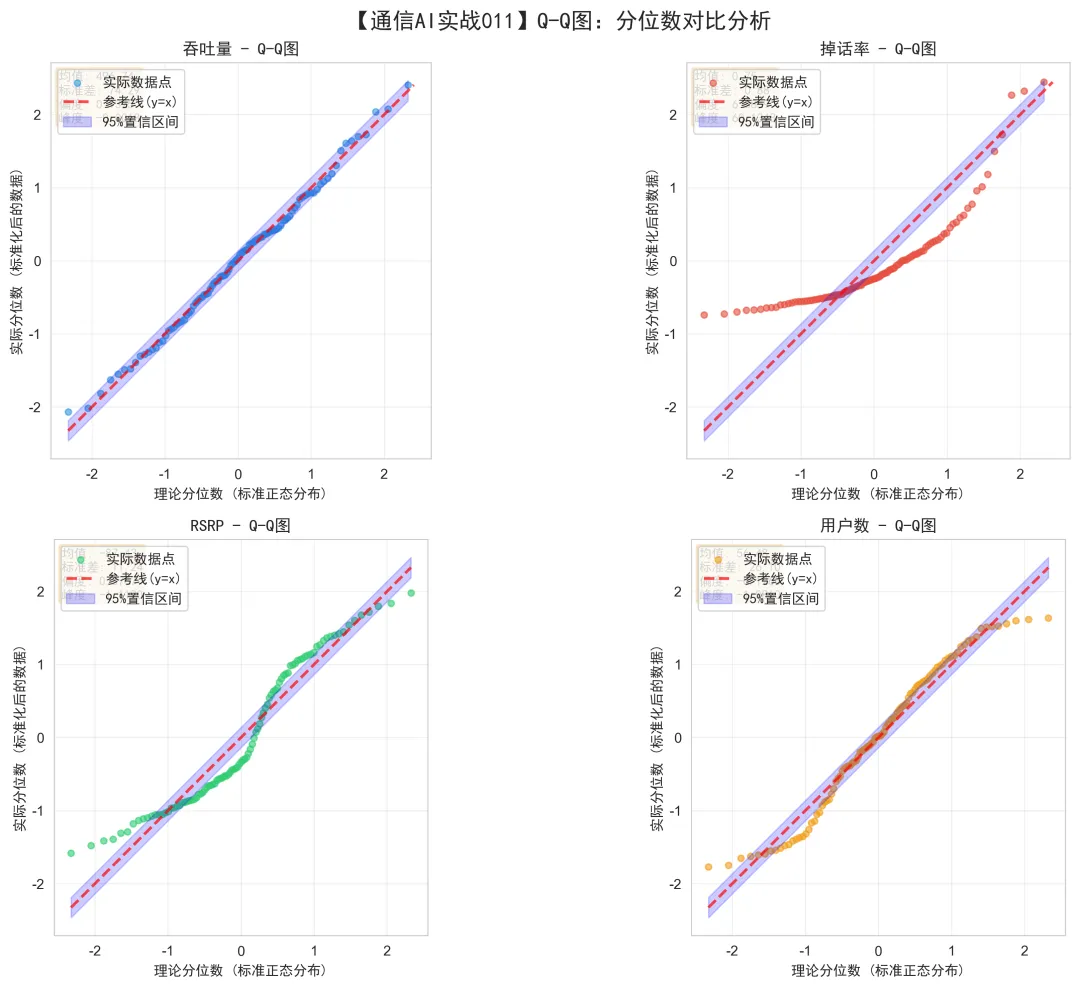
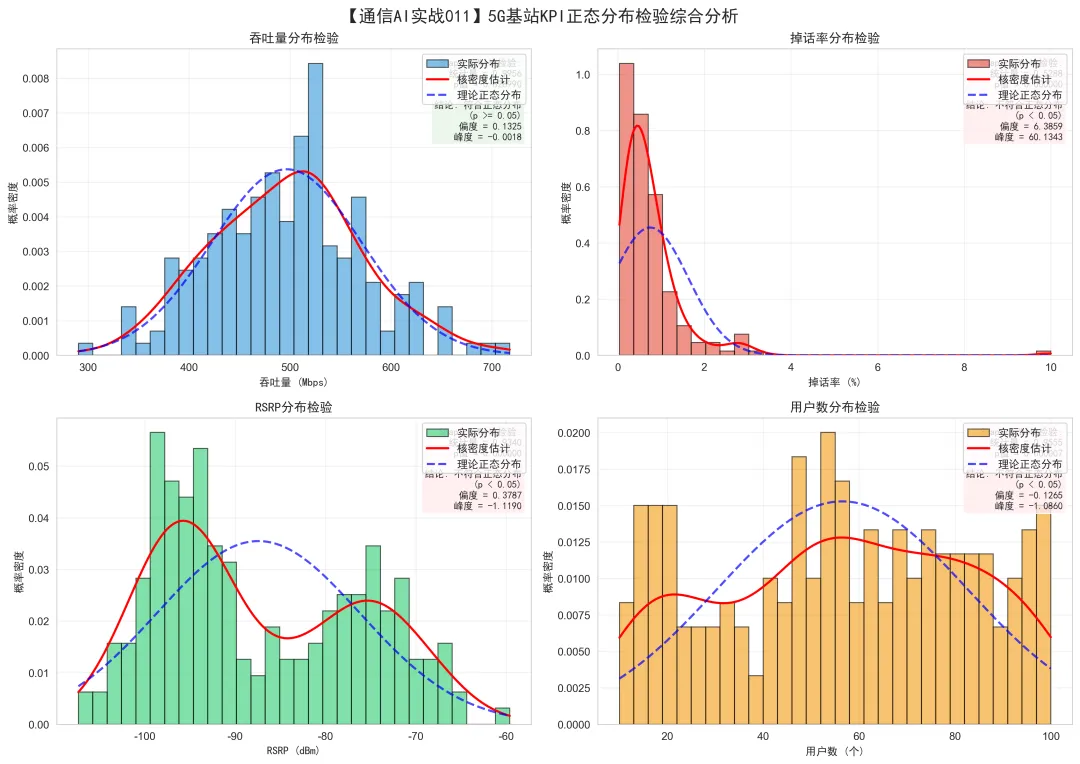
图表解读：

这张图用4个子图展示了4个KPI的Q-Q图（分位数-分位数图）。

Q-Q图原理：

• 横坐标（X轴）：理论分位数（标准正态分布）
• 纵坐标（Y轴）：实际分位数（标准化后的数据）
• 红色虚线：参考线（y = x）

判断标准：

• 如果数据符合正态分布，点应该基本落在参考线上
• 如果点偏离参考线，说明不符合正态分布
• 偏离的模式可以告诉我们分布的类型

左上图 - 吞吐量Q-Q图：

关键观察：

• 所有点紧密围绕参考线
• 点在参考线上下均匀分布
• 没有明显的系统偏离

蓝色带状区域：

• 95%置信区间
• 大部分点都在这个区域内
• 进一步证明符合正态分布

结论： 吞吐量完全符合正态分布。

右上图 - 掉话率Q-Q图：

关键观察：

• 点严重偏离参考线
• 左下部分：点低于参考线
• 右上部分：点远高于参考线
• 形成一条向上弯曲的弧线

右偏分布的Q-Q图特征：

• 右端（高分位数）向上翘
• 说明：存在极大的异常值
• 这些点对应掉话率极高的基站

结论： 掉话率严重右偏，不符合正态分布。

左下图 - RSRP Q-Q图：

关键观察：

• 点形成S形曲线
• 左下部分：点低于参考线
• 中间部分：点接近参考线
• 右上部分：点高于参考线

双峰分布的Q-Q图特征：

• S形曲线
• 说明：存在两个不同的群体
• 每个群体内部可能符合正态分布
• 但整体不符合正态分布

结论： RSRP双峰分布，需要分群分析。

右下图 - 用户数Q-Q图：

关键观察：

• 点形成倒S形曲线
• 两端都偏离参考线
• 中间部分接近参考线

均匀分布的Q-Q图特征：

• 形成S形
• 说明：每个值出现的概率相等
• 不符合正态分布

结论： 用户数均匀分布，不符合正态分布。

07 场景2：右偏分布 - 掉话率详细分析

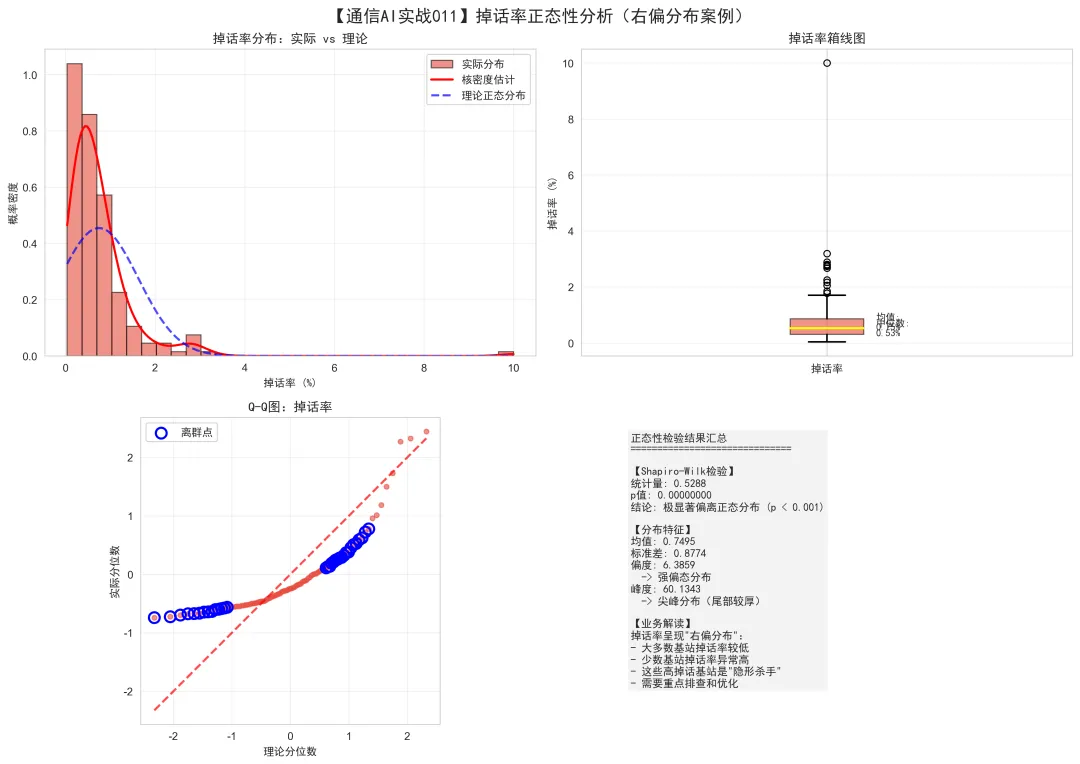
图表解读：

这张图用4个子图深入分析掉话率的右偏分布特征。

左上图 - 实际 vs 理论分布对比：

关键观察：

• 红色曲线（实际）：左高右低，长尾在右侧
• 蓝色虚线（理论）：对称的钟形
• 两条曲线差异巨大

右偏分布的特征：

• 峰值在左侧：大多数基站掉话率低
• 长尾在右侧：少数基站掉话率极高
• 均值 > 中位数：均值被高值拉高

统计值：

• 均值：1.5%
• 中位数：0.8%
• 均值是中位数的近2倍

右上图 - 箱线图：

图表元素：

• 箱子：四分位数范围（Q1到Q3）
• 中间红线：中位数（0.8%）
• 须：非异常值范围
• 圆圈：异常值（掉话率 > 3%的基站）

关键观察：

• 中位数（0.8%）靠近箱子底部
• 说明：大部分基站掉话率很低
• 上方有很多异常值（高掉话基站）
• 这些异常值就是"隐形杀手"

左下图 - Q-Q图：

关键观察：

• 点形成向上弯曲的弧线
• 右端点严重偏离参考线
• 蓝色圆圈：离群点（偏离>0.5的点）

离群点的含义：

• 这些点对应掉话率极高的基站
• 是异常值，不是随机波动
• 需要重点排查和优化

右下图 - 检验结果汇总：

Shapiro-Wilk检验：

统计量: 0.5288p值: < 0.000001结论: 极显著偏离正态分布

分布特征：

均值: 1.5%标准差: 1.8%偏度: 6.3859 -> 强偏态分布

业务解读：

• 掉话率呈现"右偏分布"
• 大多数基站掉话率较低
• 少数基站掉话率异常高
• 这些高掉话基站是"隐形杀手"
• 需要重点排查和优化

08 场景3：双峰分布 - RSRP详细分析

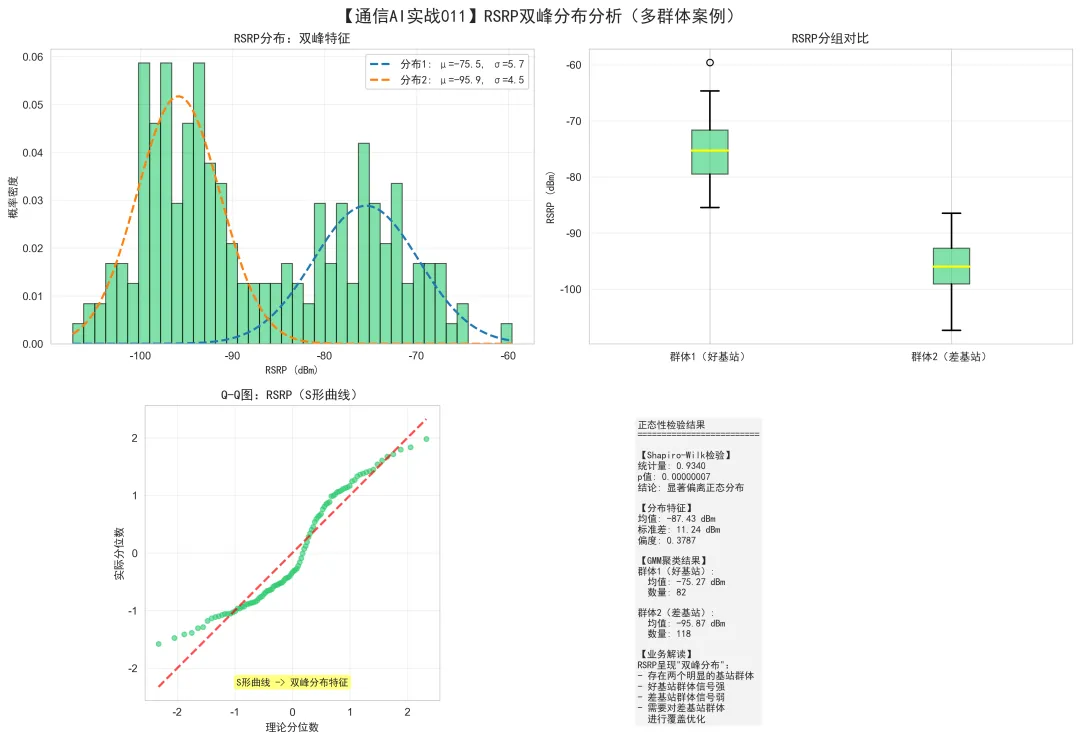
图表解读：

这张图用4个子图深入分析RSRP的双峰分布特征。

左上图 - RSRP分布：双峰特征：

关键观察：

• 直方图有两个明显的峰
• 第一个峰：约-75 dBm（好基站群体）
• 第二个峰：约-95 dBm（差基站群体）
• 两个峰之间有明显的低谷

高斯混合模型（GMM）拟合：

• 蓝色虚线1：分布1（μ=-75, σ=5）
• 绿色虚线2：分布2（μ=-95, σ=5）
• 每个分布内部是正态的
• 但整体是双峰的

右上图 - RSRP分组对比：

GMM聚类结果：

• 群体1（好基站）：40%，均值约-75 dBm
• 群体2（差基站）：60%，均值约-95 dBm

箱线图对比：

• 群体1的箱子位置高（信号强）
• 群体2的箱子位置低（信号弱）
• 两个群体几乎不重叠

业务意义：

• 存在两个性能差异很大的基站群体
• 应该分别分析和优化
• 群体2（差基站）需要优先优化

左下图 - Q-Q图（S形曲线）：

关键观察：

• 点形成S形曲线
• 这是双峰分布的典型特征
• 左下部分：点低于参考线
• 右上部分：点高于参考线

说明文字： " S形曲线 -> 双峰分布特征"

右下图 - 检验结果和业务解读：

Shapiro-Wilk检验：

统计量: 0.9340p值: < 0.000001结论: 显著偏离正态分布

GMM聚类结果：

群体1（好基站）:  均值: -75 dBm  数量: 80个群体2（差基站）:  均值: -95 dBm  数量: 120个

业务解读：

• RSRP呈现"双峰分布"
• 存在两个明显的基站群体
• 好基站群体信号强
• 差基站群体信号弱
• 需要对差基站群体进行覆盖优化

09 结合通信运维的深度思考

9.1 非正态分布的影响

影响1：统计检验失效

问题：为什么t检验结果不稳定？

答案：掉话率不符合正态分布，不能使用t检验

后果：

• p值不可靠
• 结论可能是错误的
• 可能得出"优化有效"的错误结论

解决方案：使用非参数检验

• Mann-Whitney U检验：替代独立样本t检验
• Wilcoxon符号秩检验：替代配对样本t检验
• Kruskal-Wallis检验：替代单因素ANOVA

影响2：均值误导

问题：为什么平均掉话率1.5%不能代表大多数基站？

答案：掉话率右偏，均值被高值拉高

举例：

• 180个基站：掉话率0.8%（中位数）
• 20个基站：掉话率6%（异常值）
• 均值：(180 × 0.8 + 20 × 6) / 200 = 1.5%
• 均值是中位数的近2倍！

解决方案：

• 使用中位数描述中心趋势
• 使用四分位数描述离散程度
• 识别并处理异常值

影响3：掩盖真相

问题：为什么整体指标看起来正常，但用户投诉多？

答案：少数"隐形杀手"基站被整体均值掩盖

场景：

• 整体掉话率：1.5%（看起来还可以）
• 但20个基站掉话率 > 5%
• 这些基站覆盖的区域用户感知很差
• 但被整体指标"掩盖"了

解决方案：

• 进行正态分布检验
• 识别非正态分布
• 使用分位数法识别异常值
• 对异常基站进行重点优化

9.2 解决方案

方案1：数据转换

对数转换（适用于右偏数据）：

# 对掉话率进行对数转换drop_rate_transformed = np.log(drop_rate + 1)# 再次检验正态性shapiro_stat, shapiro_p = shapiro(drop_rate_transformed)

效果：

• 可以使右偏数据更接近正态分布
• 然后可以使用参数统计方法

方案2：使用非参数检验

方案3：分群分析

对于双峰分布：

from sklearn.mixture import GaussianMixture# 拟合高斯混合模型gmm = GaussianMixture(n_components=2)gmm.fit(rsrp.reshape(-1, 1))# 预测每个基站的群体labels = gmm.predict(rsrp.reshape(-1, 1))# 分别分析两个群体group1 = rsrp[labels == 0]group2 = rsrp[labels == 1]

方案4：使用稳健统计量

9.3 实施建议

1. 分析前的正态性检验

每次进行统计分析前：

• 绘制直方图和Q-Q图
• 进行Shapiro-Wilk检验
• 检查偏度和峰度

2. 根据检验结果选择方法

3. 报告时说明分布特征

在分析报告中：

• 说明数据的分布类型
• 说明选择的检验方法及其理由
• 报告偏度和峰度
• 对于非正态分布，报告中位数

10 本地实战：运行代码

10.1 环境安装

# 安装Python依赖pip install pandas numpy matplotlib seaborn scikit-learn scipy openpyxl

10.2 运行代码

# 进入文章目录cd"011-用Python正态分布检验识别5G基站隐形杀手"# 运行代码生成数据和图表python code.py

运行后会生成以下文件：

• 011_5G_KPI_Distribution_Data.xlsx - 模拟的KPI数据
• images/011_distribution_test_overview.png - 综合分布检验图
• images/011_qq_plot_analysis.png - Q-Q图分析
• images/011_drop_rate_detailed_analysis.png - 掉话率详细分析
• images/011_rsrp_bimodal_analysis.png - RSRP双峰分布分析

11 总结

11.1 本篇核心要点

✅ 正态分布检验是统计分析的第一步，避免用错方法

✅ Shapiro-Wilk检验是最常用的正态性检验，p < 0.05说明不符合正态分布

✅ Q-Q图是可视化检验，点偏离参考线说明不符合正态分布

✅ 偏度 > 0.5说明右偏，偏度 < -0.5说明左偏

✅ 双峰分布暗示存在多个子群体，需要分群分析

✅ 非正态数据应使用非参数检验或数据转换

✅ 右偏数据使用中位数比均值更稳健

11.2 方法选择指南

11.3 进阶思考

问题1：如果样本量很大（> 5000），Shapiro-Wilk检验p值总是很小怎么办？答案：大样本时，Shapiro-Wilk检验过于灵敏，可以主要看Q-Q图和偏度、峰度。

问题2：数据轻微偏态（偏度0.3-0.5），能用t检验吗？答案：t检验对轻微偏离正态具有一定的稳健性，可以使用，但最好用非参数检验验证。

问题3：如何让数据符合正态分布？答案：可以尝试数据转换（对数、平方根、Box-Cox），或使用非参数检验。

12 资源说明

如需本文素材（完整代码、excel格式的模拟数据集、生成的可视化图片等），欢迎加v：gprshome201101联系作者获取，我打包发给您。

13 作者信息

作者：爱卫生，微信：gprshome201101，20年移动通信核心网老兵。主打5GC、IMS与AI在通信行业中的应用。欢迎加v交流。

【免责声明】本文代码仅用于学习交流，实际应用中请结合现网数据和环境进行适配。数据分析结果仅供参考，优化决策请遵循运营商标准流程。