【生存分析机器学习】Python03-Cox比例风险模型(CoxPH)及可视化
- 2026-01-31 16:15:10
【生存分析机器学习】Python03-Cox比例风险模型(CoxPH)及可视化生存分析机器学习 
03-Cox比例风险模型（CoxPH）及可视化 Python（标准化代码） 
01 概念、原理、思想、应用 02 操作流程 
03 代码及操作演示与功能解析 
！！！可加我粉丝群！！！ 【医学统计数据分析】工作室“粉丝群” 
01 【临床】粉丝群 02 【公卫】粉丝群 03 【生信】粉丝群 
概念：半参数模型，用于分析因素对生存时间的影响，假设风险比例恒定。
原理：模型为h(t|X) = h0(t) * exp(βX)，其中h0(t)是基线风险函数。参数β通过最大化部分似然估计。
思想：分离基线风险和协变量效应，不假设风险函数形式。
应用：多因素生存分析，控制混杂因素。
可视化：森林图显示风险比（HR）和置信区间；生存曲线；风险函数图。
公共卫生意义：评估多种风险因素对疾病预后的影响，如流行病学研究。
-数据预处理：
-模型构建：
-训练：
-评估：
-可视化：
-保存结果：
生存分析机器学习模型主要分为传统统计扩展模型、树基集成模型和深度学习模型三大类，它们通过不同机制处理删失数据并预测事件发生时间。评价方法则聚焦于区分能力、校准效果和临床实用性，核心指标包括一致性指数（C-index）、Brier分数和时间依赖ROC曲线等。
# pip install pandas numpy matplotlib seaborn scikit-learn lifelines scipyimport osimport pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScalerfrom lifelines import CoxPHFitterfrom lifelines.utils import concordance_indexfrom lifelines.statistics import proportional_hazard_testfrom lifelines.plotting import add_at_risk_countsimport scipy.stats as statsfrom sklearn.metrics import roc_curve, aucfrom sklearn.calibration import calibration_curveimport warningswarnings.filterwarnings('ignore')# 设置中文字体和输出目录plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei']plt.rcParams['axes.unicode_minus'] = False# 创建结果文件夹desktop_path = os.path.join(os.path.expanduser("~"), "Desktop")results_dir = os.path.join(desktop_path, "Results模型-cox-comprehensive")os.makedirs(results_dir, exist_ok=True)# 1. 数据准备和预处理def load_and_preprocess_data():""" 加载和预处理数据 注意：这里假设您有一个名为'示例数据.xlsx'的Excel文件 如果没有实际数据，我们将创建模拟数据 """ try:# 尝试读取实际数据 data = pd.read_excel(os.path.join(desktop_path, "示例数据.xlsx"), sheet_name="示例数据")print("成功读取示例数据") except:# 创建模拟数据print("未找到示例数据，创建模拟数据...") np.random.seed(2025) n_samples = 500 data = pd.DataFrame({'时间': np.random.exponential(100, n_samples),'结局': np.random.choice([0, 1], n_samples, p=[0.7, 0.3]),'指标1': np.random.normal(50, 10, n_samples),'指标2': np.random.normal(25, 5, n_samples),'指标3': np.random.normal(100, 20, n_samples),'指标4': np.random.normal(10, 2, n_samples),'指标5': np.random.normal(75, 15, n_samples),'指标6': np.random.normal(30, 6, n_samples),'指标7': np.random.normal(60, 12, n_samples),'指标8': np.random.choice(['A', 'B', 'C'], n_samples),'肥胖程度': np.random.choice(['正常', '超重', '肥胖'], n_samples),'教育水平': np.random.choice(['小学', '中学', '大学'], n_samples),'血型': np.random.choice(['A', 'B', 'O', 'AB'], n_samples) })# 确保时间变量为正数 data['时间'] = np.abs(data['时间'])# 数据预处理 data['时间'] = pd.to_numeric(data['时间'], errors='coerce') data['结局'] = pd.to_numeric(data['结局'], errors='coerce') data['结局'] = data['结局'].fillna(0).astype(int)# 处理分类变量 categorical_cols = ['指标8', '肥胖程度', '教育水平', '血型']for col in categorical_cols:if col in data.columns: data[col] = data[col].astype('category')# 删除缺失值 data = data.dropna()print(f"数据维度: {data.shape}")print(f"结局分布:\n{data['结局'].value_counts()}")return data# 2. 描述性统计分析def descriptive_analysis(data, results_dir):"""生成描述性统计分析"""print("\n=== 描述性统计分析 ===")# 数值变量描述 numeric_cols = data.select_dtypes(include=[np.number]).columns numeric_cols = [col for col in numeric_cols if col not in ['时间', '结局']] desc_stats = data[numeric_cols].describe().T desc_stats['missing'] = data[numeric_cols].isnull().sum()# 分类变量描述 categorical_cols = data.select_dtypes(include=['category']).columns cat_stats = {}for col in categorical_cols: cat_stats[col] = data[col].value_counts()# 按结局分组的描述if len(data['结局'].unique()) > 1: grouped_stats = data.groupby('结局')[numeric_cols].mean()# 保存结果 desc_stats.to_csv(os.path.join(results_dir, "数值变量描述性统计.csv")) with open(os.path.join(results_dir, "分类变量统计.txt"), "w") as f:for col, counts in cat_stats.items(): f.write(f"\n{col}:\n{counts}\n")return desc_stats, cat_stats# 3. 划分训练集和测试集def split_data(data, test_size=0.3, random_state=2025):"""划分训练集和测试集""" train_data, test_data = train_test_split( data, test_size=test_size, random_state=random_state, stratify=data['结局'] )print(f"训练集样本数: {len(train_data)}")print(f"测试集样本数: {len(test_data)}")return train_data, test_data# 5. 模型性能评估def evaluate_model(cph, train_data, test_data, predictor_cols, results_dir):"""评估模型性能"""print("\n=== 模型性能评估 ===")# 训练集C-index train_scores = cph.predict_partial_hazard(train_data[predictor_cols]) train_cindex = concordance_index( train_data['时间'], -train_scores, # 风险分数越高，生存时间越短 train_data['结局'] )# 测试集C-index test_scores = cph.predict_partial_hazard(test_data[predictor_cols]) test_cindex = concordance_index( test_data['时间'], -test_scores, test_data['结局'] )print(f"训练集C-index: {train_cindex:.3f}")print(f"测试集C-index: {test_cindex:.3f}")# 时间依赖性ROC曲线 time_points = [12, 24, 36] # 1年、2年、3年 auc_values = calculate_time_dependent_roc(test_data, test_scores, time_points, results_dir)# Brier分数 brier_scores = calculate_brier_score(test_data, test_scores, time_points, results_dir)return {'train_cindex': train_cindex,'test_cindex': test_cindex,'auc_values': auc_values,'brier_scores': brier_scores }def calculate_time_dependent_roc(test_data, risk_scores, time_points, results_dir):"""计算时间依赖性ROC曲线"""print("\n=== 时间依赖性ROC曲线 ===") auc_values = {} roc_data = {}for time_point in time_points:# 简化版时间依赖性ROC - 使用风险分数在特定时间点的预测# 在实际应用中，您可能需要使用更复杂的方法如ROC from survivalROC包# 创建二元标签：在时间点前发生事件为1，否则为0 y_true = ((test_data['时间'] <= time_point) & (test_data['结局'] == 1)).astype(int)if y_true.sum() > 0: # 确保有阳性样本 fpr, tpr, _ = roc_curve(y_true, risk_scores) roc_auc = auc(fpr, tpr) auc_values[time_point] = roc_auc roc_data[time_point] = {'fpr': fpr, 'tpr': tpr, 'auc': roc_auc}print(f"{time_point}个月AUC: {roc_auc:.3f}")else:print(f"{time_point}个月: 无事件发生，无法计算AUC") auc_values[time_point] = np.nan# 绘制ROC曲线 plot_time_dependent_roc(roc_data, results_dir)return auc_valuesdef calculate_brier_score(test_data, risk_scores, time_points, results_dir):"""计算Brier分数"""print("\n=== Brier分数计算 ===") brier_scores = {}for time_point in time_points:# 简化版Brier分数计算# 在实际应用中，您可能需要使用更专业的生存分析包 observed = ((test_data['时间'] <= time_point) & (test_data['结局'] == 1)).astype(int) predicted = 1 - (risk_scores - risk_scores.min()) / (risk_scores.max() - risk_scores.min()) brier_score = np.mean((observed - predicted) ** 2) brier_scores[time_point] = brier_scoreprint(f"{time_point}个月Brier分数: {brier_score:.3f}")# 保存Brier分数 brier_df = pd.DataFrame(list(brier_scores.items()), columns=['Time', 'Brier_Score']) brier_df.to_csv(os.path.join(results_dir, "Brier分数.csv"), index=False)return brier_scores# 6. 可视化分析def create_visualizations(cph, train_data, test_data, predictor_cols, performance_metrics, results_dir):"""创建所有可视化图表"""print("\n=== 创建可视化图表 ===")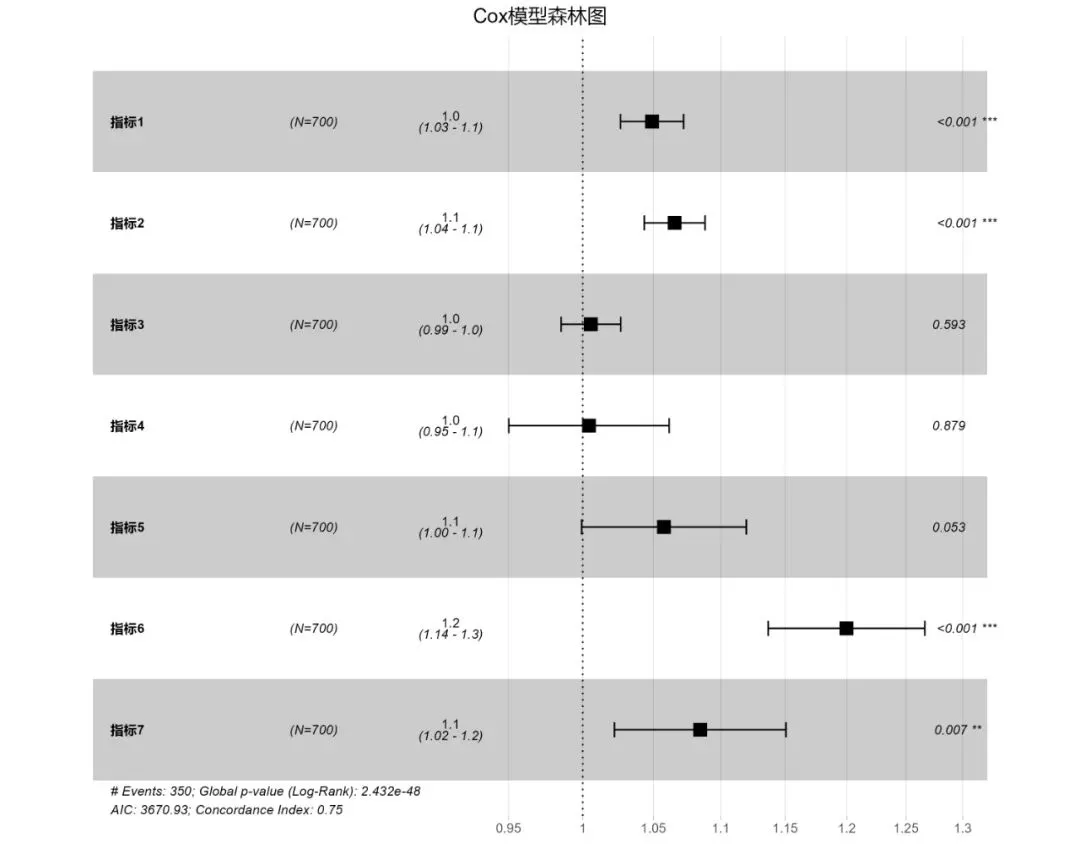# 6.1 森林图 plot_forest(cph, results_dir)# 6.2 生存曲线 plot_survival_curves(cph, train_data, results_dir)# 6.3 比例风险假设检验 check_proportional_hazards(cph, train_data, predictor_cols, results_dir)# 6.4 校准曲线 plot_calibration_curve(test_data, cph.predict_partial_hazard(test_data[predictor_cols]), results_dir)# 6.5 风险分层可视化 plot_risk_stratification(test_data, cph.predict_partial_hazard(test_data[predictor_cols]), results_dir)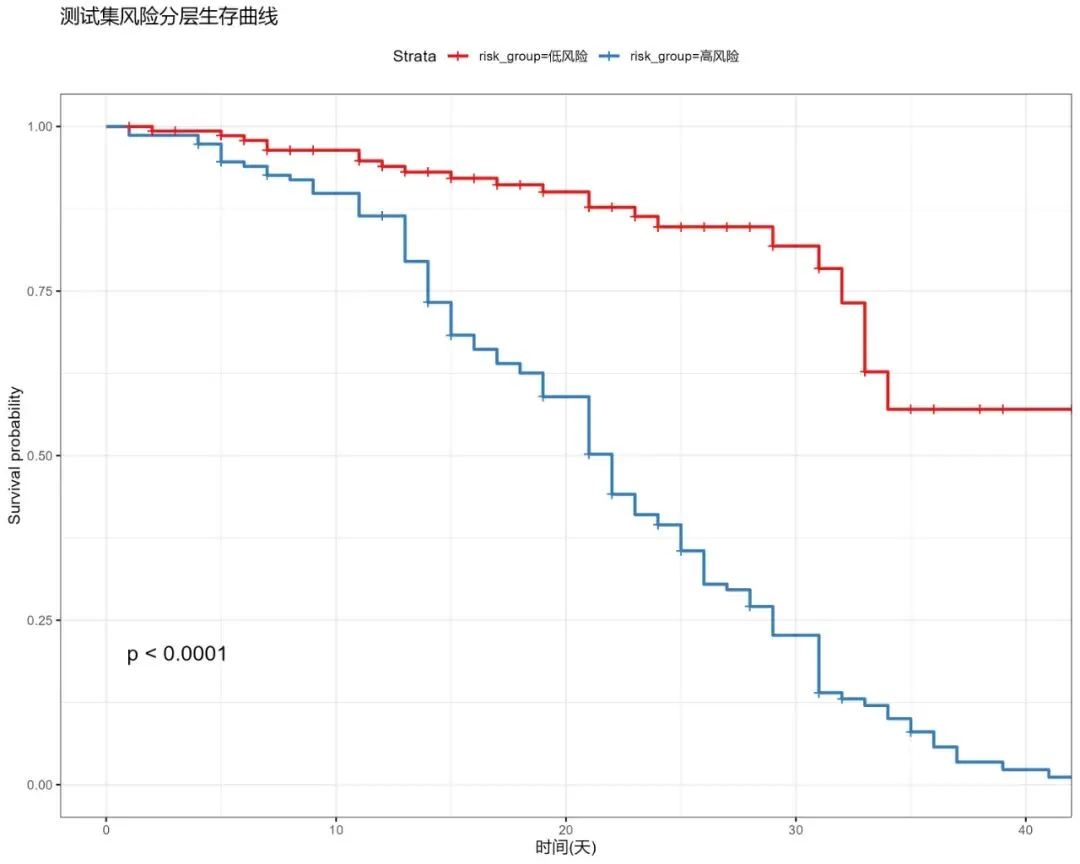# 6.6 临床决策曲线分析 plot_decision_curve_analysis(test_data, cph.predict_partial_hazard(test_data[predictor_cols]), results_dir)# 6.7 列线图 plot_nomogram(cph, predictor_cols, results_dir)def plot_forest(cph, results_dir):"""绘制森林图""" plt.figure(figsize=(10, 8))# 获取系数和置信区间 summary = cph.summary coefs = summary['coef'] hazards = np.exp(coefs) lower_ci = np.exp(summary['coef lower 95%']) upper_ci = np.exp(summary['coef upper 95%']) p_values = summary['p']# 创建森林图 variables = summary.index y_pos = np.arange(len(variables)) plt.errorbar(hazards, y_pos, xerr=[hazards - lower_ci, upper_ci - hazards], fmt='o', capsize=5, capthick=2, markersize=8) plt.axvline(x=1, color='red', linestyle='--', alpha=0.7) plt.yticks(y_pos, variables) plt.xlabel('风险比 (HR)') plt.title('Cox模型森林图') plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "森林图.jpg"), dpi=300, bbox_inches='tight') plt.close()def plot_survival_curves(cph, train_data, results_dir):"""绘制生存曲线""" plt.figure(figsize=(12, 8))# 绘制基线生存函数 cph.baseline_survival_.plot(figsize=(12, 8)) plt.xlabel('时间') plt.ylabel('生存概率') plt.title('Cox模型基线生存曲线') plt.grid(True, alpha=0.3) plt.legend(['基线生存函数']) plt.tight_layout() plt.savefig(os.path.join(results_dir, "生存曲线.jpg"), dpi=300, bbox_inches='tight') plt.close()def check_proportional_hazards(cph, train_data, predictor_cols, results_dir):"""比例风险假设检验"""print("\n=== 比例风险假设检验 ===") try:# 使用lifelines的比例风险检验 results = proportional_hazard_test(cph, train_data[predictor_cols], time_transform='rank')print("比例风险检验结果:")print(results.summary)# 保存检验结果 results.summary.to_csv(os.path.join(results_dir, "比例风险检验结果.csv")) except Exception as e:print(f"比例风险检验出错: {e}")def plot_calibration_curve(test_data, risk_scores, results_dir):"""绘制校准曲线""" plt.figure(figsize=(10, 8))# 简化版校准曲线# 在实际应用中，您可能需要使用更专业的方法# 将风险分数转换为生存概率 survival_probs = 1 - (risk_scores - risk_scores.min()) / (risk_scores.max() - risk_scores.min())# 创建校准数据 prob_true, prob_pred = calibration_curve( test_data['结局'], survival_probs, n_bins=10, strategy='quantile' ) plt.plot(prob_pred, prob_true, 's-', label='校准曲线') plt.plot([0, 1], [0, 1], '--', color='gray', label='理想校准') plt.xlabel('预测生存概率') plt.ylabel('实际生存概率') plt.title('校准曲线') plt.legend() plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "校准曲线.jpg"), dpi=300, bbox_inches='tight') plt.close()def plot_risk_stratification(test_data, risk_scores, results_dir):"""风险分层可视化""" plt.figure(figsize=(12, 8))# 根据风险分数中位数分层 risk_median = np.median(risk_scores) test_data = test_data.copy() test_data['risk_group'] = np.where(risk_scores > risk_median, '高风险', '低风险')# 使用lifelines绘制分层生存曲线 from lifelines import KaplanMeierFitter kmf = KaplanMeierFitter() plt.figure(figsize=(12, 8))for group in ['低风险', '高风险']: group_data = test_data[test_data['risk_group'] == group] kmf.fit(group_data['时间'], group_data['结局'], label=group) kmf.plot_survival_function() plt.xlabel('时间') plt.ylabel('生存概率') plt.title('测试集风险分层生存曲线') plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "风险分层生存曲线.jpg"), dpi=300, bbox_inches='tight') plt.close()def plot_decision_curve_analysis(test_data, risk_scores, results_dir):"""临床决策曲线分析""" plt.figure(figsize=(10, 8))# 简化版DCA thresholds = np.linspace(0.01, 0.99, 50) net_benefits = []for threshold in thresholds:# 根据阈值决定治疗 treat_by_model = risk_scores > np.quantile(risk_scores, threshold) true_positives = np.sum(treat_by_model & (test_data['结局'] == 1)) false_positives = np.sum(treat_by_model & (test_data['结局'] == 0)) n = len(test_data) net_benefit = (true_positives / n) - (false_positives / n) * (threshold / (1 - threshold)) net_benefits.append(net_benefit) plt.plot(thresholds, net_benefits, 'b-', linewidth=2, label='模型') plt.axhline(y=0, color='gray', linestyle='--', label='不治疗')# 所有治疗策略 event_rate = test_data['结局'].mean() treat_all_benefit = [event_rate - (1 - event_rate) * (t / (1 - t)) for t in thresholds] plt.plot(thresholds, treat_all_benefit, 'r--', linewidth=2, label='全部治疗') plt.xlabel('决策阈值') plt.ylabel('标准化净获益') plt.title('临床决策曲线分析 (DCA)') plt.legend() plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "临床决策曲线.jpg"), dpi=300, bbox_inches='tight') plt.close()def plot_nomogram(cph, predictor_cols, results_dir):"""绘制列线图（简化版）""" plt.figure(figsize=(15, 10))# 获取模型系数 coefficients = cph.params_# 创建列线图数据 nomogram_data = pd.DataFrame({'Variable': predictor_cols,'Coefficient': coefficients,'HR': np.exp(coefficients) }).sort_values('Coefficient', key=abs, ascending=False)# 绘制水平条形图作为简化列线图 y_pos = np.arange(len(nomogram_data)) plt.barh(y_pos, nomogram_data['HR']) plt.yticks(y_pos, nomogram_data['Variable']) plt.xlabel('风险比 (HR)') plt.title('Cox模型列线图（风险比展示）')# 添加数值标签for i, v in enumerate(nomogram_data['HR']): plt.text(v + 0.01, i, f'{v:.2f}', va='center') plt.axvline(x=1, color='red', linestyle='--', alpha=0.7) plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "列线图.jpg"), dpi=300, bbox_inches='tight') plt.close()# 保存列线图数据 nomogram_data.to_csv(os.path.join(results_dir, "列线图数据.csv"), index=False)def plot_time_dependent_roc(roc_data, results_dir):"""绘制时间依赖性ROC曲线""" plt.figure(figsize=(10, 8)) colors = ['#4DAF4A', '#984EA3', '#FF7F00']for i, (time_point, data) in enumerate(roc_data.items()):if'fpr'in data and 'tpr'in data: plt.plot(data['fpr'], data['tpr'], color=colors[i], linewidth=2, label=f'{time_point}个月 (AUC = {data["auc"]:.2f})') plt.plot([0, 1], [0, 1], 'k--', alpha=0.5, label='随机分类') plt.xlabel('1 - 特异度') plt.ylabel('敏感度') plt.title('时间依赖性ROC曲线') plt.legend() plt.grid(True, alpha=0.3) plt.tight_layout() plt.savefig(os.path.join(results_dir, "时间ROC曲线.jpg"), dpi=300, bbox_inches='tight') plt.close()# 7. 保存结果和生成报告def save_results_and_report(cph, performance_metrics, train_data, test_data, results_dir):"""保存所有结果并生成报告"""print("\n=== 保存结果和生成报告 ===")# 7.1 保存模型性能指标 performance_df = pd.DataFrame([ ['训练集C-index', performance_metrics['train_cindex']], ['测试集C-index', performance_metrics['test_cindex']], ] + [[f'{time_point}个月AUC', auc_value]for time_point, auc_value in performance_metrics['auc_values'].items()], columns=['Metric', 'Value'] ) performance_df.to_csv(os.path.join(results_dir, "模型性能指标.csv"), index=False)# 7.2 保存模型系数 model_coefficients = cph.summary.reset_index().rename(columns={'index': 'variable'}) model_coefficients.to_csv(os.path.join(results_dir, "模型系数.csv"), index=False)# 7.3 生成文本报告 generate_text_report(performance_metrics, len(train_data), len(test_data), results_dir)# 7.4 保存工作空间 import joblib joblib.dump({'model': cph,'performance_metrics': performance_metrics,'train_data': train_data,'test_data': test_data }, os.path.join(results_dir, "分析环境.pkl"))def generate_text_report(performance_metrics, n_train, n_test, results_dir):"""生成文本报告""" report_content = f"""Cox比例风险模型综合分析报告================================数据概览--------训练集样本数: {n_train}测试集样本数: {n_test}模型性能指标-----------训练集C-index: {performance_metrics['train_cindex']:.3f}测试集C-index: {performance_metrics['test_cindex']:.3f}时间依赖性AUC值:"""for time_point, auc_value in performance_metrics['auc_values'].items(): report_content += f"{time_point}个月AUC: {auc_value:.3f}\n" report_content += f"""Brier分数:"""for time_point, brier_score in performance_metrics['brier_scores'].items(): report_content += f"{time_point}个月Brier分数: {brier_score:.3f}\n" report_content += f"""关键结论--------模型在测试集的区分能力(C-index): {performance_metrics['test_cindex']:.3f}平均Brier分数: {np.mean(list(performance_metrics['brier_scores'].values())):.3f}"""# 性能问题提示if performance_metrics['test_cindex'] < 0.5: report_content += """!!! 警告: 测试集C-index低于0.5，模型在测试集上表现不佳 !!!可能原因:- 训练集和测试集分布差异大- 模型过拟合- 数据预处理问题建议检查数据划分的随机性和数据质量。""" with open(os.path.join(results_dir, "综合分析报告.txt"), "w", encoding='utf-8') as f: f.write(report_content)# 主函数def main():print("开始Cox比例风险模型综合分析...")# 1. 数据准备和预处理 data = load_and_preprocess_data()# 2. 描述性统计分析 desc_stats, cat_stats = descriptive_analysis(data, results_dir)# 3. 划分训练集和测试集 train_data, test_data = split_data(data)# 4. 构建Cox比例风险模型 cph, predictor_cols = build_cox_model(train_data)# 5. 模型性能评估 performance_metrics = evaluate_model(cph, train_data, test_data, predictor_cols, results_dir)# 6. 可视化分析 create_visualizations(cph, train_data, test_data, predictor_cols, performance_metrics, results_dir)# 7. 保存结果和生成报告 save_results_and_report(cph, performance_metrics, train_data, test_data, results_dir)print(f"\n=== Cox比例风险模型综合分析已完成 ===")print(f"所有结果已保存到 {results_dir} 文件夹中。")print("包含的性能评价指标:")print("- 综合区分能力 (C-index)")print("- 时间依赖性ROC曲线 (AUC)")print("- Brier分数 (校准度)")print("- 临床决策曲线 (DCA)")print("- 风险分层分析")print("- 列线图")print(f"\n关键指标:")print(f"训练集C-index: {performance_metrics['train_cindex']:.3f}")print(f"测试集C-index: {performance_metrics['test_cindex']:.3f}")print(f"时间点AUC值: {', '.join([f'{auc_value:.3f}' for auc_value in performance_metrics['auc_values'].values()])}")print(f"平均Brier分数: {np.mean(list(performance_metrics['brier_scores'].values())):.3f}")if __name__ == "__main__": main()🔍Cox比例风险模型及可视化
概念：Cox比例风险模型是一种半参数模型，用于探讨多个变量对生存风险的影响，其核心是比例风险假设，即协变量对风险的影响随时间推移保持不变。
原理：模型形式为 $h(t|X) = h_0(t) \exp(\beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p)$。其中 $h_0(t)$ 是基线风险函数，$\exp(\beta)$ 表示风险比。参数 $\beta$ 通过最大化部分似然函数来估计。
思想：分离基线风险函数与协变量效应，无需指定 $h_0(t)$ 的具体形式，专注于研究变量对相对风险的影响。
应用：广泛用于流行病学队列研究和临床预后分析，例如分析年龄、治疗方式等多种因素对患者死亡风险的影响。
可视化：森林图：展示各变量的风险比及其置信区间。Schoenfeld残差图：用于检验比例风险假设是否成立。生存曲线：在设定协变量值后，可绘制预测的生存曲线。
医学统计数据分析分享交流SPSS、R语言、Python、ArcGis、Geoda、GraphPad、数据分析图表制作等心得。承接数据分析，论文返修，医学统计，机器学习，生存分析，空间分析，问卷分析业务。若有投稿和数据分析代做需求，可以直接联系我，谢谢！
“医学统计数据分析”公众号右下角；
找到“联系作者”，
可加我微信，邀请入粉丝群！
有临床流行病学数据分析
如（t检验、方差分析、χ2检验、logistic回归）、
（重复测量方差分析与配对T检验、ROC曲线）、
（非参数检验、生存分析、样本含量估计）、
（筛检试验：灵敏度、特异度、约登指数等计算）、
（绘制柱状图、散点图、小提琴图、列线图等）、
机器学习、深度学习、生存分析
等需求的同仁们，加入【临床】粉丝群。
疾控，公卫岗位的同仁，可以加一下【公卫】粉丝群，分享生态学研究、空间分析、时间序列、监测数据分析、时空面板技巧等工作科研自动化内容。
有实验室数据分析需求的同仁们，可以加入【生信】粉丝群，交流NCBI（基因序列）、UniProt（蛋白质）、KEGG（通路）、GEO（公共数据集）等公共数据库、基因组学转录组学蛋白组学代谢组学表型组学等数据分析和可视化内容。
或者可扫码直接加微信进群！！！
精品视频课程-“医学统计数据分析”视频号付费合集
在“医学统计数据分析”视频号-付费合集兑换相应课程后，获取课程理论课PPT、代码、基础数据等相关资料，请大家在【医学统计数据分析】公众号右下角，找到“联系作者”，加我微信后打包发送。感谢您的支持！！
本文来自网友投稿或网络内容，如有侵犯您的权益请联系我们删除，联系邮箱：wyl860211@qq.com 。
随机文章
-
10个月宝宝每天需要喝多少奶粉？
- Python超全电子书合集 | 16本python书籍(附PDF版),看完少走一半弯路--纯分享版!
- 你遇到的80个Python问题,答案都在这里了
- 247个Python经典有趣实例,代码齐全可复制,PDF版拿走即用
- 为什么我学Python的时候不知道这个APP!
- 拒绝当牛马!4个Python自动化办公神技!
- 只需指令,用AI来创建自己的python虚拟环境
- 存下吧少爷!Python入门必须要的“背单词”
- 新手学Python:80个超实用小实例,从入门到上瘾
- 这个库,让我的Python从“拖拉机”变“法拉利”!
- AI 的双向分化:光芯片挑战摩尔定律,Linux 之父拥抱“氛围编程”
