LLM大模型辅助PINN编程一鸣惊人,再登Nature!

1. 物理信息神经网络（PINN）的兴起

近年来，物理信息神经网络（Physics-Informed Neural Networks, PINN）成为计算科学与人工智能交叉领域的前沿方向。传统数值方法（如有限差分法、有限单元法）在高维、强非线性或反演问题中面临计算效率低、网格依赖性强等瓶颈。PINN通过将控制方程、边界条件等物理先验嵌入神经网络，以无网格方式实现微分方程求解，在流体力学、固体力学、传热学等领域展现出突破性潜力。其核心论文（引用超13,000次）开创了物理驱动深度学习的范式，成为Nature、CMAME等顶刊的研究热点。

2. 传统数值方法与机器学习的融合需求

有限差分法（FDM）和有限单元法（FEM）虽成熟但依赖离散化，难以处理复杂几何与多物理场耦合问题。机器学习（如CNN、GNN）虽具备强大的数据拟合能力，但缺乏物理可解释性。PINN通过融合物理定律与数据驱动，显著减少训练数据需求，提升泛化性能，并在参数反演、方程发现等逆问题中展现独特优势。此外，深度能量法（DEM）等变体进一步结合能量变分原理，为固体力学问题提供高效解决方案。

3. 大模型赋能科学计算的新机遇

以DeepSeek、ChatGPT为代表的大模型技术，正在颠覆传统科学编程模式。通过自然语言交互生成PINN代码，可加速复杂瞬态问题的求解流程。本课程结合大模型辅助编程，探索其在微分方程求解、代码调试及多任务优化中的应用，推动“AI for Science”的工程化落地。

4. 下个革命性的技术风口量子计算

量子计算对科学计算领域至关重要。传统超级计算机在模拟复杂分子结构、新材料属性等关键科学问题时已接近算力极限。量子计算凭借量子叠加与纠缠特性，有望实现对薛定谔方程等核心科学模型的高效求解，为催化反应、药物设计等领域带来革命性突破。开展针对性培训，能使科研人员掌握量子算法（如VQE、QAOA）与编程工具，将量子硬件转化为解决实际科学问题的强大工具，抢占前沿科研的制高点。这不仅是技能的提升，更是科研范式的革新。

1. 掌握PINN理论与传统数值方法的核心联系

理解固体力学、流体力学、传热学中的典型偏微分方程（如Navier-Stokes方程、弹性本构方程）及其数学分类（椭圆/抛物/双曲型）。

对比有限差分法、有限单元法与PINN的底层原理，揭示物理约束与数据驱动的协同机制。

2. 构建PINN与深度能量法的实践能力

从零实现一维谐振子、渗流、弹塑性力学等案例的PINN求解代码（基于PyTorch/DeepXDE/SciANN）。

掌握能量驱动损失函数设计、自动微分等关键技术，复现中科院一区顶刊（如CMAME）中的创新方法。

3. 探索多领域工业级应用场景

流体力学：层流模拟、涡旋捕捉与Nature子刊级diffusion-reaction模拟。

固体力学：超弹性材料大变形、弹塑性问题与能量法优化。

反问题：材料参数辨识、隐藏物理规律发现。

4. 精通开源工具链与大模型辅助编程

熟练使用DeepXDE、SciANN等PINN专用库，配置复杂边界条件与多物理场耦合。

利用DeepSeek、ChatGPT生成高鲁棒性PINN代码，解决瞬态偏微分方程问题。

5. 培养跨学科研究与创新能力

通过顶刊论文复现（如CMAME、Computers and Geotechnics）与代码对比，深化对物理编码、因果约束、混合变量方案等前沿方向的理解。

为计算力学、工业仿真、AI辅助设计等领域的科研与工程实践提供方法论支持。

本课程旨在打通物理建模、数值计算与深度学习的知识壁垒，培养兼具理论深度与工程能力的复合型人才，推动智能科学计算在工业4.0与数字孪生中的创新应用。

Day 1 什么是微分方程（固体、流体、传热）？什么是有限差分法和有限单元法？和机器学习有什么联系？

1. 学会偏微分方程手动推导

0.0. 一般形式的微分方程推导

0.1 散度算子与平衡项的关系

0.2. 输运方程的对流项

0.3 偏微分方程的三种形式：强形式、弱形式、变分形式

1.1. 固体力学的偏微分方程

1.1.1. 平衡方程

1.1.2. 线弹性本构

1.1.3. 超弹性本构

1.1.4. 塑性本构

1.2. 流体力学的偏微分方程

1.2.1. 无黏、无旋的势流方程

1.2.2. 忽略黏性效应的欧拉方程

1.2.3. 不可压缩纳维-斯托克斯方程

1.3. 传热学的偏微分方程

1.3.1. 稳态热传导

1.3.2. 瞬态热传导

1.4. 一般形式的偏微分方程

1.4.1. 椭圆偏微分方程

1.4.2. 抛物偏微分方程

1.4.3. 双曲偏微分方程

2. 偏微分方程数值解

2.1. 有限差分法原理

2.2. 有限单元法原理

2.3. 实战演练：使用COMSOL求解固体力学和渗流，保存数据

2.4. 实战演练：使用Abaqus求解弹塑性固体力学，保存数据

3. 使用Python写一个机器学习的程序

3.1. 三种运行Python程序的方法

3.2. 常用科学计算库：Numpy和Scipy

3.3. 机器学习的万能python库：scikit-learn

3.4. 如何在Ubuntu系统上运行python程序

Day 2 什么是深度学习？什么是物理数据双驱动神经网络PINN？

4. 数据驱动深度神经网络

4.1 激活函数

4.2 神经元

4.3 自动微分方法

4.4 损失函数的构建与正则化

4.5 最优化方法

4.6. 实践：基于Pytorch建立深度神经网络模型并调优

5. 深度学习进阶

5.1 卷积神经网络CNN（为什么使用CNN？）

5.2 循环神经网络RNN

5.2.1. 长短记忆神经网络LSTM

5.2.2. 门控循环单元网络GRU

5.3. 图神经网络GNN（居然与CNN一模一样？）

5.4. Transformer （Attention is all you need！ ）

6. PINN=数据+PDE方程，数据需求锐减！泛化性能提升！

从零开始构建一维谐振子物理信息神经网络（Physics-Informed Neural Networks, PINN）为核心目标，系统讲解如何将物理定律与深度学习结合，实现微分方程的高效求解与物理系统建模。课程从一维谐振子的动力学方程出发，剖析PINN的核心思想：通过神经网络隐式编码控制方程、初始/边界条件等物理约束，将微分方程求解转化为损失函数优化的机器学习问题。学习者将逐步掌握谐振子问题的数学建模方法，利用Python和深度学习框架（如PyTorch）搭建神经网络架构，设计融合数据驱动项与物理残差项（如运动方程残差）的复合损失函数，并通过自动微分技术计算高阶导数，实现从随机初始化到物理规律自洽的模型训练。

Day 3 PINN引用一万三论文详解+深度能量法+ PINN的python库Deep XDE讲解

7. 物理信息神经网络：一个用于解决涉及非线性偏微分方程的正问题和逆问题的深度学习框架，一万三千次引用的论文讲解和复现

PINN开山之作：Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations

1.1 传统数值方法的瓶颈（网格生成、高维问题、反问题不适定性）

1.2 深度学习的优势与局限：数据驱动与物理规律缺失

1.3 PINN的诞生：物理原理与数据智能的深度融合

一、 引言：求解PDE的范式转移

1.1 传统数值方法的瓶颈（网格生成、高维问题、反问题不适定性）

1.2 深度学习的优势与局限：数据驱动与物理规律缺失

1.3 PINN的诞生：物理原理与数据智能的深度融合

二、 PINN的核心机理与数学基础

2.1 框架总览：将物理域作为神经网络的输入空间

2.2 损失函数构造：物理残差、初始/边界条件与实测数据的多目标平衡

2.3 关键技术：自动微分为何是高效计算PDE高阶导数的核心

三、 PINN求解正问题：以Burgers方程为例

3.1 问题描述：强非线性与激波现象的挑战

3.2 网络架构设计与训练技巧

3.3 结果分析：与高精度数值解的比较及泛化能力验证

四、 PINN求解反问题：以参数辨识为例

4.1 问题定义：从稀疏观测数据中学习隐藏的PDE系数

4.2 可微学习机制：物理模型与神经网络参数的联合优化

4.3 案例演示：材料属性或未知物理规律的反演

五、 进阶应用与挑战展望

5.1 复杂场景拓展：Navier-Stokes方程与跨尺度问题

5.2 当前挑战：训练难度、收敛性及计算成本分析

5.3 未来方向：优化算法、多保真度融合与物理机理模型

8. 通过机器学习求解计算力学偏微分方程的能量方法：概念、实现和应用

深度能量/深度里兹法物理数据双驱动网络 Deep energy method/Deep Ritz method，DEM，DRM，中科院一区TOP数值计算顶刊CMAME：An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications

一、 引言：当能量变分原理遇见深度学习

1.1 计算力学的核心：从偏微分方程到能量极小化原理

1.2 传统有限元方法的局限与无网格求解的需求

1.3 新范式：用神经网络参数化力学场，将物理规律作为优化目标

二、 能量法的核心理论：从物理原理到损失函数

2.1 理论基础：最小势能原理与深度学习优化目标的数学同构性

2.2 框架构建：如何将总势能泛函转化为神经网络的训练目标

2.3 优势解析：为何能量法能天然满足物理约束并规避离散困难

三、 实现路径：损失函数设计与自动微分技术

3.1 损失函数设计：应变能主导的物理约束与边界条件的嵌入

3.2 关键引擎：自动微分技术在精确计算能量泛函梯度中的作用

3.3 实现流程：从场参数化到模型训练的全链路解析

四、 典型案例分析：从线弹性到材料非线性

4.1 案例一：弹性力学静动态问题求解

4.2 案例二：超弹性材料大变形分析

4.3 性能对比：与数据驱动模型及传统有限元法的优势对比

五、 方法总结与前沿展望

5.1 方法优势总结：预测精度、计算效率与外推能力

5.2 当前挑战与局限性分析

9. PINN库：DeepXDE讲解

第一章：DeepXDE入门——核心概念与环境搭建

1.1 引言：为何选择DeepXDE？—— 高效PINN开发的关键特性

1.2 环境配置指南：在本地与云端快速配置DeepXDE运行环境

1.3 初识核心API：dde.data、dde.geometry、dde.nn模块概览

1.4 第一个PINN实例：求解一维泊松方程的完整工作流

第二章：几何定义与边界条件设置——构建物理计算域

2.1 几何定义详解：一维区间(Interval)与二维矩形(Rectangle)的创建

2.2 进阶几何：复杂几何（圆形、多边形）与时空域(TimeDomain)的处理

2.3 边界条件编码：DirichletBC、NeumannBC、RobinBC的API用法

2.4 初始条件编码：IC及其在时空问题中的应用

第三章：定义控制方程——PDE残差的灵活表达

3.1 使用Lambda函数快速定义PDE残差（推荐入门）

3.2 自定义偏微分算子：处理复杂或高阶微分方程

3.3 多未知数方程组（PDE系统）的定义方法

3.4 反问题中PDE参数的定义与设置

第四章：神经网络架构配置与优化——平衡效率与精度

4.1 网络架构选择：前馈网络（FNN）与修改版（MFNN）等

4.2 激活函数实战：从tanh到自适应激活函数（如sin）的性能对比

4.3 权重初始化策略：Glorot normal与 He normal的影响

4.4 损失函数配置：平衡PDE残差、边界条件与数据项的权重策略

第五章：综合实战：从一维到高维经典案例

5.1 案例一（一维）：Burgers方程激波捕捉

5.2 案例二（二维）：稳态/非稳态热传导方程求解

5.3 案例三（反问题）：从稀疏数据中反演拉普拉斯方程源项

5.4 案例四（高维）：参数化PDE的快速求解

Day 4 PINN在流体力学中的应用 + Nature子刊详解

10. 中科院一区论文与代码复现：渗流

中科院一区顶刊论文复现，A physics-informed data-driven approach for consolidation analysis

第一章：DeepXDE入门——核心概念与环境搭建

1.1 引言：为何选择DeepXDE？—— 高效PINN开发的关键特性

1.2 环境配置指南：在本地与云端快速配置DeepXDE运行环境

1.3 初识核心API：dde.data、dde.geometry、dde.nn模块概览

1.4 第一个PINN实例：求解一维泊松方程的完整工作流

第二章：几何定义与边界条件设置——构建物理计算域

2.1 几何定义详解：一维区间(Interval)与二维矩形(Rectangle)的创建

2.2 进阶几何：复杂几何（圆形、多边形）与时空域(TimeDomain)的处理

2.3 边界条件编码：DirichletBC、NeumannBC、RobinBC的API用法

2.4 初始条件编码：IC及其在时空问题中的应用

第三章：定义控制方程——PDE残差的灵活表达

3.1 使用Lambda函数快速定义PDE残差（推荐入门）

3.2 自定义偏微分算子：处理复杂或高阶微分方程

3.3 多未知数方程组（PDE系统）的定义方法

3.4 反问题中PDE参数的定义与设置

第四章：神经网络架构配置与优化——平衡效率与精度

4.1 网络架构选择：前馈网络（FNN）与修改版（MFNN）等

4.2 激活函数实战：从tanh到自适应激活函数（如sin）的性能对比

4.3 权重初始化策略：Glorot normal与 He normal的影响

4.4 损失函数配置：平衡PDE残差、边界条件与数据项的权重策略

第五章：综合实战：从一维到高维经典案例

5.1 案例一（一维）：Burgers方程激波捕捉

5.2 案例二（二维）：稳态/非稳态热传导方程求解

5.3 案例三（反问题）：从稀疏数据中反演拉普拉斯方程源项

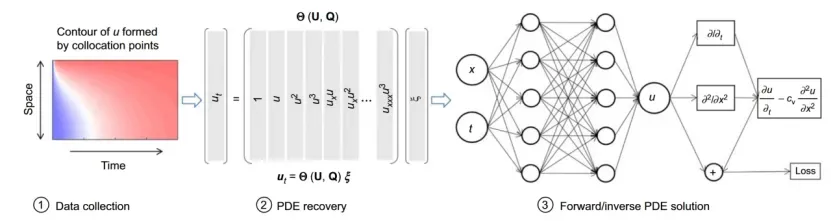
11. 物理信息网络求解不可压缩层流的深度学习问题

近年来，基于物理的深度学习引起了人们对解决计算物理问题的极大兴趣，其基本概念是嵌入物理定律来约束/通知神经网络，需要更少的数据来训练可靠的模型。这可以通过将物理方程的残差纳入损失函数来实现。通过最小化损失函数，网络可以近似解。本文提出了一种用于流体动力学的物理信息神经网络（PINN）的混合变量方案，并将其应用于模拟低雷诺数下的稳态和瞬态层流。参数研究表明，混合变量方案可以提高PINN的可训练性和求解精度。还将所提出的PINN方法预测的速度场和压力场与参考数值解进行了比较。仿真结果表明，所提出的PINN在高精度流体流动模拟方面具有巨大的潜力。

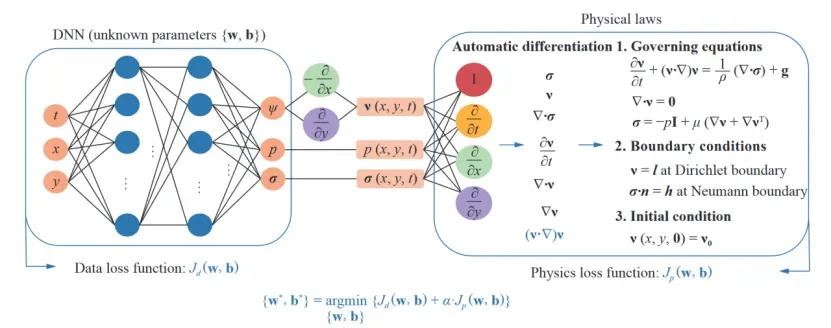
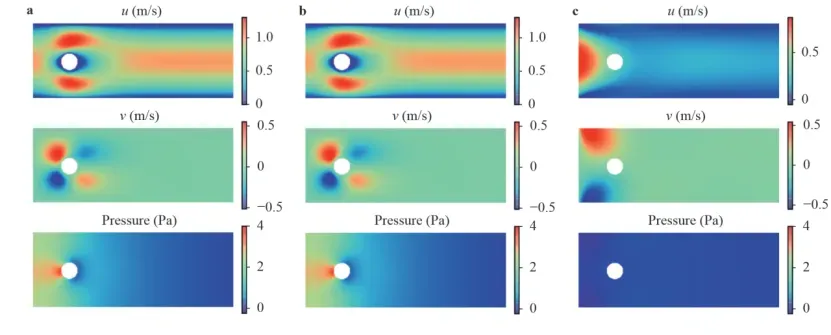
https://github.com/Raocp/PINN-laminar-flow/blob/master/PINN_steady/SteadyFlowCylinder_mixed.py

12. CMAME顶刊：考虑因果关系的流体力学PINN改进+学习用JAX实现PINN

中科院一区TOP数值计算顶刊CMAME：Respecting causality for training physics-informed neural networks

第一章：引言

1.1 研究背景：计算物理与深度学习融合的趋势

1.2 物理信息神经网络（PINN）基本原理：物理约束与损失函数

1.3 流体动力学模拟中的挑战与PINN的优势

1.4 本文主要工作与创新点：提出一种混合变量PINN方案

第二章：混合变量物理信息神经网络方法

2.1 控制方程：低雷诺数流动的Navier-Stokes方程

2.2 传统PINN方法在流体模拟中的局限性

2.3 混合变量方案的构建与理论框架

2.4 网络架构与损失函数设计

第三章：数值实验与讨论

3.1 实验设置：稳态与瞬态层流算例

3.2 参数研究：混合变量方案对可训练性与精度的影响

3.3 结果对比：速度场/压力场的PINN预测与参考解可视化比较

3.4 误差分析与讨论

第四章：结论与展望

4.1 研究结论总结

4.2 所提方法的优势与潜在应用价值

4.3 当前局限性与未来工作方向

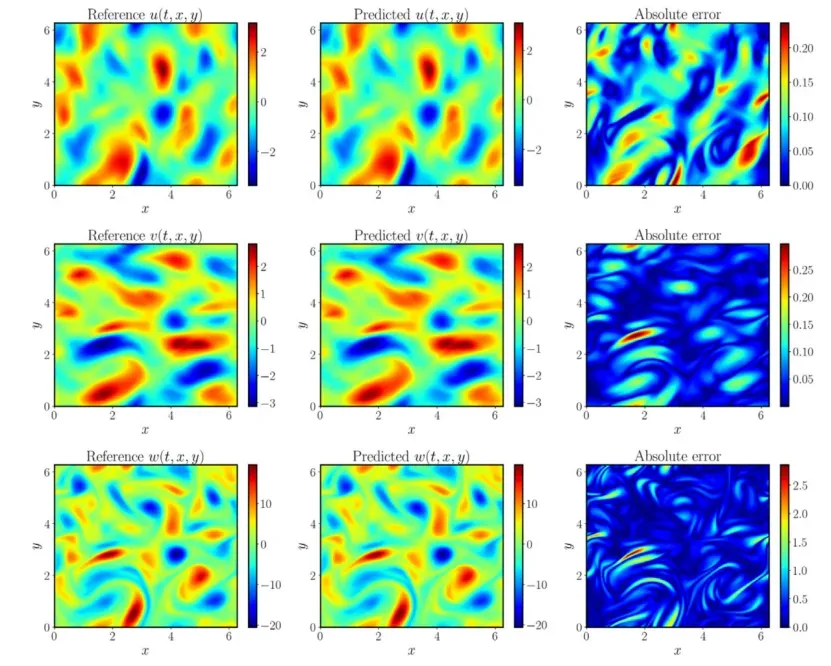
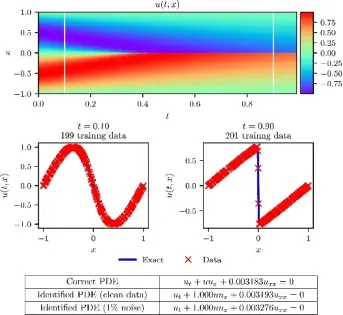
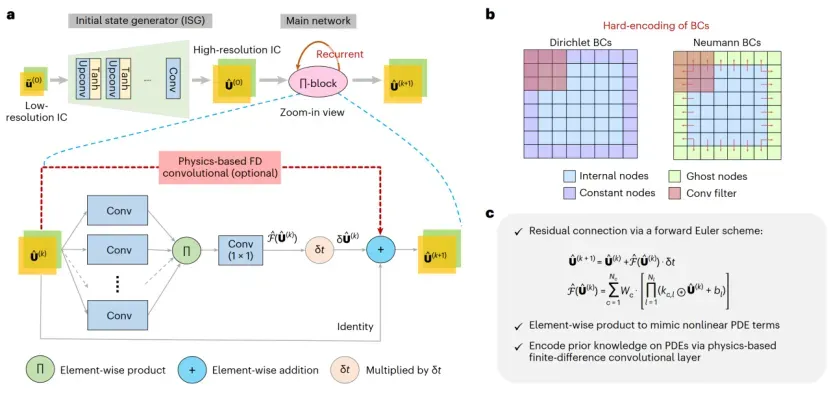
13. 有限差分法转化为神经网络，nature 子刊精讲

Encoding physics to learn reaction–diffusion processes

13.1. 物理编码时空学习

13.2. PDE系统的正演分析

13.3. PDE系统的反演分析

13.4. PeRCNN的结构

13.5. ∏块的普适多项式逼近

13.6. 方程发现与强泛化能力

Day 5 PINN在固体力学中应用 + PINN的库SciANN讲解 + 大模型辅助编程

14. PINN和深度能量法的对比

中科院一区TOP数值计算顶刊Computers and Geotechnics: A Comprehensive Investigation of Physics-Informed Learning in Forward and Inverse Analysis of Elastic and Elastoplastic Footing

15.Footing问题背景与Ritz方法（正问题）

- 问题背景：Footing问题的物理意义与工程应用

- 数学模型：Footing问题的数学描述与控制方程

- Ritz方法：Ritz方法在正演建模中的应用与实现

- PINN框架：论文中PINN实现的核心思路与框架解读

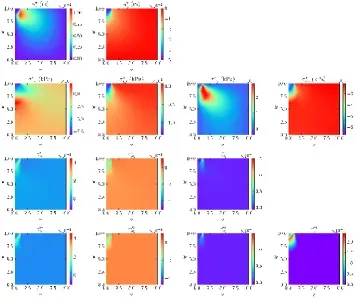
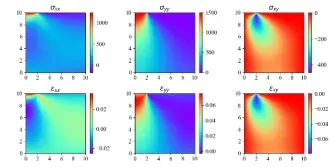
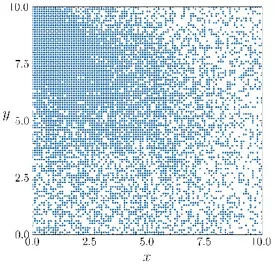
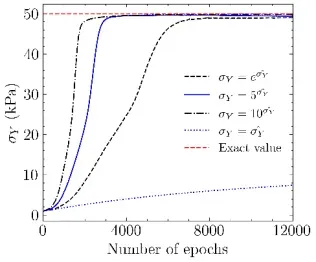
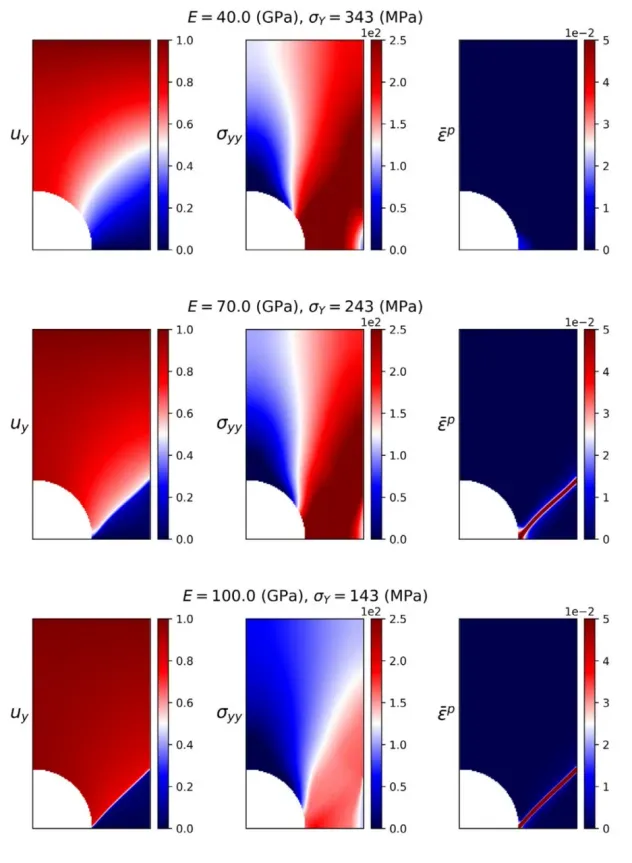
16. Footing问题的逆问题求解

- 损失函数构建：PINN中物理驱动损失函数的设计与实现

- 自适应采样：自适应采样方法的原理与实现细节

- 指数加速：逆问题求解中的指数加速技术

- 代码复现与结果分析：代码实现与结果分析（数据集大小、高斯噪声的影响）

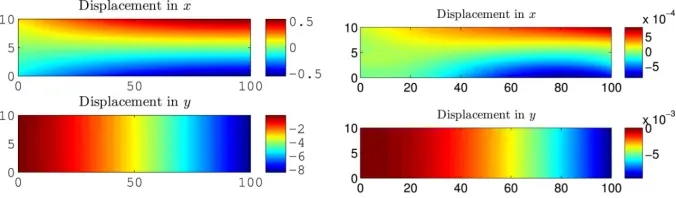
17. JCP顶刊：混合能量法解决固体力学的应力集中问题

计算力学顶刊Journal of Computational Physics：The mixed Deep Energy Method for resolving concentration features in finite strain hyperelasticity

物理知情神经网络（PINN）的引入导致人们对深度神经网络作为固体力学界PDE的通用近似器的兴趣日益浓厚。最近，深能法（DEM）被提出。DEM基于能量最小化原理，与基于PDE残差的PINN相反。DEM的一个显著优点是，与基于强形式残差的公式相比，它需要对低阶导数进行近似。然而，DEM和经典PINN公式都难以解决应力场和位移场的精细特征，例如固体力学应用中的浓度特征。提出了对深能法（DEM）的扩展，以解决有限应变超弹性的这些特征。开发的称为混合深能法（mDEM）的框架引入了应力测量，作为最近引入的纯位移公式的NN的额外输出。使用这种方法，可以更准确地近似Neumann边界条件，并提高通常导致高浓度的空间特征的精度。为了使所提出的方法更加通用，我们引入了一种基于Delaunay积分的数值积分方案，该方案使mDEM框架能够用于具有应力集中的计算域（即具有孔、凹口等的域）通常需要的随机训练点位置集。我们强调了所提出方法的优点，同时展示了经典PINN和DEM公式的缺点。该方法在涉及具有精细几何特征和集中载荷的域的具有挑战性的计算实验的正向计算方面提供了与有限元法（FEM）相当的结果，但还为解决超弹性背景下的逆问题和参数估计提供了独特的能力。

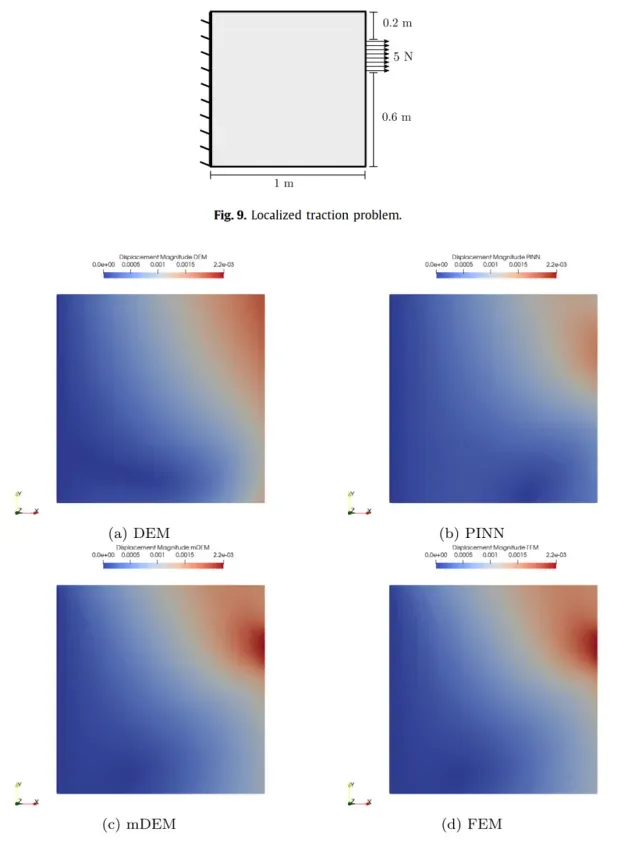
18. PINN库：SciANN讲解与实操

SciANN是一个高级人工神经网络API，使用Keras和TensorFlow后端用Python编写。它的开发重点是实现不同网络架构的快速实验，并强调科学计算、基于物理的深度学习和反演。能够用几行代码开始深度学习是做好研究的关键。

19. DeepSeek、ChatGPT、Grok生成PINN代码解偏微分方程

1 DeepSeek大模型简介

2. DeepSeek大模型生成PINN代码求解椭圆偏微分方程

2.1. Prompt与任务分解

2.2. 代码运行、可视化和Debug

3. ChatGPT大模型生成PINN代码求解抛物偏微分方程

3.1. Prompt与任务分解

3.2. 代码运行、可视化和Debug

4. DeepSeek、Chat GPT、Grok大模型生成PINN代码效果对比

20. 量子计算入门

1 三个基本命题及其拓展

1.1 局部性命题

1.2 概率命题

1.3 邱奇图灵命题

2 双缝干涉实验与几率幅

3 量子比特

4 量子门操作与量子电路

     讲师曾在香港和美国工作和学习，具有计算机和经典数值方法的双重教育背景，在中科院一区Top等计算力学顶刊CMAME以一作发表二十篇SCI论文，包括多篇PINN和传统数值主题的顶刊论文。

2026.1.20---2026.1.23晚上授课(19:00-22:00)

2026.1.24全天授课(上午9:00-11:30下午13:30-17:00)

2026.1.25全天授课(上午9:00-11:30下午13:30-17:00)

2026.1.24---2026.1.25晚上授课(19:00-22:00)

腾讯会议 线上授课（共五天授课时间 提供全程回放视频）

课程费用