【UTD24+代码开源|EV充电调度】从最大流到最优充电:电动汽车调度背后的运筹学逻辑

【正文】

随着电动汽车（EV）的大规模普及，一个看似“工程实现层面”的问题，正逐渐演变为严肃的运筹优化与电力系统挑战：👉 在电网容量受限的情况下，如何为大量电动汽车安排充电，既满足用户需求，又避免功率峰值和能量损耗？

近期，来自**荷兰特温特大学（University of Twente）**的研究团队——Leoni Winschermann、Antonios Antoniadis、Marco E. T. Gerards、Gerwin Hoogsteen 与 Johann Hurink——在运筹学领域顶级期刊 《Operations Research》 发表了一篇极具代表性的工作：

Relating Electric Vehicle Charging to Speed Scaling with Job-Specific Speed Limits

该论文于 2025 年在线发表（Articles in Advance），将 电动汽车充电调度问题 与 经典的速度调度（Speed Scaling）理论 建立了深刻联系，为 EV 充电调度提供了一种结构清晰、可证明最优、计算高效的新思路。

🌍 研究背景｜为什么“聪明充电”这么难？

🔌 现实场景在大型停车场、园区或企业车队中，往往同时接入几十甚至上百辆电动汽车。如果所有车辆“随到随充”，就会带来：

• ⚠️ 变压器过载风险

• 📉 能量损耗显著增加（功率平方/立方相关）

• 🔄 电网运行不稳定

📐 学术挑战从建模角度看，EV 充电问题至少同时具备以下特征：

• ⏱️ 时间约束：每辆车有到达时间、离开时间

• 🔋 能量需求约束：必须在离开前充够电

• 🚘 个体功率上限：不同车辆最大充电功率不同

• 📊 系统目标是“整体功率曲线”，而不是单车最优

传统方法多采用：

• 数学规划（LP/QP）

• MPC（模型预测控制）

• 启发式或规则法

👉 问题在于：这些方法往往没有利用问题的内在结构，难以解释“为什么这样充是最优的”。

✨ 研究亮点｜把 EV 充电“翻译”为速度调度问题

这篇论文最精彩的地方，在于它做了一件非常“运筹”的事情：

💡 把 EV 充电调度，等价映射为“带作业速度上限的速度调度问题”(Deadline-based Speed Scaling with Speed Limits, DSL)。

🔁 关键对应关系

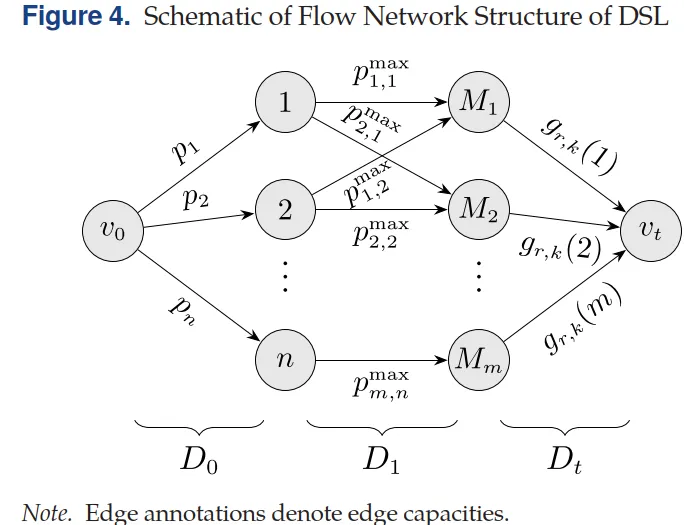
在此基础上，作者提出了一个核心算法：

🚀 FOCS：Flow-based Offline Charging Scheduler

🔹 核心思想：

• 将时间划分为“原子区间”

• 构建 最大流网络

• 通过 多轮 max-flow，逐步识别“关键时间段（critical intervals）”

• 在这些时间段内，功率水平不可再降低

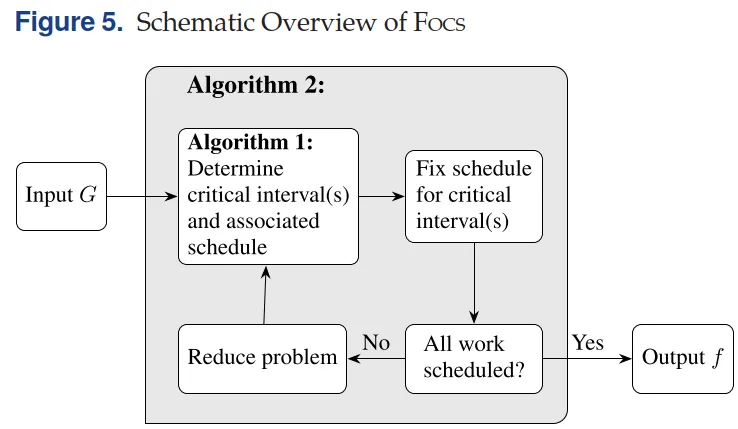
🔹 理论优势：

• ✅ 全局最优（严格凸目标）

• ✅ 给出 KKT 最优性条件

• ✅ 证明调度结构的唯一性（功率曲线）

🔹 在线情形下，作者还分析了Average Rate (AVR) 算法和Optimal Available (OA) 算法，并给出了**竞争比（competitive ratio）**的严格上界。

📊 数值实验｜400 辆车，只要 2.5 秒

理论之外，作者使用真实 EV 充电数据进行了大量数值实验，结果非常“工程友好”：

⚙️ 实验规模

• 🚗 最多 400 辆 EV

• ⏲️ 时间分辨率：15 分钟

📈 FOCS 算法算得快吗？

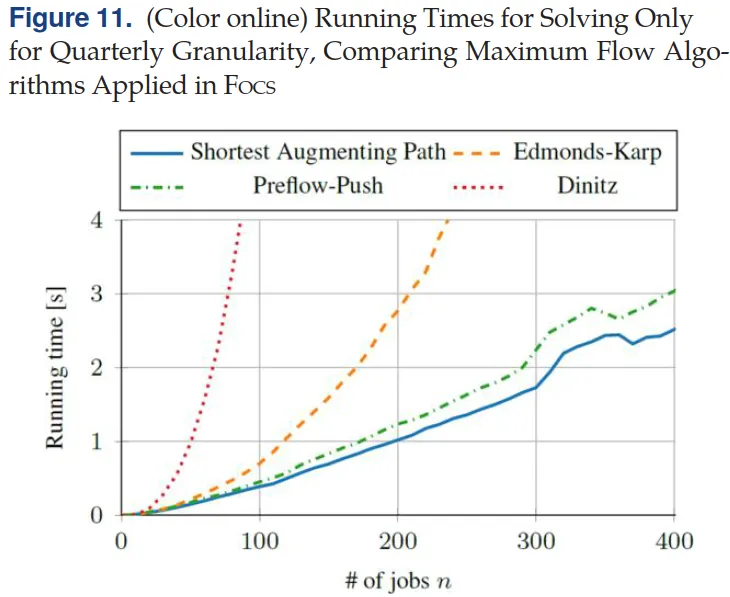
作者首先测试了 FOCS 在不同最大流算法实现下的实际运行时间，结果如图 11 所示。实验发现，不同最大流算法对 FOCS 的计算效率影响非常明显：

• 使用 shortest augmenting path 方法时，FOCS 的运行时间在 EV 数量增加到 400 辆之前，整体增长趋势接近线性，计算效率较高；

• 相比之下，Edmonds–Karp 和 Dinitz 方法的运行时间随问题规模增长更快，在较大规模下出现明显的非线性增长；

• Preflow–push 方法的表现与 shortest augmenting path 类似，同样能够保持较好的计算效率。

总体来看，数值结果表明：在合理选择最大流算法的前提下，FOCS 可以在真实规模的电动汽车充电调度问题中高效运行，具备实际应用潜力。

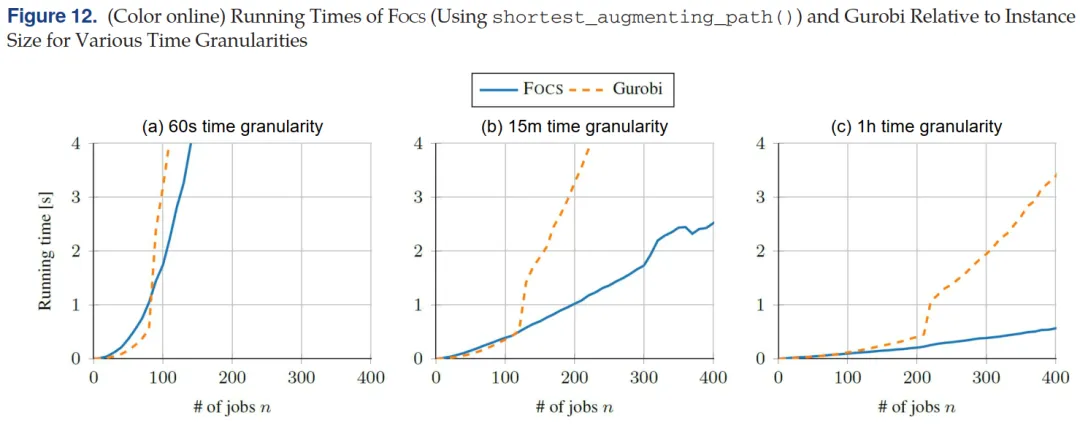
📊 FOCS 与商用求解器 Gurobi 的对比

在数值实验中，作者进一步将 FOCS 与商用优化求解器 Gurobi 进行了对比。图 12 展示了在 不同时间粒度（1 分钟、15 分钟、1 小时） 下，两种方法的运行时间随 EV 数量变化的情况。

实验结果可以总结为几个直观结论：

• 在 问题规模较小 时，Gurobi 求解的二次规划问题运行速度与 FOCS 相当，部分情况下甚至略快；

• 但随着 EV 数量增加，Gurobi 的运行时间增长明显更快，而 FOCS 的运行时间增长趋势相对平缓；

• 因此，当问题规模达到一定水平后，FOCS 在运行时间上开始明显优于 Gurobi：

• 约 90 辆 EV（1 分钟粒度）

• 约 120 辆 EV（15 分钟粒度）

• 约 80 辆 EV（1 小时粒度）

⚠️ 一个有意思的现象

图 12 还显示，在较大规模实例下，Gurobi 的运行时间会出现突然陡增。作者指出，这种现象可能与内存使用达到某一阈值有关，从而导致求解效率急剧下降。

相比之下，FOCS 的运行时间整体表现更加稳定，在大多数实验规模下呈现接近线性的增长趋势。

⏱ 一个直观对比数字

为了给读者一个更直观的感受，作者给出了如下对比：

• 在 1 分钟时间粒度、400 辆 EV 的情况下：

• FOCS：约 36 秒

• Gurobi：约 62 秒

而在实际工程中更常用的 15 分钟时间粒度下，FOCS 对 400 辆 EV 的调度仅需约 2.5 秒（中位数）。

📊 在线算法 AVR 与 OA 的实际表现

需要指出的是，FOCS 是一种离线最优算法，依赖于对所有车辆到达与离开信息的完全掌握。然而，在实际电动汽车充电场景中，未来车辆信息往往不可预知。因此，作者进一步对两种经典在线算法 Average Rate（AVR） 和 Optimal Available（OA） 进行了仿真评估，并以 FOCS 的最优解作为性能基准，以量化“信息不完全”所带来的性能损失。

图 13 展示了在 500 个真实数据实例中，在线算法 AVR 和 OA 相对于离线最优解 FOCS 的实际性能表现。结果表明，两种在线算法在真实场景下的性能损失远小于其理论最坏情况，其中 OA 的整体表现优于 AVR。

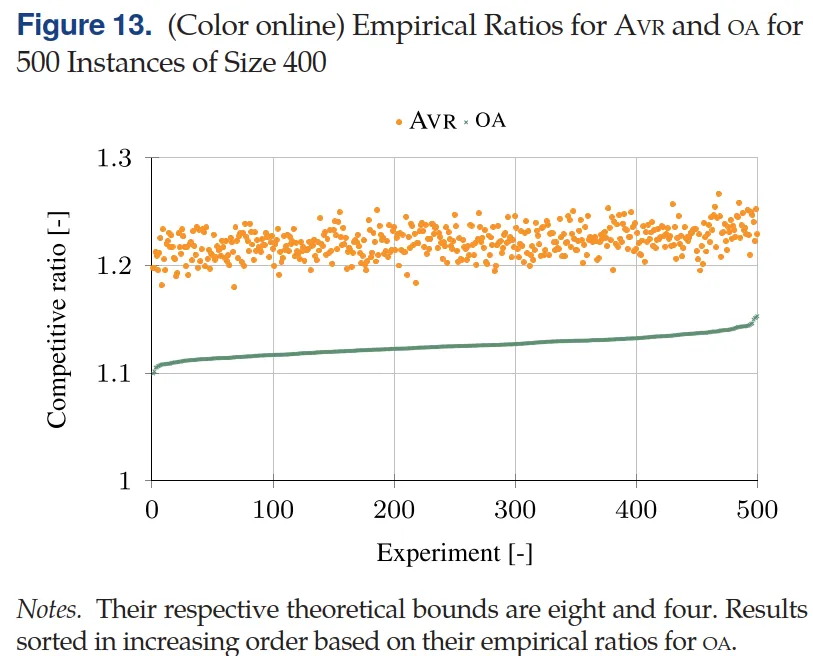
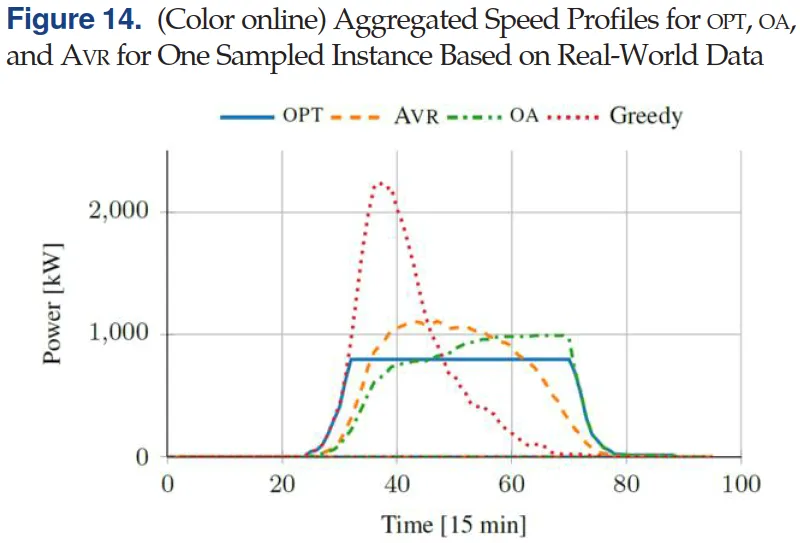
图 14 对比了一个代表性实例中，不同算法得到的聚合充电功率曲线。FOCS 产生最平滑、能耗最低的曲线，AVR 充电过程更均匀，而 OA 更倾向于将负荷推迟到后段；无控制策略 则产生明显的功率峰值。整体来看，AVR 和 OA 均显著优于无控制的贪婪充电策略。

代码开源：

https://pubsonline.informs.org/doi/suppl/10.1287/opre.2024.1044

🧭 结语｜为什么这篇文章值得反复读？

从科研视角看，这篇工作至少有三点启示：

🔹 1️⃣ 问题建模比算法本身更重要EV 充电 ≠ 简单的功率分配，而是一个深度结构化的调度问题。

🔹 2️⃣ 运筹学经典理论依然“宝刀未老”Speed Scaling、最大流、KKT 条件，在新能源系统中焕发新生命。

🔹 3️⃣ 为未来研究打开接口

• EV + 可再生能源

• EV  车队 +微电网

• 在线调度 + 不确定性

📌 如果你从事：

• 电动汽车充电调度

• 综合能源系统

• 运筹优化与算法设计

这篇论文，非常值得精读。

注：素材来源于网上公开开源内容。如有侵权，随时可删。本文编辑过程借助ChatGPT润色。如需了解更多内容，请访问（点击阅读原文）：https://pubsonline.informs.org/doi/full/10.1287/opre.2024.1044

扫码关注！

一个智慧交通与能源前沿动态与科研资源平台