1.前言
斯塔克尔伯格(Stackelberg)定价博弈是一种经济学中的博弈模型,常用于描述市场中的价格竞争。在斯塔克尔伯格定价博弈中,假设有两个参与者,一个是领先者(leader),另一个是追随者(follower)。领先者首先决定价格,而追随者在得知领先者的价格后再做出自己的定价。这种顺序决策的特点使得领先者可以考虑追随者的反应,并相应地制定策略。在斯塔克尔伯格定价博弈中,领先者通常会优先考虑自身利益最大化,而追随者则会根据领先者的定价做出反应。领先者的目标是通过定价策略来最大化自己的利润,而追随者的目标是尽可能减少自己的损失。当博弈为非完美信息博弈时,参与者并不拥有完全的信息,即参与者在博弈中可能只能观察到有限的信息或仅能推测对手的策略和信息。因此博弈中,每个参与者会根据自己所观察到的信息做出决策。这些信息可以是对手的先前行动、信号、观察结果等。参与者需要基于有限的信息,通过推断和预测对手的策略来制定自己的最优策略。常见的 Follower 策略包括:- 反应函数策略(Reaction Function Strategy):Follower 基于 Leader 的定价策略制定自己的反应函数,反映了对 Leader 定价的最佳响应。Follower 根据 Leader 的定价水平来确定自己的最优定价或市场行为。- 跟随策略(Follow-the-Leader Strategy):Follower 在市场中采取与 Leader 相同的定价策略,即跟随 Leader 的定价水平。这种策略假设 Follower 认为 Leader 的定价是最优的,并试图通过跟随 Leader 来获得最大化的利润。- 入侵策略(Incumbent Strategy):Follower 选择进入市场并与 Leader 进行价格竞争。Follower 通过以低于 Leader 的价格销售产品或提供更多的附加服务来吸引消费者,从而争夺市场份额。- 不合作策略(Non-cooperative Strategy):Follower 采取独立的定价策略,不考虑 Leader 的定价策略。Follower 可能通过制定自己的价格战略来最大化自身的利润,而不受 Leader 的影响。
2.博弈规则
设Leader的定价策略为,Follower的定价策略为,且有:(1)Leader策略空间为;(2)市场需求(价格-销售量)与双方定价的关系模型为;(3)Leader每日利润与双方定价的关系为,其中单位成本;(4)Leader完全不了解Follower的策略空间、定价策略和每日利润,即博弈对于Leader来说是非完美信息,但是Leader可以获取过去100天内Follower的定价数据,因此可以对Follower策略进行预测。Leader的博弈目标为最大化接下来30天内的累积利润。(5)设整个周期内(130天内)Leader的单位成本,策略空间和市场需求模型不变。
博弈流程为:在第天,Leader首先给出定价。在知晓Leader定价后,Follower随后给出自己的定价,其中。Leader可以获取天内的数据来帮助自己最大化内的累积利润,即最大化。Follower的策略和每日利润能随时间变化。
3.Leader最优策略求解
根据最优性原理,最大化101-130这30天内Leader的累积利润等于最大化其中每天的利润,即求解以下最优化问题
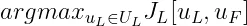 (1)
(1)
其中
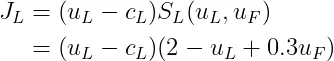 (2)
(2)
实际上就是求关于的最大值。根据函数最大值的求法,即求使
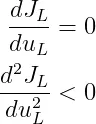 (3)
(3)
4.Follower策略预测
如果Leader能预测关于的关系函数,则可将转换成的函数,从而求解Leader的最优策略。因为1-100天内的历史数据已知,则预测目标就是从历史数据中学习follower策略的一个近似函数。这里采用计算速度和精度都比较好的递推最小二乘法(Recursive Least Square Algorithm)。若已知前T个时刻的数据点,设第k个时刻的数据点,设回归模型为
(4)
其中维度为,为自变量个数。为回归系数,其维度为。因为回归模型是时变的,所以回归系数需要随时间更新,更新方程如下:
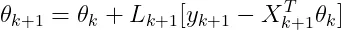 (5)
(5)
其中
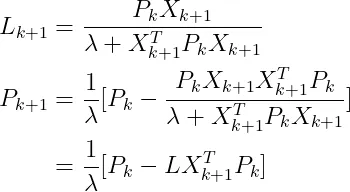 (6)
(6)
另外,还需要确定初始条件,即确定和才能更新,这里采用简单初始条件法(Simple initial condition),令
(7)
上式中为一个大的常数,一般取,为单位向量,维度为。为的一个猜测值。则的预测值可以表示为
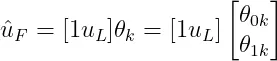 (8)
(8)
则根据式有
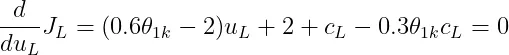 (9)
(9)
解得Leader最佳策略为
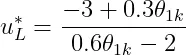 (10)
(10)
5.实验结果
取新旧平滑因子,让Leader 分别与三个采用不同策略的玩家、和进行博弈,结果如下。
5.1 策略学习结果
(1)
(2)
(3)
5.2 双方博弈结果
第101-130天的博弈结果如下:(1)Leader每日利润曲线
预测结果:
(2)Leader每日利润曲线:
预测结果:
(3)Leader每日利润曲线:
预测结果: